多目标优化遗传算法综述

Multi-objective optimization using genetic algorithms: A tutorial. Abdullah Konak, et al.

帕累托最优理论

在数学上，多目标优化问题可以被公式化为如下表述：
如果多目标问题的每一种解都可以使用\(n\)维空间\(X\)中的一个的向量进行表示：\(\boldsymbol{x}=\{x_1,x_2,...,x_n\}\)，那么多目标优化就是找到一个解\(\boldsymbol{x^*}\)使得\(K\)个目标函数(objective function)\(z_i(\boldsymbol{x})\)具有最小值:
\[z(x^*)=\{z_1(\boldsymbol{x^*}),z_2(\boldsymbol{x^*}),...,z_n(\boldsymbol{x^*})\}\]

同时，搜索空间\(X\)受到一系列的约束条件(constrain)\(g\)的限制：\(g_j(\boldsymbol{x^*})=b_j\)，\(j=1,...,m\).

实际情况是，许多约束的满足条件彼此之间会冲突，因此实际上想要找到一个多目标解使得所有目标函数同时达到最优解几乎是不可能的。因此，事实上多目标优化是寻找一组最优化的近似解，这个解在每一个目标函数中的结果都在可以接受的范围内，而且没有其他的解可以比这个解至少在一个目标函数中更好。

支配和帕累托最优解

假设优化问题为最小值优化，如果一个解\(\boldsymbol{x}\)至少在一个目标函数中的结果比另一个解\(\boldsymbol{y}\)好：\(z_i(\boldsymbol{x})<z_i(\boldsymbol{y}), i=1,2,...,K\)，且在其他目标函数中的结果不比\(\boldsymbol{y}\)差：\(z_j(\boldsymbol{x})≤z_j(\boldsymbol{y}),j=1,2,...,K\)，那么称解\(\boldsymbol{x}\)支配(dominate)另一个解\(\boldsymbol{y}\)(\(\boldsymbol{x}≻\boldsymbol{y}\)).
进一步地，如果一个解\(\boldsymbol{x}\)在搜索空间中不被其他任何一个解支配，那么这个解被称为帕累托最优解(Pareto optimal，以下简称帕累托解)或者帕累托效率(Pareto efficiency)。

在搜索空间中存在多个帕累托最优解，比如对于目标函数\(f_1(x),f_2(x)\)，\([1,2]\)和\([2,1]\)相互之间不被支配。

所有的帕累托最优解构成的集合称为帕累托最优解集合(Pareto optimal set)，这些帕累托最优解带入到每一个目标函数中得到的结果所构成的集合称为帕累托前沿(PF, Pareto Front).

因此，多目标优化的关键是在于找到帕累托最优解集合。
但是，随着搜索空间\(X\)维度的升高，帕累托集合的数量会越来越大。对于大多数问题而言，帕累托解的数量巨大甚至是无穷多的。实际要想找完所有的帕累托最优解是不可能的。并且证明这些解的最优性在计算上也是无法实现的。因此实际的多目标优化是找到最接近全解的帕累托最优解集合。要想逼近完整的帕累托最优解集合，最优化算法需要尽可能地达到三个相互制约的目标：

1. 找到的帕累托前沿的近似需要尽可能地接近多目标问题真正的帕累托前沿。
   
2. 找到的帕累托近似最优解集合中，解在搜索空间中的分布是尽可能均匀的，如此近似最优解的集合中的解具有丰富的多样性，不会偏向于任何一个特定的目标函数而是整体地达到近似最优。这样可以让决策者无偏地在这些帕累托解中权衡。
   
3. 找到的帕累托前沿的近似需要尽可能的捕捉真正帕累托前沿的分布特性。也就是说，最优化算法需要尽可能的找到帕累托最优解集合中那些可能分布在搜索空间角落的极端帕累托解。

对于给定的计算和时间限制，第一个目标可以通过将搜索聚焦在帕累托前沿的某一个部分达成；但是相对地，第二个目标要求算法的搜索需要均匀无偏；第三个目标要求算法尽可能地扩展已经找到的帕累托前沿的两侧，继续寻找新的解。

多目标遗传算法

遗传算法(Genetic Algorithm)相比于其他的经典算法在多目标优化问题上的优点主要如下：
- 由于遗传算法是一种基于群体的搜索优化算法，它可以在一次运行中产生多个帕累托解，而类似于神经网络的算法则需要多次运行才能够生成足够的帕累托解。^{<span class="hint--top hint--rounded" aria-label="C. A. C. Coello, "Evolutionary multi-objective optimization: a historical view of the field," IEEE Computational Intelligence Magazine, vol. 1, no. 1, pp. 28-36, 2006, doi: https://doi.org/10.1109/MCI.2006.1597059.">[1]}
- 相较于其他算法，遗传算法本身的搜索能力对帕累托前沿的形状不敏感。^{<span class="hint--top hint--rounded" aria-label="C. A. C. Coello, "Evolutionary multi-objective optimization: a historical view of the field," IEEE Computational Intelligence Magazine, vol. 1, no. 1, pp. 28-36, 2006, doi: https://doi.org/10.1109/MCI.2006.1597059.">[1]}
- 面对不同的目标函数，遗传算法可以通过交叉不断发掘新的帕累托解以延伸已经发现的帕累托前沿近似。
- 大多数时候，多目标的遗传算法不需要对目标确定优先级(prioritize)、缩放(scale)、或者设置权重(weight)。

综上所述，使用遗传算法对多目标问题进行优化已经成为一种流行的使用方法。第一个多目标遗传算法(Multi-objective GA)是由Schaffer提出的VEGA(Vector Evalutated GA). 之后陆陆续续有更多的遗传算法的改进被应用于多目标优化中，它们的评述在文中总结在本文文末。

多目标遗传算法的设计

适应度函数

线性组合和赋权

最经典的一种设计多目标遗传算法适应度函数的方法是将所有的适应度函数进行线性组合，并分别赋予权重\(w_i\)。如此多目标优化将通过线性组合转化为一种近似于单目标优化问题的求解方式：
\[min [z] = w_1z_1(\boldsymbol{x})+w_2z_2(\boldsymbol{x})+...+w_kz_k(\boldsymbol{x})\] 通常所有的权重和为1：\(∑w_i=1\)。这种方法通常需要使用者通过某种方式给出权重\(\boldsymbol{w_i}=\{w_1,w_2,...,w_k\}\)，常见的赋权方式为按照优先级赋权，因此这种方法被称为优先级方法(priori approach)。
在这种方法下，算法需要使用不同的权重多次运行进行测试，如何设置不同的权重是该方法中的一个重要问题。WBGA中使用了一种自动化赋权的方式：WBGA中，权重与个体的染色体绑定，跟随个体一同被选择和进化。 另一种基于MOGA的多目标遗传算法RWGA则在选择阶段为每一个个体使用随机生成的不同的权重向量\(\boldsymbol{w_i}\)。使用随机赋权的目的是通过随机的权重可以在一次算法运行中规定不同的搜索方向而不需要添加和设置其他参数。

Procedure RWGA:
\(E\): external archive to store non-dominated solutions found during the search so far;
\(n_E\): number of elitist solutions immigrating from \(E\) to \(P\) in each generation.

• Step 1: Generate a random population.
  
• Step 2: Assign a fitness value to each solution \(x∈P_t\) by performing the following steps:
  • Step 2.1: Generate a random number uk in \([0,1]\) for each objective \(k, k=1,...,K\).
    
  • Step 2.2: Calculate the random weight of each objective \(k\) as \(w_k=(1/u_k)\sum_{i=1}^Ku_i\).
    
  • Step 2.3: Calculate the fitness of the solution as \(f(\boldsymbol{x})=\sum_{i=1}^Kw_kz_k(\boldsymbol{x})\).
• Step 3: Calculate the selection probability of each solution \(x∈P_t\) as follows: \(p(\boldsymbol{x})=(f(\boldsymbol{x})-f^{min})^{-1}\sum_{\boldsymbol{y}∈P_t}(f(\boldsymbol{y})-f^{min})\)
  where \(f^{min}=min\{f(\boldsymbol{x})|\boldsymbol{x}∈P_t\}\).
  
• Step 4: Select parents using the selection probabilities calculated in Step 3. Apply crossover on the selected parent pairs to create \(N\) offspring. Mutate offspring with a predefined mutation rate.
  Copy all offspring to \(P_{t+1}\).
  Update \(E\) if necessary.
  
• Step 5: Randomly remove nE solutions from \(P_{t+1}\) and add the same number of solutions from \(E\) to \(P_{t+1}\).
  
• Step 6: If the stopping condition is not satisfied, set \(t=t+1\) and go to Step 2. Otherwise, return to \(E\).

线性组合的主要优点是这种方法非常简单而且易于实现。相对地，线性组合的方式查找对非凸的目标函数性能较差。因此，如果真正的帕累托前沿是非凸函数，按照线性组合并不能完全找到帕累托最优解，而且找到的最优解很难做到均匀分布。

改变目标函数

在最初的多目标遗传算法VEGA中，使用了另一种适应度函数。VEGA根据目标函数的个数将整个种群分成了若干个子种群:\(P_1,P_2,...,P_K\)。每个子种群\(P_i\)对应一个特定的目标函数\(z_i\)，每一代中按照该目标函数赋予适应度、进行选择后再综合进行交叉和变异等遗传操作。

Procedure VEGA:
\(N_S\): subpopulation size (\(N_S=N/K\)).
- Step 1: Start with a random initial population \(P_0\). Set \(t = 0\).
- Step 2: If the stopping criterion is satisfied, return \(P_t\). - Step 3: Randomly sort population \(P_t\).
- Step 4: For each objective \(k, k= 1,...,K\), perform the following steps:
- Step 4.1: For \(i = 1+(k-1)N_S, ... ,kN_S\), assign fitness value \(f(\boldsymbol{x}_i) = z_k(\boldsymbol{x}_i)\) to the ith solution in the sorted population.
- Step 4.2: Based on the fitness values assigned in Step 4.1, select \(N_S\) solutions between the \((1+(k-1)N_S)\)th and \((kN_S)\)th solutions of the sorted population to create subpopulation \(P_k\).

• Step 5: Combine all subpopulations \(P_1,...,P_k\) and apply crossover and mutation on the combined population to create \(P_{t+1}\) of size \(N\). Set \(t = t + 1\), go to Step 2.

这种方法主要的优点是易于实现，而且VEGA的计算效率几乎和单目标遗传算法相同。事实上除了评估一步，其余步骤VEGA的行为和单目标传统遗传算法是相同的。
不过，种群对于不同的目标函数的敏感程度不同，也就是说，不同目标函数主导进化方向的能力是不同的，且在VEGA这样的方法中存在竞争关系。因此种群的进化方向可能会偏向于其中一个对其敏感的目标函数，对其他目标函数的收敛性相对更差。

帕累托排序

帕累托排序(Pareto ranking)利用了帕累托最优理论中“支配”的概念来为不同的个体赋予适应度。简单来说，种群中的个体适应度表示为排序。具有更高支配地位的个体会具有更好的适应度。在本文中，越好的个体具有更低的适应度，排名更小更靠前。
Goldberg ^[2] 提出了第一种帕累托排序方法，简单来说就是对于当前种群中的所有个体，选择出其中的帕累托解并移入另一个列表中，然后再筛选剩余个体中的新的帕累托解。（即去掉上一次的帕累托解后现有集合中新的不受其他种群支配的个体），如此往复。
其过程详细描述如下：
- Step 1: Set \(i=1\) and \(TP=P\).
- Step 2: Identify none-dominated solutions in \(TP\) and assigned them set to \(F_i\).
- Step 3: Set \(TP=TPF_i\). If \(TP=∅\) go to Step 4, else set \(i=i+1\) and go to Step 2.
- For every solution \(\boldsymbol{x}∈P\) at generation \(t\), assign \(r(\boldsymbol{x},t)=i\text{ if }\boldsymbol{x}∈F_i\).

如此排序的结果最终会生成若干个具有支配层级关系的每次基于当前个体集合的帕累托前沿\(F_1,F_2,...\)，称为非支配前沿(none-dominated fronts). \(F_1\)是当前种群中所有个体的帕累托前沿。
并且可以发现，\(F_i\)的支配程度要高于\(F_{i+1}\)中的个体。NSGA使用了这种排序方法，并且还是用了冗余的适应度(dummy fitness)使得\(F_i\)中最差个体的适应度/排名仍然优于\(F_{i+1}\)中最好个体的适应度/排名。
在NSGA-II中使用了更快速的帕累托排序算法，每个个体的排名表示如下：
\[r(\boldsymbol{x},t)=1+nq(\boldsymbol{x},t)\] 其中\(nq(\boldsymbol{x},t)\)表示的是第\(t\)代中个体\(\boldsymbol{x}\)受支配的个体数。\(\boldsymbol{x}\)被越多的个体支配，其适应度越差。
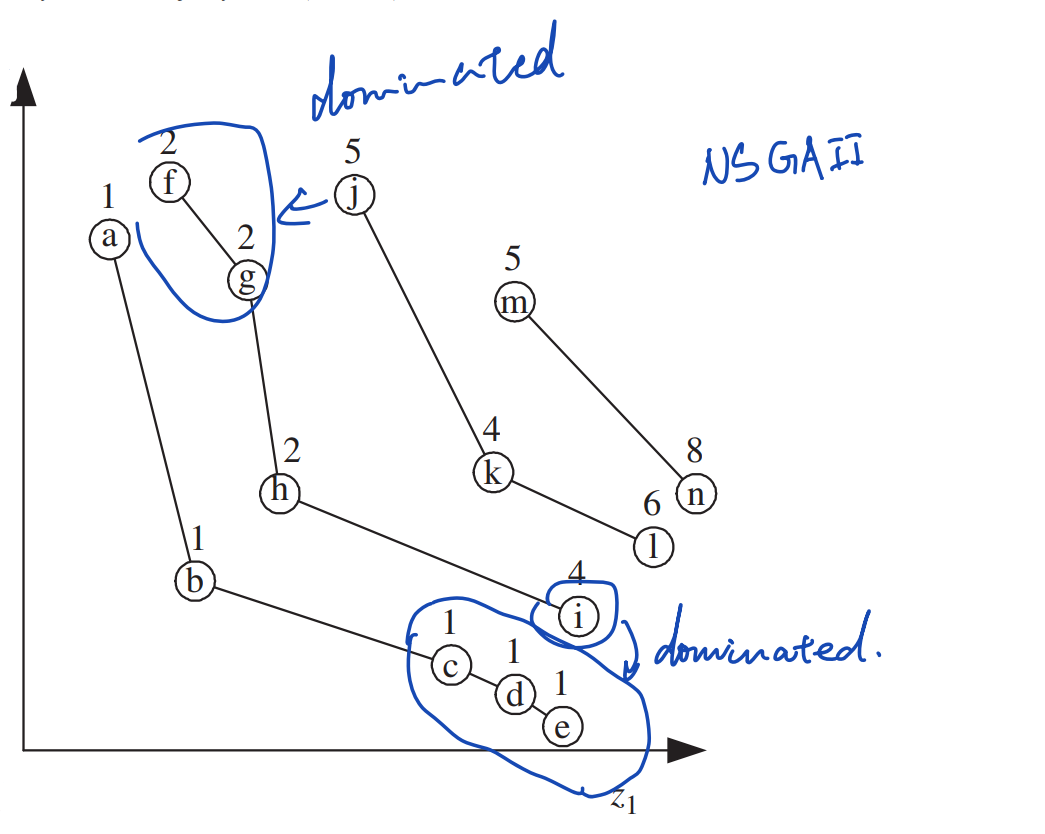
可以发现，这种排名的设置惩罚了在帕累托前沿近似密集区域的个体。比如下图中个体\(i\)的排名要低于同一个非支配前沿\(F_2\)的其他个体\(f,g,h\)，因为\(i\)受到更多的个体支配。这表示支配\(i\)的个体\(c,d,e\)在上一个非支配前沿\(F_1\)中是紧密分布的。

SPEA增添了一个外置列表\(E\)用于存储历史上所有的非支配个体。对于在\(E\)中的每一个个体\(\boldsymbol{y}∈E\)，定义：
\[s(\boldsymbol{y},t)=\frac{np(\boldsymbol{y},t)}{N_P+1}\] 其中\(np(\boldsymbol{y},t)\)是第\(t\)代，种群\(P\)中\(\boldsymbol{y}\)支配的个体数量。现有种群\(P\)中个体\(\boldsymbol{x}∈P\)的排名表示为\(\boldsymbol{x}\)受支配的每一个\(\boldsymbol{y}\)的\(s\)之和：
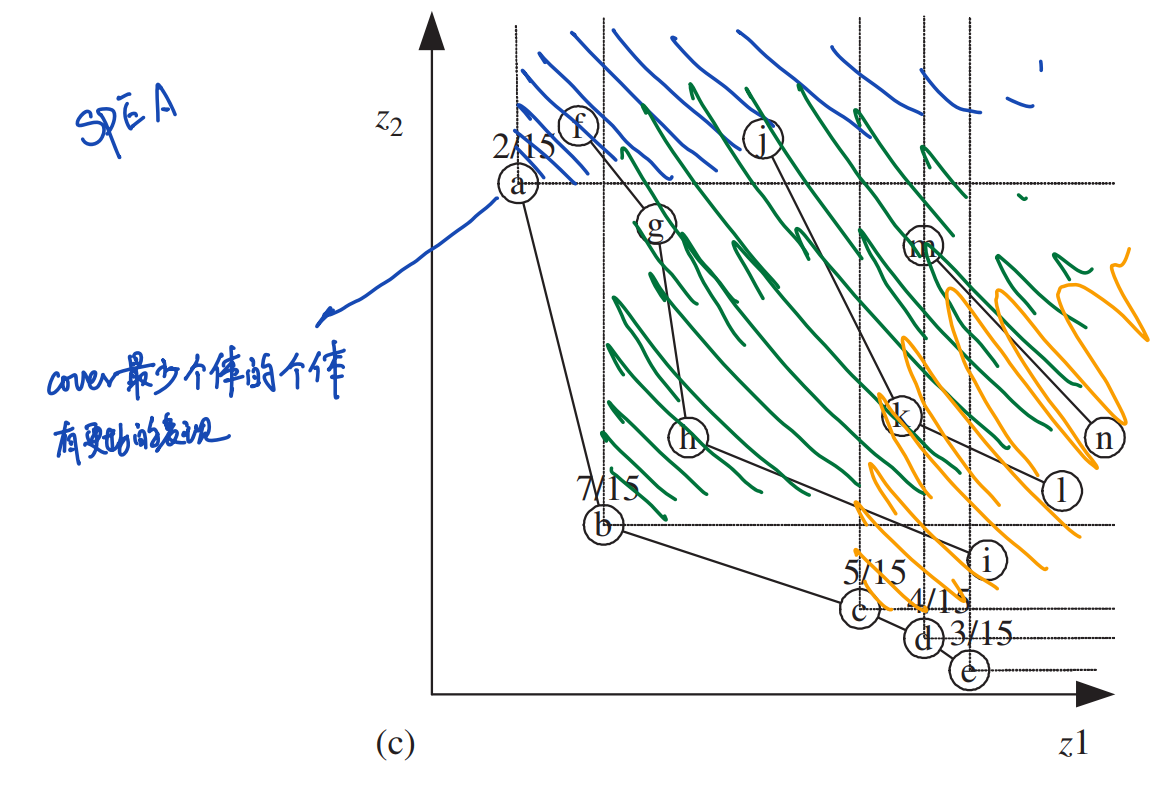
\[r(\boldsymbol{x},t)=1+\sum_{\boldsymbol{y}∈E,\boldsymbol{y}≻\boldsymbol{x}}s(\boldsymbol{y},t)\] 这种排名下，支配越少个体的非支配解具有更优的适应度，使得整个帕累托前沿中的帕累托解更容易分布均匀。
比如下图中的个体\(a\)就具有更优的适应度，因为它在15个个体中只支配了2个个体。而\(b\)支配了7个个体，\(c,d,e\)分别支配了5，4，3个个体。

积累排序密度策略

积累排序密度策略(Accumulated Ranking Density Strategy)同样旨在惩罚稠密区的个体，其中的排名表示为：
\[r(\boldsymbol{x},t)=1+\sum_{\boldsymbol{y}∈P,\boldsymbol{y}≻\boldsymbol{x}}r(\boldsymbol{y},t)\] 这种排名避免了使用外置列表\(E\)。但是，其排名计算存在先后顺序：要想计算\(\boldsymbol{x}\)的排名，就必须先求出支配\(\boldsymbol{x}\)的全部个体\(\boldsymbol{y}\)的排名。
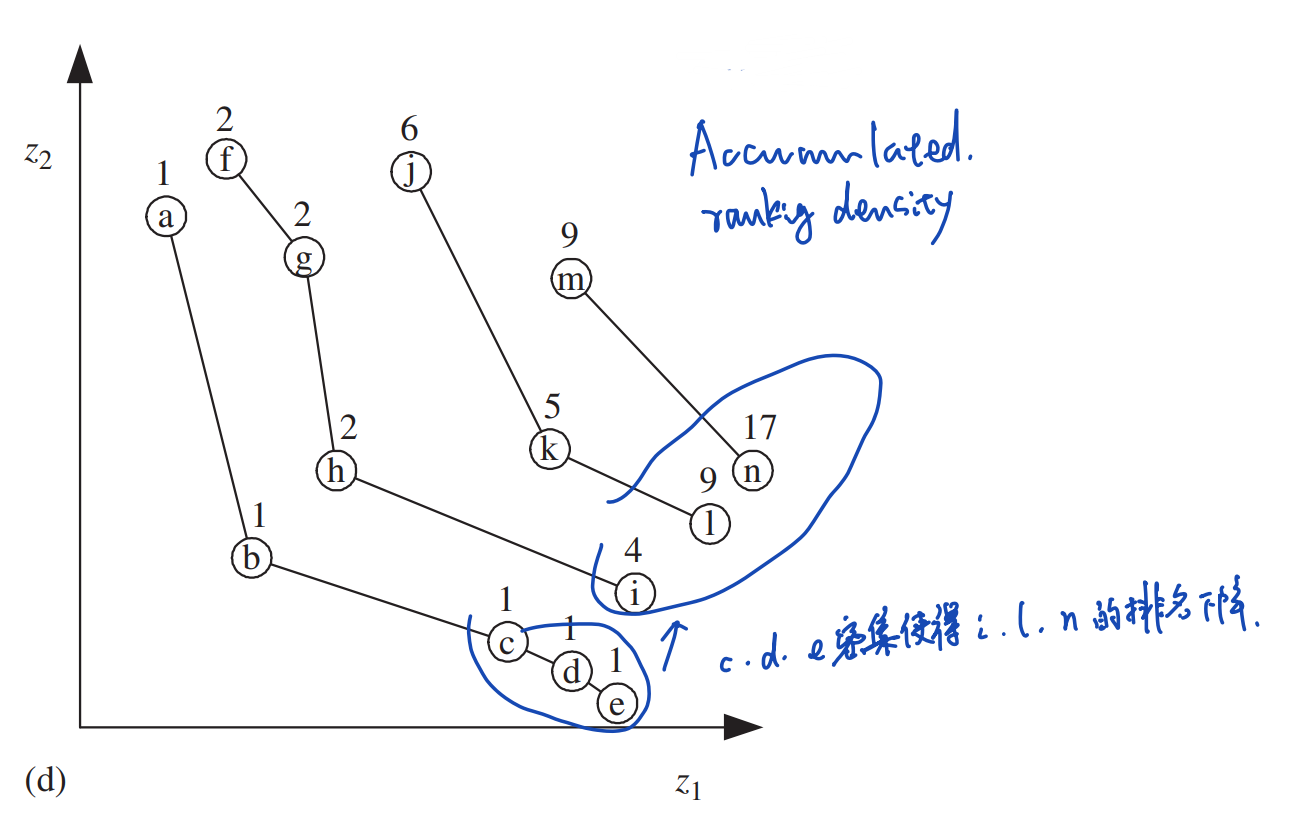
在这种排名下，受到之前非支配前沿中稠密个体支配的个体在本非支配前沿中具有更差的适应度。比如下图中受到\(F_1\)中个体\(c,d,e\)支配的个体\(i,l,n\)在它们各自的非支配前沿中都具有更低的排名。

总而言之，上述的排序策略得到的排名都可以直接作为个体的适应度进行使用。它们通常结合下面提到的适应度共享(fitenss sharing)方法来得到更为广泛和均匀的帕累托前沿近似 （满足目标2和3）。

多样性：适应度共享和小生境

为了要得到均匀分布的帕累托前沿近似，始终保证当前种群中的解要具有多样性，即涵盖帕累托前沿的不同区域。如果没有采取保护种群多样性的方法，种群总是倾向于形成若干个内部个体彼此相似的子种群，这种现象成为基因漂变(Genetic Drift)。这些子种群被称为小生境(niche)。有如下的方式可以解决基因漂变的问题。

适应度共享

适应度共享(fitness sharing)的目的是为了找到没有探索过的帕累托前沿的部分，同时减少帕累托前沿稠密区（dense area, 指个体分布非常密集的区域）个体的适应度，它通常通过设置惩罚函数(penalty function)来降低（或者称为惩罚）那些位于稠密区个体的适应度。要做到这一点，就必须要给出明确的对于稠密的定义。
Fonseca和Fleming使用了一种类似于归一化的欧氏距离来衡量个体之间的距离，并根据此来给出对稠密的定义。在他们提出的方法中，现有种群中的每个个体都与其他所有个体两两配对一次，在每个配对中，个体\(\boldsymbol{x}\)和\(\boldsymbol{y}\)的距离表示为：
\[dz(\boldsymbol{x},\boldsymbol{y})=\sqrt{\sum_{k=1}^K\left(\frac{z_k(\boldsymbol{x})-z_k(\boldsymbol{y})}{z_k^{max}-z_k^{min}}\right)^2}\] 其中\(z_k^{max}\)和\(z_k^{min}\)分别是迄今为止被探索到的目标函数\(z_k(·)\)的最大值和最小值。
对个体\(\boldsymbol{x}\)其适应度\(f(\boldsymbol{x},t)\)会被附近的个体稀释：
\[f'(\boldsymbol{x},t)=\frac{f(\boldsymbol{x},t)}{nc(\boldsymbol{x},t)}\] 其中\(nc(\boldsymbol{x},t)\)被称为\(\boldsymbol{x}\)的小生境距离(niche count)：
\[nc(\boldsymbol{x},t)=\sum_{\boldsymbol{y}∈P,r(\boldsymbol{y},t)=r(\boldsymbol{x},t)}max\left\{\frac{σ_{share}-dz(\boldsymbol{x},\boldsymbol{y})}{σ_{share}},0\right\}\] 其中\(σ_{share}\)是一个预先决定的参数，称为小生境大小，决定了需要考虑的个体范围。 如此，\(nc(\boldsymbol{x},t)\)越大，\(\boldsymbol{x}\)附近越稠密，\(f'(\boldsymbol{x},t)\)越小。

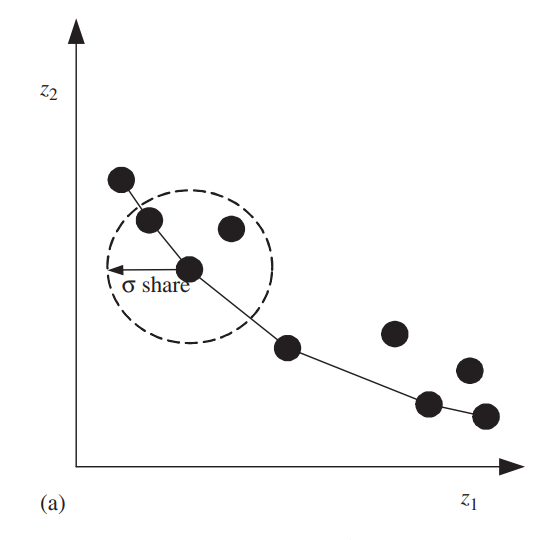
因此，小生境限制了查找个体数在某个特定的帕累托前沿区域的激增。
另一种替代的距离度量是：
\[dx(\boldsymbol{x},\boldsymbol{y})=\sqrt{\frac{1}{M}\sum_{i=1}^M(x_i-y_i)^2}\]

许多研究都观察到使用适应度共享的多目标优化策略往往要比不使用适应度共享的多目标优化更好。

但是，适应度共享的其中一个问题是在查找前需要确定小生境大小\(σ_{share}\)。Fonseca和Flemin^[3] 提出了一种动态调整\(σ_{share}\)的方法。另一个问题是引入\(σ_{share}\)所增加的计算量。

MOGA是第一个同时使用帕累托排序和小生境的多目标优化算法。

• Step 1: Start with a random initial population \(P_0\). Set \(t = 0\).
  
• Step 2: If the stopping criterion is satisfied, return \(P_t\).
  
• Step 3: Evaluate fitness of the population as follows:
  • Step 3.1: Assign a rank \(r(x,t)\) to each solution \(\boldsymbol{x}∈P_t\) using the ranking scheme: \(r(\boldsymbol{x},t)=1+nq(\boldsymbol{x},t)\).
    
  • Step 3.2: Assign a fitness values to each solution based on the solution’s rank as follows: \[f(\boldsymbol{x},t)=N-\sum_{k=1}^{r(\boldsymbol{x},t)}n_k-0.5(n_{r(\boldsymbol{x},t)}-1)\] 其中\(n_k\)是具有排名\(k\)的个体的数目。
    
  • Step 3.3: Calculate the niche count \(nc(\boldsymbol{x}, t)\) of each solution \(\boldsymbol{x}∈P_t\).
    
  • Step 3.4: Calculate the shared fitness value of each solution \(\boldsymbol{x}∈P_t\) as follows:
    \[f'(\boldsymbol{x},t)=f(\boldsymbol{x},t)/nc(\boldsymbol{x},t)\]
  • Step 3.5: Normalize the fitness values by using the shared fitness values:
    \[f^{''}(\boldsymbol{x},t)=\frac{f^{'}(\boldsymbol{x},t)n_r(\boldsymbol{x},t)}{∑_{\boldsymbol{y}∈P_t,r(\boldsymbol{y},t)=r(\boldsymbol{x},t)}f'(\boldsymbol{x},t)}f(\boldsymbol{x},t)\]
• Step 4: Use a stochastic selection method based on \(f^{''}\) to select parents for the mating pool. Apply crossover and mutation on the mating pool until offspring population \(Q_t\) of size \(N\) is filled. Set \(P_{t+1} = Q_t\).
• Step 5: Set \(t =t +1\), go to Step 2.

SPEA2中使用了一种方法来区分具有相同排名的个体：一个个体周围的密度被定义为与其最近的第\(k\)个个体的距离的相反数。设置\(k\)比设置小生境大小\(σ_{share}\)更为直接。

拥挤距离

拥挤距离(crowding distance)旨在不使用适应度共享方法的参数就可以从最优的帕累托前沿近似中得到均匀的个体分布。NSGA-II中使用了一种拥挤距离的方法：
对于使用帕累托排序生成的若干个非支配前沿\(F_1,...,F_R\)，对于每一个目标函数\(k\)，对\(F_j\)中的每一个解升序排序。设\(l=|F_j|\)，\(\boldsymbol{x}_{[i,k]}\)表示对\(k\)个目标函数排序列表中的第\(i\)个个体。令\(cd_k(\boldsymbol{x}_{[1,k]})=∞\), \(cd_k(\boldsymbol{x}_{[l,k]})=∞\)，对剩下的\(i=2,3,...,l-1\):
\[cd_k(\boldsymbol{x}_{[i,k]})=\frac{z_k(\boldsymbol{x}_{[i+1,k]}-\boldsymbol{x}_{[i-1,k]})}{z_k^{max}-z_k^{min}}\]

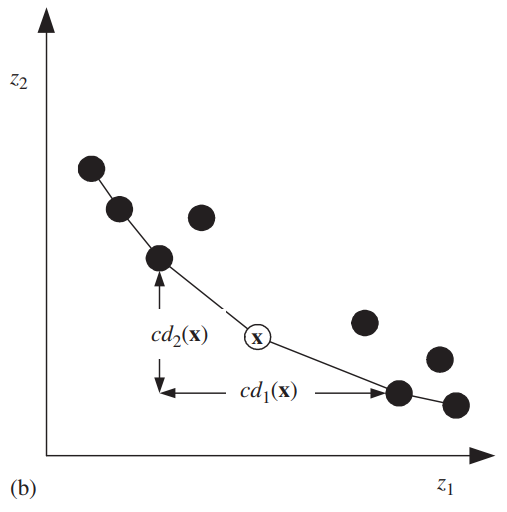
可以发现，\(cd\)越大，相邻个体之间的间距就越大。
最后，对每个\(\boldsymbol{x}\),对所有目标函数的\(cd_k(\boldsymbol{x})\)全部求和:
\[cd(\boldsymbol{x})=∑_kcd_k(\boldsymbol{x})\]

NSGA-II中使用拥挤距离作为稠密度参考来进行选择，称为拥挤锦标赛选择(crowed tournament selection). 在拥挤锦标赛选择中，随机配对的两个个体\(\boldsymbol{x}\),\(\boldsymbol{y}\)。如果两个个体位于同样的非支配前沿，有更高\(cd\)的个体将被选择；如果两个个体在不同的非支配前沿，具有更低排名的个体将被选择。

使用拥挤距离好处是这种衡量个体稠密度的方法不需要使用者提前设置参数\(σ_{share}\)或者是\(k\).

基于网格的稠密度

在基于网格的稠密度(cell-based density)方法中，搜索空间被划分为若干个\(K\)维的超立方网格。每个网格中个体的数量称为该网格的密度，并且定义一个个体的密度就是该个体所在网格的密度。这样的稠密度信息可以辅助实现适应度共享。
比如在PESA中，具有更低稠密度的个体更受欢迎。

• Step 1: Start with a random initial population P0 and set external achieve \(E_0 = ∅, t = 0\).
  
• Step 2: Divide the normalized objective space into \(n^K\) hyper-cubes where \(n\) is the number of grids along a single objective axis and \(K\) is the number of objectives.
  
• Step 3: Update non-dominated archive \(E_t\) by incorporating new solutions from \(P_t\) one by one as follows:
  • Case 1: If a new solution is dominated by at least a solution in \(E_t\), discard the new solution.
  • Case 2: If a new solution dominates some solutions in \(E_t\), remove those dominated solutions from \(E_t\) and add to the new solution to \(E_t\). Update the membership of the hyper-cubes.
    
  • Case 3: If a new solution is not dominated by and does not dominate any solution in \(E_t\), add this solution to \(E_t\). If \(|E_t|=N_E+1\), randomly choose a solution from the most crowded hyper-cubes to be removed. Update the membership of the hyper-cubes.
    
• Step 4: If the stopping criterion is satisfied, stop and return \(E_t\).
• Step 5: Set \(P_t = ∅\), and select solutions from \(E_t\) for crossover and mutation based on the density information of the hyper-cubes. For example, if binary tournament selection is used, the winner is the solution located in the less crowded hyper-cubes. Apply crossover and mutation to generate \(N_P\) offspring and copy them to \(P_{t+1}\).
• Step 6: Set \(t = t + 1\) and go to Step 3.

PESA-II使用了一种更为直接的方式，称为基于区域的选择(region-based selection)。这种选择直接作用于每一个网格而并非选择个体，具有更低稠密度的网格比高密度的网格更有机会被选择。被选择的一个网格中的个体会被随机选择参加交叉和突变。

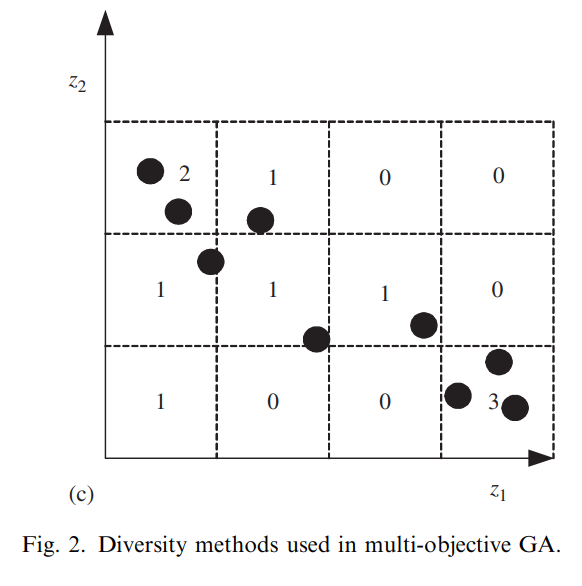
使用基于网格的稠密度的好处有二：其一是这种方法分区域地描述了整个搜索空间中个体的稠密分布。第二，相比于小生境和基于相邻的稠密度方法，基于网格的稠密度计算方法的计算量更低。

精英主义

精英主义(Elitisim)一词在遗传算法中指传统遗传算法中所采用的一种进化策略：迄今为止找到的最优个体总是能够在下一代中存活。在多目标遗传算法中， 迄今为止搜索到的所有的非支配解可以被认为是精英个体。 精英主义在多目标遗传算法中的实现方式有两种：
- 在种群中采用某种机制始终保留精英个体。
- 使用一个外置存储列表保存精英个体，在适当的时候将它们重新引入种群。

种群内保留精英个体

随机选择无法保证精英个体总是能够被选择到中间种群和下一代种群中，因此需要设计一些机制来保证精英个体总是能被选择进入下一代。
一种简单的实现保留精英个体的方式是：假设种群大小始终保持为\(N_P\)，复制当前种群\(P_t\)中所有的精英个体到下一代\(P_{t+1}\)中，然后再对\(P_t\)中的支配解，也就是非精英个体进行选择，直到填满\(P_{t+1}\)。然而，当所有的非支配亲本和子代数量都超过\(N_P\)时，这种方法便不再其作用。有如下几种方式可以解决这个问题：
- Konak和Smith^[4]提出了一种可以动态调整种群大小，并且使用精英策略的多目标遗传算法。在这种算法中，如果种群大小达到上限\(N_{max}\)，\((N_{max}-N_{min})\)个个体会被移出当前种群以保证当前非支配前沿中个体的多样性。
具体的移出策略称为帕累托支配锦标赛选择(Pareto domination tournament selection)：种群中随机配对的两个个体比较相互之间的小生境距离，移出具有较高小生境距离的那个个体（假定现在种群中所有的个体都是非支配个体）。

• NSGA-II使用了固定的种群大小，在第\(t\)代，亲本种群\(P_t\)产生一个具有大小\(N\)的子代种群\(Q_t\). 若干个非支配前沿\(F_1,F_2,...,F_R\)从\(P_t∪Q_t\)中产生。紧接着，按非支配前沿的顺序将各非支配前沿中的个体填充到下一代种群\(P_{t+1}\)，最后一个填入的非支配前沿中的个体按照其拥挤距离\(cd\)从小到大填入下一代种群\(P_{t+1}\)。具体而言可以将上述过程用符号化语言表达为：令\(F_k\)代表的非支配前沿具有如下性质： \(|F_1 ∪ F_2 ∪ ... ∪ F_k|≤N\) 且 \(|F_1 \cap F_2 ∩ ... ∩ F_k|>N\) (\(|·|\)表示集合的大小)。首先，\(F_1,...,F_k\)中所有的个体都被复制到\(P_{k+1}\)中，然后再将\(F_{k+1}\)中最不密集(least-crowded)的\((N-|P_{t+1}|)\)个个体移动到\(P_{k+1}\)中。
  这种方法可以保证当前种群中最优的那一部分——第一非支配前沿\(F_1\)中所有的非支配解都能够在下一代中，如果\(|F_1|≤N\)，那么\(F_1\)中具有更小的拥挤距离的个体将被加入下一代中。

Procedure NSGA-II:
- Step 1: Create a random parent population \(P_0\) of size \(N\). Set \(t =0\).
- Step 2: Apply crossover and mutation to \(P_0\) to create offspring population \(Q_0\) of size \(N\).
- Step 3: If the stopping criterion is satisfied, stop and return to \(P_t\).
- Step 4: Set \(R_t =P_t ∪ Q_t\).
- Step 5: Using the fast non-dominated sorting algorithm, identify the non-dominated fronts \(F_1, F_2, ...,F_k\) in \(R_t\).
- Step 6: For \(i =1,...,k\) do following steps:
- Step 6.1: Calculate crowding distance of the solutions in \(F_i\).
- Step 6.2: Create \(P_{t+1}\) as follows:
- Case 1: If \(| P_{t+1} | + | F_i | ≤ N\), then set \(P_{t+1} =P_{t+1}∪F_i\); - Case 2: If \(| P_{t+1} | + | F_i | >N\), then add the least crowded \(N- | P_{t+1} |\) solutions from \(F_i\) to \(P_{t+1}\).
- Step 7: Use binary tournament selection based on the crowding distance to select parents from \(P_{t+1}\). Apply crossover and mutation to \(P_{t+1}\) to create offspring population \(Q_{t+1}\) of size \(N\). - Step 8: Set \(t =t + 1\), and go to Step 3.

需要注意的是，当\(|R_t| =|P_t ∪ Q_t|>N\)时，NSGA-II的表现是纯粹的精英选择：只有非支配解可以参与选择和交叉。

种群内保留精英个体(maintaining elitist solutions in the population)的好处是这种方法非常容易实现。由于没有外部存储，在这种方法中，种群大小\(N\)是一个重要的超参数。

外置列表保存精英个体

如果使用外置列表\(E\)来保存精英个体，有三个问题是需要考虑的：
- 哪些个体会被存储在\(E\)中？
大多数的多目标遗传算法中，迄今为止找到的所有的非支配解都会存储在外置列表\(E\)中。与此同时，\(E\)这个列表也会进行动态更新，加入新的非支配解；用查找到的更高级的非支配解替代现有\(E\)中受其支配的“非支配解”。
需要注意的是，这样的决策过程需要额外的计算量。
- 外置列表\(E\)的大小
随着搜索过程的进行，找到的非支配解会越来越多，因此最后\(E\)的大小会相当大。有一些修剪(pruning)技术可以控制\(E\)的大小，比如SPEA中使用了一种平均连接聚类来限制\(E\)的大小始终在一个上限\(N^E_{max}\)以内。
具体而言，这种平均连接聚类(average linkage clustering)的过程如下：
1. Initially, assign each solution \(x∈E\) to a cluster \(c_i\), \(C = \{c_1, c_2, ... , c_M\}\).
2. Calculate the distance between all pairs of clusters \(c_i\) and \(c_j\) as follows: \[d(c_i,c_j)=\frac{1}{|c_i||c_j|}∑_{\boldsymbol{x}∈c_i,\boldsymbol{y}∈c_j}d(\boldsymbol{x},\boldsymbol{y})\] 其中\(d(\boldsymbol{x},\boldsymbol{y})\)可以通过之前的\(dz(\boldsymbol{x},\boldsymbol{y})\)或者\(dx(\boldsymbol{x},\boldsymbol{y})\)的计算方法得到。
3. Merge the cluster pair \(c_i\) and \(c_j\) with the minimum distance among all clusters into a new cluster. 4. If \(| C | ≤N\), go to Step 5, else go to Step 2.
5. For each cluster, determine a solution with the minimum average distance to all other solutions in the same cluster (called the centroid solution). Keep the centroid solutions for every cluster and remove other solutions from \(E\).（只保留每个聚类中心的个体）

• 如何引入\(E\)中的个体回到种群？
  在这个问题上有两种策略，其一是可以直接综合\(P_t\)和\(E\)：\(P_t∪E\)，再一同进入选择和遗传操作。
  另一种策略是在\(P_{t+1}\)中为\(E\)保留空间：先将\(E\)的所有个体（大小：\(N_E\)）移动到\(P_{t+1}\)，再从\(P_t\)中选择\(N-N_E\)个个体移动到\(P_{t+1}\).

SPEA和SPEA2两种算法都使用了外置列表来保存精英个体。其他使用外置列表的多目标遗传算法有PESA，RDGA，RWGA，和DMOEA.

Procedure SPEA2:
\(N_E\) : the maximum size of the non-dominated archive \(E\),
\(N_P\) =the population size,
\(k =\sqrt{N_E + N_P}\): parameter for density calculation

• Step 1: Randomly generate an initial solution \(P_0\) and set \(E_0 =∅\).
  
• Step 2: Calculate the fitness of each solution \(\boldsymbol{x}\) in \(P_t ∪ E_t\) as follows:
  • Step 2.1: \(r(\boldsymbol{x}, t) =∑_{\boldsymbol{y}∈(P_t∪E_t),\boldsymbol{y}≻\boldsymbol{x}}s(\boldsymbol{y},t)\) where \(s(\boldsymbol{y},t)\) is the number of solutions in \(P_t ∪ E_t\) dominated by solution \(\boldsymbol{y}\).
    
  • Step 2.2: Calculate the density as: \[m(\boldsymbol{x}, t)=(σ^k_{\boldsymbol{x}} + 1)^{-1}\]
    where \(σ^k_{\boldsymbol{x}}\) is the distance between solution x and its \(k\) th nearest neighbor.
    
  • Step 2.3: Assign a fitness value as: \[f (\boldsymbol{x},t) =r(\boldsymbol{x},t) + m(\boldsymbol{x}, t)\]
• Step 3: Copy all non-dominated solutions in \(P_t ∪ E_t\) to \(E_{t+1}\). Two cases are possible:
  • Case 1: If \(| E_{t+1} | >N_E\), then truncate \((| E_{t+1} | -N_E)\) solutions by iteratively removing solutions with the maximum \(\sigma ^k\) distances. Break any tie by examining \(\sigma ^l\) for \(l=k-1,...,1\) sequentially.
    
  • Case 2: If \(| E_{t+1} | ≤N_E\), copy the best \((N_E- | E_{t+1} |)\) dominated solutions according to their fitness values from \(P_t ∪ E_t\) to \(E_{t+1}\).
    
• Step 4: If the stopping criterion is satisfied, stop and return non-dominated solutions in \(E_{t+1}\).
  
• Step 5: Select parents from Etþ1 using binary tournament selection with replacement.
  
• Step 6: Apply crossover and mutation operators to the parents to create NP offspring solutions. Copy offspring to \(P_{t+1}\), \(t = t + 1\), and go to Step 2.

条件限制

大多数真实的多目标优化问题中，优化目标常常有各种各样的限制(constraint)。在单目标遗传算法中，用来进行条件限制的策略有四种：
- I. 舍弃不可能实现的解决方案（又称为“Death Penalty”）
- II. 使用惩罚函数降低不可能实现个体的适应度
- III. 设计遗传操作使得种群总是可以产生可行的个体 - IV. 设计某种机制使得不可能个体变成可行的个体（又称为“repair”）

目前，对多目标遗传算法中条件限制问题的研究并不充分，大多数的多目标遗传算法并不考虑条件限制。不过，策略I, III,IV可以直接应用于多目标遗传算法。
Jimenez等人^[5]提出了一种基于小生境的选择策略来实现条件限制，过程如下：
- Step 1: Randomly chose two solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) from the population.
- Step 2: If one of the solutions is feasible and the other one is infeasible, the winner is the feasible solution, and stop. Otherwise, if both solutions are infeasible go to Step 3, else go to Step 4.
- Step 3: In this case, solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are both infeasible.
Then, select a random reference set \(C\) among infeasible solutions in the population. Compare solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) to the solutions in reference set \(C\) with respect to their degree of infeasibility. In order to achieve this, calculate a measure of infeasibility (e.g., the number of constraints violated or total constraint violation) for solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\), and those in set \(C\). If one of solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) is better and the other one is worse than the best solution in \(C\), with respect to the calculated infeasibility measure, then the winner is the least infeasible solution.
However, if there is a tie, that is, both solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are either better or worse than the best solution in \(C\), then their niche count in decision variable space is used for selection. In this case, the solution with the lower niche count is the winner.
- Step 4: In the case that solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are both feasible, select a random reference set \(C\) among feasible solutions in the population. Compare solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\) to the solutions in set \(C\). If one of them is non-dominated in set \(C\), and the other is dominated by at least one solution, the winner is the former. Otherwise, there is a tie between solutions \(\boldsymbol{x}\) and \(\boldsymbol{y}\), and the niche count of the solutions is calculated in decision variable space. The solution with the smaller niche count is the winner of the tournament selection.

简单来说，该方法使用了一个参考集合\(C\)，该参考集合中的所有个体都是可行的。然后随机配对种群中的两个个体\(\boldsymbol{x}\) 和 \(\boldsymbol{y}\) 以 \(C\)为参照对比可行性，可行性更高的个体胜出。如果这两个个体本身都是可行的，则比较两者的小生境距离，小生境距离更小的个体胜出。

上述的这种方法是一种较为综合的处理限制条件的方法，在处理过程中还可以有效地保证个体多样性。这种方法的缺点是计算复杂度以及引入了例如小生境距离和参考种群\(C\)相关的超参数。

不过上述方法仍然许多可以改进的地方，比如第三步中\(\boldsymbol{x}\) 和 \(\boldsymbol{y}\)的可行性可以直接比较而不需要实用一个参考集合\(C\);再比如第四步中小生境距离可以在目标函数的空间中直接得出，不需要回到变量的空间(decision variable space)中再进行计算。

Deb等人提出的NSGA-II中^[6]提出了有限制的锦标赛选择机制(constrained tournament selection)。在这种机制中，如果个体\(\boldsymbol{x}\)满足如下任何一个条件，称个体\(\boldsymbol{x}\)有条件地支配(constrain-dominate)个体\(\boldsymbol{y}\)：
- \(\boldsymbol{x}\)可行，\(\boldsymbol{y}\)不可行 - \(\boldsymbol{x}\)和\(\boldsymbol{y}\)都不可行，但是\(\boldsymbol{x}\)对条件的破坏低于\(\boldsymbol{y}\) - \(\boldsymbol{x}\)和\(\boldsymbol{y}\)都可行，\(\boldsymbol{x}\)支配\(\boldsymbol{y}\)

首先，若干个条件限制的非支配前沿\(F_1,...,F_R\)可以通过使用上述的“有条件支配”的定义进行帕累托排序得出。在这样的选择机制中，随机选择两个个体\(\boldsymbol{x}\) 和 \(\boldsymbol{y}\)，然后比较两者在条件限制的非支配前沿中的地位。
这种方式的优点是只需要引入非常少的超参数，而且对原本多目标遗传算法的改动也比较小。

并行多目标

并行化单目标遗传算法的一种方法是通过局部搜索进行的，这种算法通常被称为Memetic算法，使用Memetic算法的并行化步骤如下：
- Step 1: Start with an initial solution \(\boldsymbol{x}\).
- Step 2: Generate a set of neighbor solutions around solution \(\boldsymbol{x}\) using a simple perturbation rule. - Step 3: If the best solution in the neighborhood set is better than \(\boldsymbol{x}\), replace \(\boldsymbol{x}\) with this solution and go to Step 2, else stop.

局部搜索的算法总是在初始个体附近是凸函数(convex)时具有很好的搜索性能。然而这种条件对于使用标准遗传算子的进化算法是很难达到的。并行化多目标遗传算法需要解决的问题有：
- 如何选择一个解以在其周围开始局部搜索
- 当多个局部非支配的解(none-dominated local solution)存在时，如何定义一个解周围的解比这个解更好

有非常多的方法旨在解决上述问题：
- Ishibuchi和Murata ^[7] 提出了一种基于交叉的局部搜索方式，这种方式使用与子代的亲本相同的权重向量来衡量领域的个体。相似地，Ishibuchi等人^[8]在局部搜索中同样使用了有权的目标函数线性组合来衡量个体，但是局部搜索只能选择性地用于有希望的解决方案，并使用随机生成的权重而不与子代的亲本相同。

• Konwles和Conrne ^[9] 提出了一种基于Memetic算法的PAES算法改进，称为M-PAES。在M-PAES中，基于之前个体的相邻区域搜索到的个体只会与局部非支配解集合比较表现，然后决定是否更新这个解集。
  这种方法中局部搜索的终止条件有二：搜索的个体数达到上限或者搜索路线经历了最大数量的局部移动但是没有任何改进。

• Tan等人 ^[10] 提出一种基于相邻个体的搜索方法。这种方法中，局部搜索的邻域大小取决于解决方案的稠密度或拥挤程度。由于在应用局部搜索时具有选择性，这种策略在保持多样性的同时也具有计算效率。

总结：不同的多目标遗传算法以及评述

Algorithm	Fitness Assignment	Diversity Mechanism	Elitism	External Population	Advantages	Disadvantages
VEGA	Each subpopulation is evaluated with respect to a different objective	No	No	No	First MOGA Straightforward implementation	Tend converge to the extreme of each objective
MOGA	Pareto ranking Fitness sharing by niching	No	No	Simple extension of single objective GA	Usually slow convergence	Problems related to niche size parameter
WBGA	Weighted average of normalized objectives	Niching	No	No	Simple extension of single objective GA	Difficulties in nonconvex
NPGA	No fitness assignment, tournament selection	Niche count as tie breaker in tournament selection	No	No	Very simple selection process with tournament selection	- Problems related to niche size parameter - Extra parameter for tournament selection
RWGA	Weighted average of normalized objectives	Randomly assigned weights	Yes	Yes	Efficient and easy implement	Difficulties in nonconvex objective function space
PESA	No fitness assignment	Cell-based density	Pure elitist	Yes	- Easy to implement Performance depends on - Computationally efficient cell size s	Prior information needed about objective space
PAES	Pareto dominance is used to replace a parent if offspring dominates	Cell-based density as tie breaker between offspring and parent	Yes	Yes	- Random mutation hill climbing strategy - Easy to implement Performance depends on	- Not a population based approach - Computationally efficient cell sizes
NSGA	Ranking based on non-domination sorting	Fitness sharing by niching	No	No	Fast convergence	Problems related to niche size parameter
NSGA-II	Ranking based on non-domination sorting	Crowding distance	Yes	No	- Single parameter (\(N\)) - Well tested - Efficient	Crowding distance works in objective space only
SPEA	Ranking based on the external archive of non-dominated solutions	Clustering to truncateexternal population	Yes	Yes	- Well tested - No parameter for clustering	Complex clustering algorithm
SPEA-2	Strength of dominators	Density based on the k-th nearest neighbor	Yes	Yes	- Improved SPEA - Make sure extreme points are preserved	Computationally expensive fitness and density calculation
RDGA	The problem reduced to bi-objective problem with solution rank and density as objectives	Forbidden region cell based density	Yes	Yes	- Dynamic cell update - Robust with respect to the number of objectives	More difficult to implement than others
DMOEA	Cell-based ranking	Adaptive cell-based density	Yes (implicitly)	No	- Includes efficient techniques to update cell densities - Adaptive approaches to set GA parameter	More difficult to implement than others

1. C. A. C. Coello, "Evolutionary multi-objective optimization: a historical view of the field," IEEE Computational Intelligence Magazine, vol. 1, no. 1, pp. 28-36, 2006, doi: https://doi.org/10.1109/MCI.2006.1597059. ↩︎
2. Goldberg DE. Genetic algorithms in search, optimization, and machine learning. Reading, MA: Addison-Wesley; 1989. ↩︎
3. Fonseca CM, Fleming PJ. Multiobjective genetic algorithms. In: IEEE colloquium on ‘Genetic Algorithms for Control Systems Engineering’ (Digest No. 1993/130), 28 May 1993. London, UK: IEE; 1993. ↩︎
4. Konak A, Smith AE. Multiobjective optimization of survivable networks considering reliability. In: Proceedings of the 10th international conference on telecommunication systems. Monterey, CA: Naval Postgraduate School; 2002. ↩︎
5. Jimenez F, Gomez-Skarmeta AF, Sanchez G, Deb K. An evolutionary algorithm for constrained multi-objective optimization. In: Proceedings of the 2002 world congress on computational intelligence—WCCI’02, 12–17 May, 2002. Honolulu, HI, USA: IEEE; 2002. ↩︎
6. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 2002;6(2):182–97. ↩︎
7. Ishibuchi H, Murata T. Multi-objective genetic local search algorithm. In: Proceedings of the IEEE international conference on evolutionary computation, 20–22 May, 1996. Nagoya, Japan: IEEE;1996. ↩︎
8. Ishibuchi H, Yoshida T, Murata T. Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling. IEEE Trans Evol Comput 2003;7(2): 204–23. ↩︎
9. Knowles JD, Corne DW. M-PAES: a memetic algorithm for multiobjective optimization. In: Proceedings of the 2000 congress on evolutionary computation, 16–19 July, 2000. La Jolla, CA, USA: IEEE; 2000. ↩︎
10. Tan KC, Lee TH, Khor EF. Evolutionary algorithms with dynamic population size and local exploration for multiobjective optimization. IEEE Trans Evol Comput 2001;5(6):565–88. ↩︎