多目标遗传算法：NSGA和NSGA-II

N. Srinivas and K. Deb, "Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms," in Evolutionary Computation, vol. 2, no. 3, pp. 221-248, Sept. 1994, doi: 10.1162/evco.1994.2.3.221.
K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, "A fast and elitist multiobjective genetic algorithm: NSGA-II," in IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182-197, April 2002, doi: 10.1109/4235.996017.

多目标优化理论概述

在数学上，多目标优化问题可以被公式化为如下表述：
如果多目标问题的每一种解都可以使用\(n\)维空间\(X\)中的一个的向量进行表示：\(\boldsymbol{x}=\{x_1,x_2,...,x_n\}\)，那么多目标优化就是找到一个解\(\boldsymbol{x^*}\)使得\(K\)个目标函数(objective function)\(z_i(\boldsymbol{x})\)具有最小值:
\[z(x^*)=\{z_1(\boldsymbol{x^*}),z_2(\boldsymbol{x^*}),...,z_n(\boldsymbol{x^*})\}\]

同时，搜索空间\(X\)受到一系列的约束条件(constrain)\(g\)的限制：\(g_j(\boldsymbol{x^*})=b_j\)，\(j=1,...,m\).

实际情况是，许多约束的满足条件彼此之间会冲突，因此实际上想要找到一个多目标解使得所有目标函数同时达到最优解几乎是不可能的。因此，事实上多目标优化是寻找一组最优化的近似解，这个解在每一个目标函数中的结果都在可以接受的范围内，而且没有其他的解可以比这个解至少在一个目标函数中更好。
详细的帕累托优化理论和定义请参考：多目标遗传算法综述.

非支配的数学表示可以是：对于一系列多目标适应度函数\(\boldsymbol{f}=(f_1,f_2,...,f_k)\)和两个多目标个体\(x_i,x_j\)，都有：
\[\boldsymbol{f}(x_i)=(f_1(x_i),f_2(x_i),...,f_k(x_i))\] 令\(f_m(x_j)∈\boldsymbol{f}(x_j)\),\(f_m(x_i)∈\boldsymbol{f}(x_i)\)，如果： \[f_m(x_j)>f_m(x_i)\] 且， \[∀f_n(x_j)≥f_n(x_i),m ≠ n\] 那么\(x_j≻x_i\).

传统方法

标量化

最常见的多目标优化的难点是目标之间的冲突：无法同时找到所有目标的最优。因此在数学上的帕累托最优是提供具有最小冲突的解决方案。在搜索空间中，这些解决方案表现为空间中的点，这些点从单个目标上看是最优的。但是这样的方法无法满足决策者调整不同目标满足最优的优先程度。因此，传统的一种解决多目标最优化的方法是将向量通过使用加权平均转化为单目标优化，这个过程中个体向量被标量化(scalarize)。通过权重向量来反映和调整每个目标的优先级。

目标函数加权

所有的目标函数使用一个使用一个权重向量\(\boldsymbol{w}\)进行线性组合：
\[Z=∑_{i=1}^Nw_if_i(\boldsymbol{x})\] 如此，对于目标函数的优先程度反映在权重向量\(\boldsymbol{w}∈(0,1)\)中。通常，个体在每个目标上的值先被计算出来，然后根据决策者设置的优先级使用如上的公式将多目标优化问题转化为单目标优化问题。
这种算法非常简单，易于实现，而且可以根据优先级控制目标函数。但是存在两个问题：第一，最优化的结果极大地依赖于权重向量。其二，决策者可能还想知道其他的备选方案。

距离函数

这种方法使用需求层级向量(demand-level vector)\(\overline{\boldsymbol{y}}\)来对多目标优化问题进行标量化：
\[Z=\left[\sum_{i=1}^N|f_i(\boldsymbol{x})-\overline{y}_i|^r\right]^{1/r},1≤r<∞\] 其中需求层级向量\(\overline{\boldsymbol{y}}\)的值是由决策者预先设置好的。通常使用欧氏距离\(r=2\)。
这种方法的优化结果极大地依赖于对需求层级向量的设置。错误的需求层级向量的设置会导致错误的帕累托优化结果，对需求层级向量需要决策者有足够的先验知识。
这种方法其实与目标函数加权非常类似，只是在这种方法中提供的权重表示对目标的满足程度，而前者的权重强调目标函数的重视程度。

最小-最大博弈

另一种解决目标冲突的方法是使用最小-最大博弈(Min-Max)：在最大化每个目标函数的前提下最小化目标函数之间的冲突：
\[min[𝑭(\boldsymbol{x})]=max[Z_j(\boldsymbol{x})],j=1,2,...,N\] 其中：
\[Z_j(\boldsymbol{x})=\frac{f_j-\overline{f}_j}{\overline{f}_j}\] \(\overline{f}_j\)是在目标函数\(j\)上的平均适应度。
对于相同优先级的目标函数，这种方法可以得出相对折中的最优方案；同时可以通过引入标量权重来设置目标函数的优先级。

如上传统方法的缺点在于，虽然这些方法可以保证帕累托优化，但是每次只能找到一个点而不能够一次性找到多个帕累托最优解。在充满噪声和离散变量的空间中，这些方法工作效率低下。同时其中的一些方法对于先验知识的要求很高，并且对权重和需求的设置十分敏感。

VEGA和种群多样性的改进

Schaffer提出的VEGA是最早的多目标优化遗传算法。VEGA根据目标函数的个数将整个种群分成了若干个子种群，其中每个子种群对应一个特定的目标函数进行优化：每一代中按照该目标函数赋予适应度、进行选择后再综合进行交叉和变异等遗传操作。
VEGA最大的问题是无法保证其无偏性：在进化数代之后，VEGA的进化方向总是倾向于帕累托前沿的某些特定区域和某些特定的个体。解决VEGA中种群多样性问题的办法有三种： - 其一，使用一种叫做非支配选择(nondominated selection)的选择方法，这种选择方法引入了惩罚函数(peanalty function)：惩罚函数使用一个非常小的固定值减少受支配个体的复制次数。这种方法的缺点是，在种群中只有少数非支配解时，这些非支配解的适应度会非常高，造成严重的选择压力。
- 另一种选择机制称为配对选择(mating selection)，在这种机制下，一个随机选择的个体和与其具有最大欧氏距离的个体进行配对，旨在通过配对增加种群的多样性。但是由于第一个个体是随机选择的，其无法保证比它更差的个体与其配对并参与到之后的遗传操作中。有些文献甚至认为，配对选择的性能还不如随机配对。
- Goldberg提出了一种称为适应度共享(fitness sharing)的方法为NSGA所采用的方法，这种方法相比于前两者都更好，将在之后详细描述。

NSGA

非支配排序

帕累托排序(Pareto ranking)或者称为非支配排序(nondominated ranking)利用了帕累托最优理论中“支配”的概念来为不同的个体赋予适应度。简单来说，种群中的个体适应度表示为排序。具有更高支配地位的个体会具有更好的适应度。在本文中，越好的个体具有更低的适应度，排名更小更靠前。
Goldberg提出了第一种帕累托排序方法，简单来说就是对于当前种群中的所有个体，选择出其中的帕累托解并移入另一个列表中，然后再筛选剩余个体中的新的帕累托解。（即去掉上一次的帕累托解后现有集合中新的不受其他种群支配的个体），如此往复。
其过程详细描述如下：
- 首先从整个种群中找到所有的非支配个体，这些非支配个体对应的多目标函数的值构成第一非支配前沿。
- 然后所有在第一非支配前沿的个体都被赋予一个非常大的冗余适应度(dummy fitness)，使得第一个非支配前沿中最差个体的适应度仍然高于第二个非支配前沿中最好个体的适应度。
- 接着，为了保持种群的多样性，具有相同冗余适应度的个体会通过适应度共享被惩罚。适应度共享机制会在后文中详细介绍。
- 然后第一非支配前沿的所有个体被给予适应度后从种群中移除，然后再看种群中剩余所有个体中新产生的非支配个体，这些个体构成第二非支配前沿。如此重复，直到所有的个体都被绑定到一个非支配前沿中。

非支配排序的计算量

对于\(M\)个目标函数，大小为\(N\)的种群，种群中的每一个个体都需要与其他个体在所有目标函数的维度上进行比较才能确定其受支配的程度。这样的比较需要的计算复杂度为\(O(MN)\)。要想找到第一非支配前沿中所有的个体，计算复杂度为\(O((MN)×N)=O(MN^2)\).
在最坏的情况下，寻找到第二个非支配前沿中所有个体的计算复杂度也为\(O(MN^2)\)。如此寻找到第\(N\)个非支配前沿所需要的计算复杂度应当为\(O((MN^2)×N)=O(MN^3)\).
同时储存每个个体的排名还需要\(O(N)\)的计算量。

适应度共享

在NSGA中，同一个非支配前沿的个体进行适应度共享。适应度共享的过程是将个体原来的适应度除以其附近个体的个数。
NSGA中对于“附近”的定义属于称为小生境(niching)，\(σ_{share}\)是小生境大小，代表的是两个个体被认定在同一个小生境的最大距离。

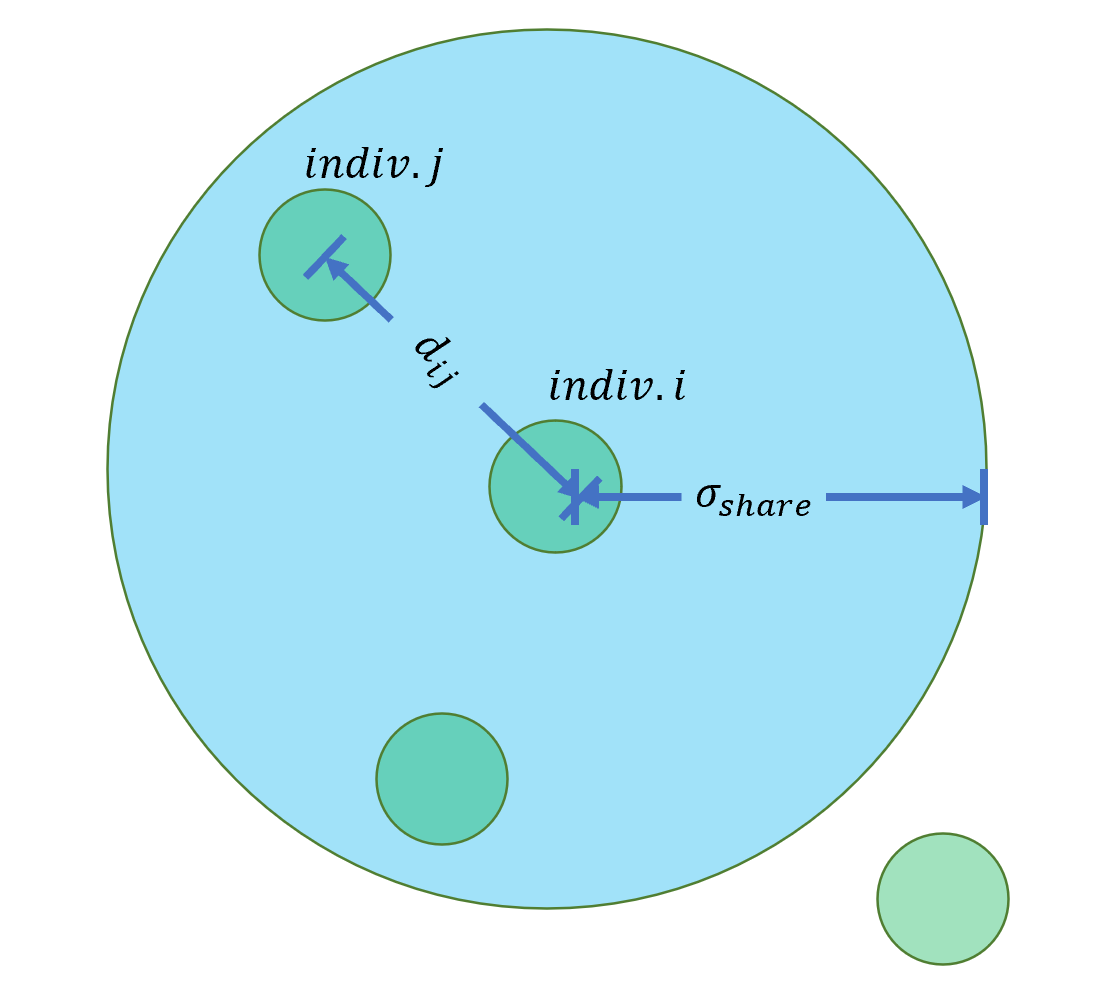
具体用公式表示为：

\[f'_i=\frac{f_i}{nc_i}\] \[nc_i=∑_kSb(d_{ij})\] \[Sb(d_{ij})=\begin{cases} 1-\left(\frac{d_{ij}}{σ_{share}}\right)^2,\text{if }d_{ij}<σ_{share};\\ 0, \text{otherwise}. \end{cases}\] 其中，\(d_{ij}\)是当前非支配前沿中同一个小生境中个体\(i\)和个体\(j\)之间的距离。而每个个体附近个体的数量定义为小生境距离\(nc_i\)，它是在所有目标函数方向上的\(Sb(d_{ij})\)的和。

NSGA的算法流程图如下：

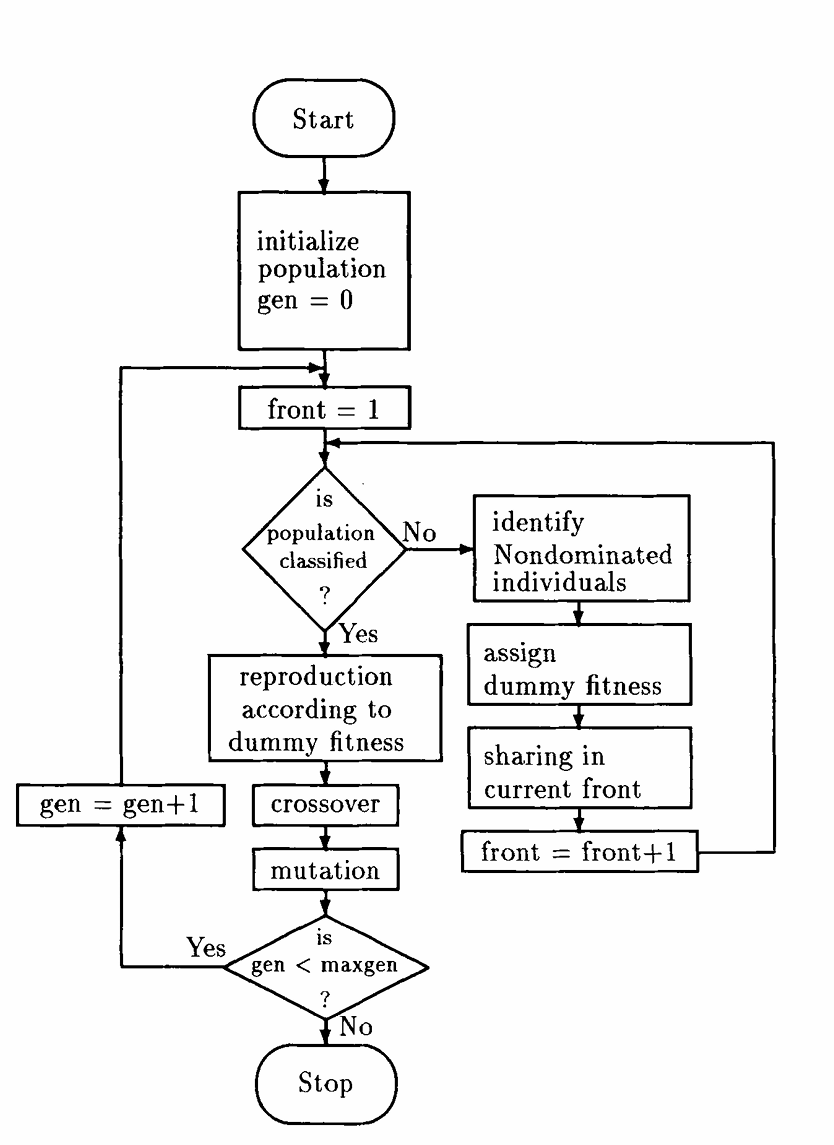
在非支配排序后，NSGA的原论文中采用了随机余数选择以及常规的交叉和突变算子。由于第一非支配前沿中的个体具有最大的适应度，在随机余数选择中它们往往可以得到相当多的复制次数。这样的机制可以保证快速收敛。适应度共享机制可以保证搜索始终朝着更多未搜索的帕累托前沿的区域进行。

近似方法比较

MOGA

Fonesca 和 Fleming提出的MOGA同样也使用了Goldenberg的非支配排序的思想。对于一个个体，首先想找到在种群中严格支配该个体的个体数量，然后该个体的排名是这些支配个体的排名+1。因此可能存在具有相同排名的个体。然后选择过程会依据这个排名删除一些个体，进而形成中间种群进行交配。
MOGA虽然也使用了非支配排序，但是相比于NSGA具有如下的缺点：
- 在选择阶段直接去掉一些个体可能会导致提前收敛。
- MOGA也使用了小生境作为适应度共享的方法，但是其距离度量基于的是每个个体在目标函数上的值而非个体本身的参数，这样的方法虽然可以保证在目标函数空间中的多样性，但是无法保证在个体本身分布的参数空间中的种群多样性。
- 实验证明，MOGA可能无法在同一个目标函数值的位置上找到多个帕累托解。

帕累托支配锦标赛

在多目标优化问题中，Nafpliotis和Goldberg使用了帕累托支配锦标赛(Pareto domination tournaments)而非非支配排序。
在帕累托支配锦标赛中，首先从现在的种群内中随机挑选\(t_{dom}\)个个体形成一个参考集合(称为comparision set)作为比较的依据。然后两个个体被随机地从种群中挑选出来并与参考集合中的个体进行比较，然后根据受支配情况决定两个个体中哪一个个体是胜者：
如果两个个体其中一个个体受参考集合个体支配，另一个支配参考集合的个体，那么支配个体为胜者；当两个个体都为非支配个体或者支配个体时，则根据个体的小生境大小进行比较，小生境大小更大的个体胜出。
在NSGA中并没有采用这种锦标赛方法，原因如下：
- 帕累托支配锦标赛的结果依赖于对参考集合大小\(t_{dom}\)的设置：如果\(t_{dom}\)过小，那么将无法筛选出真正的非支配解；如果\(t_{dom}\)过大，种群中过多数量的个体被筛选，进而导致过早收敛。
- 其次，帕累托支配锦标赛的结果也依赖于小生境大小\(nc\)以及对距离的定义。

相比帕累托支配锦标赛，NSGA中的非支配排序对Goldenberg的非支配排序的思想实现更好。

NSGA的缺点

在NSGA-II的论文中提到NSGA的缺点主要有如下三点：
- 计算复杂度高：NSGA的计算复杂度为\(O(MN^3)\)（其中\(M\)是目标点的数量，\(N\)是种群大小）。这个计算复杂度主要是由于每一代中都要执行非支配排序所造成的。庞大的计算复杂度导致NSGA在种群大小非常大时消耗大量的计算资源。
- 精英策略(elitism)可以提高遗传算法的性能、同时保护优秀的个体。NSGA论文提出的时代精英策略还不受到重视，因此NSGA没有使用精英策略。
- NSGA中引入了小生境距离\(σ_{share}\)这个超参数。导致NSGA的结果也依赖于对小生境距离\(σ_{share}\)的设置。

NSGA-II

快速非支配排序

在进行快速非支配排序前，对每个个体计算如下的两个属性：
- 支配大小(dominiation count)\(n_p\)：表示支配个体\(p\)的支配者数量。
- \(S_p\):由\(p\)支配的个体所组成的集合。这一步计算需要\(O(MN^2)\)次比较。

然后对所有在第一非支配前沿的个体，令他们的支配大小为0：\(n_p=0\)。然后找到这些个体的\(S_p\)，并且对在\(S_p\)中的个体的\(n_p\)减1。 这个过程中如果发现某个个体的\(n_p=0\)，那么该个体属于第二非支配前沿。
然后对第二非支配前沿的所有个体重复上述操作，如此循环直到所有的个体都被找到对应的非支配前沿。

整个算法描述如下：
\[\begin{aligned} \text{for each } p∈P\\ S_p=∅&\\ n_p=0&\\ \text{for each } q ∈ &P\\ \text{if } p≻&q \text{ then}\\ S_p&=S_p∪\{q\}\\ \text{else if }&q≻p \text{ then}\\ n_p&=n_p+1\\ \\ \text{if }n_p=0, &\text{then}\\ p_{rank}&=1\\ 𝑭_1&=𝑭_1∪\{p\}\\ \\ \end{aligned}\] \[\begin{aligned} i=1&\\ \text{while }&𝑭_i≠∅:\\ Q=&\emptyset \\ &\text{for each } p \in 𝑭_i:\\ &\text{  for each } q \in S_p:\\ &\text{           }n_q=n_q-1\\ &\text{           }\text{if }n_q=0\text{ then}\\ &\text{                      }q_{rank}=i+1\\ &\text{                      }Q=Q∪\{q\}\\ i=i&+1 \end{aligned}\]

快速非支配排序的计算量

如果一个个体已经被放入到了对应的非支配前沿，那么该个体在排序过程中将不再被访问。
对于位于第二及以上的非支配前沿中的个体，其\(n_p\)最大为\(N-1\)，因此在这种情况下每个个体\(p\)在其\(n_p\)减少到0之前最多被访问\(N-1\)次。最坏的情况下，这样的个体\(p\)有\(N-1\)个，因此每个目标的计算复杂度为\(O(N^2)\).
从另一个角度思考该计算过程：对于如上算法的第一个大循环（\(\text{for each } p∈𝑭_i\)），其最多运行\(N\)次，其中的内循环(\(\text{  for each } q \in S_p\))最多运行\(N-1\)次，因此每个目标的计算复杂度为\(O(N^2)\).
一共有\(M\)个目标，也就是说个体会在每个目标上都进行比较，因此整个算法总体的计算复杂度为\(O(MN^2)\).
每个个体需要保存对应的\(n_p\)和\(S_p\)，存储上需要\(O(N^2)\)的计算量。

从如上的分析可以看出，快速非支配排序简化了非支配排序中的比较过程。所有的非支配前沿只需要一次遍历就可以被确定。

拥挤距离

NSGA-II延续了NSGA中的适应度共享的思路。但是NSGA-II的作者认为，NSGA中基于小生境的适应度共享存在如下问题：
- 基于小生境的适应度共享受到超参数小生境距离\(σ_{share}\)的影响。
- 由于每个个体都需要与其他个体进行比较，因此NSGA中的适应度共享的计算复杂度为\(O(N^2)\).

为了解决上述问题，NSGA-II中提出了一种基于拥挤距离(crowding distance)的适应度共享方案。这种算法不依赖任何超参数的设置，并且拥有更小的计算量。

稠密度估计

为了找到相邻的个体，在进行稠密度估计之前需要根据个体在各个目标函数的值对整个种群进行排序。然后以个体\(i\)附近相邻两个个体\(i-1\)和\(i+1\)在各个目标函数方向上的距离的平均值来估计每个个体周围的个体分布的稠密程度。

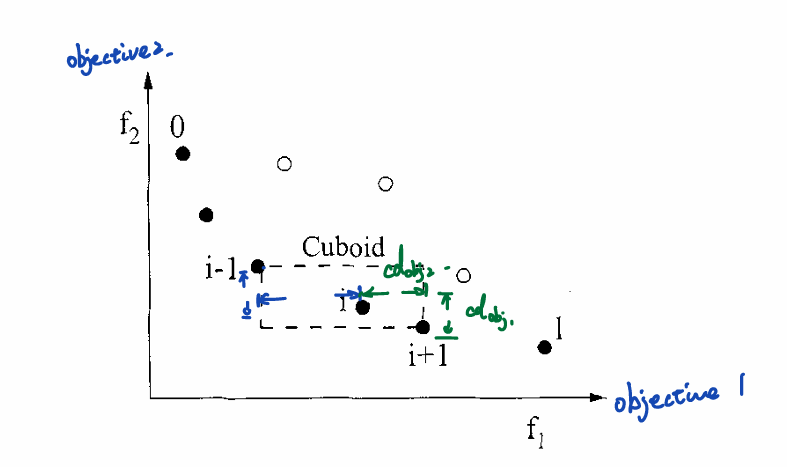
考虑到首尾个体（拥有最大和最小目标函数值的个体）在一边不存在相邻个体，定义它们的拥挤都为无穷。其余个体的拥挤距离\(cd\)为附近相邻两个个体\(i-1\)和\(i+1\)在各个目标函数方向上的距离的平均值的极差归一化结果。
对于使用帕累托排序生成的若干个非支配前沿\(F_1,...,F_R\)，对于每一个目标函数\(k\)，对\(F_j\)中的每一个解升序排序。设\(N=|F_j|\)，\(\boldsymbol{x}_{[i,k]}\)表示对\(k\)个目标函数排序列表中的第\(i\)个个体。令\(cd_k(\boldsymbol{x}_{[1,k]})=∞\), \(cd_k(\boldsymbol{x}_{[l,k]})=∞\)，对剩下的\(i=2,3,...,N-1\):
\[cd_k(\boldsymbol{x}_{[i,k]})=\frac{z_k(\boldsymbol{x}_{[i+1,k]}-\boldsymbol{x}_{[i-1,k]})}{z_k^{max}-z_k^{min}}\] 个体的拥挤距离表示为：
\[i_{distance}=cd(\boldsymbol{x_i})=∑_kcd_k(\boldsymbol{x}_{[i,k]})\] 这个算法总的计算复杂度为\(O(MNlogN)\)。
可以看出拥挤距离\(cd\)反应了个体\(i\)周围的个体分布稠密程度，\(cd\)越小，说明\(i\)的周围越拥挤。

基于拥挤的选择

经过快速非支配排序和适应度共享的个体\(i\)现在拥有如下的两个属性：
- 非支配排名(nondomination rank)：\(i_{rank}\) - 拥挤距离(crowding distance)：\(i_{distance}\)

定义基于拥挤距离的选择算子\(≻_n\)：
如果\(i_{rank}\<j_{rank}\)（排名越靠前越优）或者 \([(i_{rank}=j_{rank})AND(i_{distance}>j_{distance})]\) ，称\(i≻_nj\)。
也就是说，两个个体先比较非支配排名，非支配排名靠前的个体胜出；如果两者的排名相同，那么比较两者的拥挤距离，拥挤距离大的胜出。

主循环

主循环中应用了精英机制。具体的表述如下：
定义种群\(P\)经过锦标赛、重组和突变后产生了后代\(Q\)，它们的种群大小都固定为\(N\)，然后进行如下的操作：
- 创建一个列表\(R_t=P_t∪Q_t\)，其列表大小为\(2N\)
- 对\(R_t\)使用快速非支配排序 - 将\(F_1\)到\(F_N\)中的个体按照基于拥挤距离的选择算子填充一个大小为\(N\)的列表\(P'\)，即，\(F_1\)中的个体优先填入\(P'\)，然后依次填入\(F_2,F_3,...\)的个体。直到\(P'\)的种群大小为\(N\)。需要注意的是，最后一个填入\(P'\)的非支配前沿中的个体按照基于拥挤的选择填入个体。

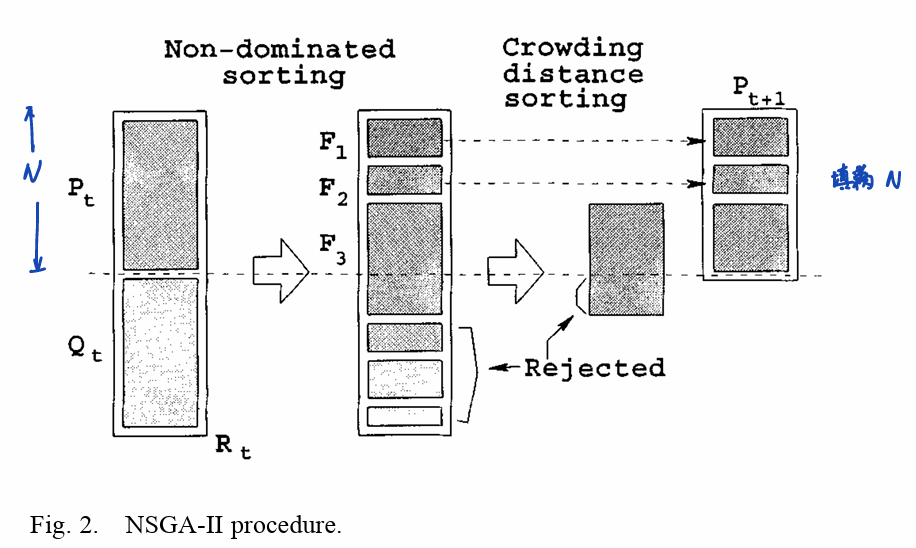
最坏的情况下，一轮主循环需要的计算量如下：
- 快速非支配排序：\(O(M(2N)^2)\)
- 适应度共享：\(O(M(2N)log(2N))\)
- 基于拥挤的选择:\(O(2Nlog(2N))\)
整个算法的计算复杂度为\(O(MN^2)\)，取决于非支配排序。

条件限制

在单目标优化中，常见的条件限制方法是使用锦标赛算法：随机配对两个个体，两个个体中具有更高实现度的个体将被选中。由于单目标优化中不需要在各个目标函数的维度上都进行比较，因此单目标优化中没必要使用惩罚函数。
借用这种方法，NSGA-II中提出了有限制的锦标赛选择机制(constrained tournament selection)。在这种机制中，如果个体\(\boldsymbol{x}\)满足如下任何一个条件，称个体\(\boldsymbol{x}\)有条件地支配(constrain-dominate)个体\(\boldsymbol{y}\)：
- \(\boldsymbol{x}\)可行，\(\boldsymbol{y}\)不可行 - \(\boldsymbol{x}\)和\(\boldsymbol{y}\)都不可行，但是\(\boldsymbol{x}\)对条件的破坏低于\(\boldsymbol{y}\) - \(\boldsymbol{x}\)和\(\boldsymbol{y}\)都可行，\(\boldsymbol{x}\)支配\(\boldsymbol{y}\)

首先，若干个条件限制的非支配前沿\(F_1,...,F_R\)可以通过使用上述的“有条件支配”的定义进行帕累托排序得出。在这样的选择机制中，随机选择两个个体\(\boldsymbol{x}\) 和 \(\boldsymbol{y}\)，然后比较两者在条件限制的非支配前沿中的地位。
使用有条件的支配这一概念时，可行个体的排名将比不可行个体的排名更优。同时这样简单的定义改变不会影响NSGA-II中快速非支配排序的计算复杂度。