电力线缆的寿命预测模型

电力线缆的寿命预测模型可以分为如下几类：阿伦尼乌斯模型(Arrhenius model)、逆幂律模型(Inverse Power Low)、指数衰减模型(exponential decay model) ^{<span class="hint--top hint--rounded" aria-label="Chinh Dang, J. . -L. Parpal and J. . -P. Crine, "Electrical aging of extruded dielectric cables: review of existing theories and data," in IEEE Transactions on Dielectrics and Electrical Insulation, vol. 3, no. 2, pp. 237-247, April 1996, doi: 10.1109/94.486776.">[1]}。

阿伦尼乌斯模型

阿伦尼乌斯模型(Arrhenius model)是使用温度应力试验时最典型、应用最广的加速模型，来源是阿伦尼乌斯在1889年所创立的化学反应速率常数随温度变化关系的经验公式。它表示了实体的某个性质\(M\)（称为退化量）的退化速率随着开氏温度\(T\)的变化关系：
\[\frac{∂M}{∂t}=A\exp(-\frac{E_a}{k_bT})\] 其中\(A\)是常数;\(E_a\)是失效所需要的活化能(activation energe)，单位为\(eV\);\(k_b=8.617×10^{-5}eV/K\)是玻尔兹曼常数。
如果实体初始退化量为\(M_1\)，经过\(\Delta t\)后退化量为\(M_2\)，有：
\[Δt=\frac{M_2-M_1}{A\exp(-\frac{E_a}{k_bT})}\] 当\(M_2=M_p\)即退化量达到认定为失效的阈值时，此时\(Δt=L\)为实体的剩余寿命，对上述式子两边取对数，有：
\[\ln L=\ln \frac{M_p-M_1}{A}-\frac{E_a}{kT}\] 令\(a=\ln \frac{M_p-M_1}{A},b=\frac{E_a}{k}\)，有：
\[\ln L=a+bT^{-1}\] \(a\)和\(b\)为待定系数，通过试验数据进行拟合得到。

有些论文认为阿伦尼乌斯模型在高温下寿命的预测并不符合实际。

^{<span class="hint--top hint--rounded" aria-label="G. Li et al., "The Lifetime Prediction and Insulation Failure Mechanism of XLPE for High-Voltage Cable," in IEEE Transactions on Dielectrics and Electrical Insulation, vol. 30, no. 2, pp. 761-768, April 2023, doi: 10.1109/TDEI.2022.3215605.">[2]}中对交联聚乙烯(XLPE)电缆在120℃、140℃、160℃、180℃下进行了不同时间的加速寿命试验，并测试了试验后各样本的断裂伸长率（elonation at break），并认为\(M_p=50\%\)，即断裂伸长率为50%时线缆失效，利用实验数据进行线性拟合，得到了如下公式：
\[\ln L=13087.54\frac{1}{T}-24.90\]

逆幂律模型

在加速寿命试验中如果使用电应力，如电压、电流、功率等作为加速一般服从逆幂律关系模型。逆幂律关系模型说明，实体寿命与主要应力\(F\)的\(n\)次幂成反比关系：
\[t=CF^{-n}\] 其中\(C\)是一个常数。
考虑到电缆的加速寿命试验中可能会施加电应力，因此逆幂律模型也经常用于施加电应力的电缆加速寿命试验中。
大量的实验证明，电缆的寿命与其中通入的电流频率有关：电流频率\(f\)越高，电缆的寿命越短，因此有：
\[t=CF^{-n}f^{-x}\] \(x\)也是一个可调常数。

^{<span class="hint--top hint--rounded" aria-label="W. T. Starr and H. S. Endicolt, "Progressive Stress-A New Accelerated Approach to Voltage Endurance," in Transactions of the American Institute of Electrical Engineers. Part III: Power Apparatus and Systems, vol. 80, no. 3, pp. 515-522, April 1961, doi: 10.1109/AIEEPAS.1961.4501081.">[3]}中讨论了不同的电压和不同\(n\)下对建模的影响，以及根据作图预测\(n\)的方法。

Bahder等人认为线缆老化与电力线的局部放电(partial discharge)有关。
电缆的局部放电主要是由于绝缘部分被击穿而产生的电气放电，多发生在绝缘较弱的地方，可能是导体附近，也可能是其他部位。局部放电通常发生在绝缘层内或电缆表面的气隙中，这主要是由于固体和液体中介电常数大于空气中的常数，使得正常气压下固和液体介质的击穿电压高于气体，电缆周围的电场强度高于气隙中的电场强度，因此气隙更容易被击穿，产生放电，而其他部位仍可保持一定的绝缘效果，因此局部放电和布电现象出现。
对此，Bahder提出了基于逆幂律的数学模型，这个模型与通电频率、局部放电现象有关：
\[t=\frac{1}{fb_1\exp [b_2(F-F_0)-1](\exp [b_3F_b]+b_4)}\] 其中\(b_1-b_4\)都是可调常数；\(F_0\)是开始局部放电时的指标(the onset field required for discharges)；\(F_b\)是局部放电后线缆剩余的电气强度指标(the residual electric strength of the dielectric)。
实验证明，\(F\)-\(\ln t\)的关系中\(F\)的阈值不容易观察出来，在较长的时间尺度上逆幂律模型对寿命的描述并不好。

指数衰减模型

Dakin等人指出电器件的耐压特性(voltage endurance)呈指数衰减：
\[t⥋\exp \left[\frac{E-bF}{kT}\right]\] 其中\(b\)是常数；\(E\)是衰减过程的活化能。

在此基础上，一部分论文使用了另一种描述热应力的模型，称为艾林速率理论(Eyring rate theory)，该模型表示为^{<span class="hint--top hint--rounded" aria-label="J. . -P. Crine, J. . -L. Parpal and C. Dang, "A new approach to the electric aging of dielectrics," Conference on Electrical Insulation and Dielectric Phenomena,, Leesburg, VA, USA, 1989, pp. 161-167, doi: 10.1109/CEIDP.1989.69540.">[4]}：
\[L=\frac{h}{kT}\exp [\frac{ΔG}{k_bT}]\] 其中\(h\)为普朗克常量;\(ΔG\)是吉布斯自由能变(Gibbs free energy change),表示为：
\[ΔG=ΔH-T\Delta S\] \(ΔH\)为活化焓(activation enthalpy); \(ΔS\)为活化熵(activation entropy)。

进一步地，Endicott等人提出含有吉布斯自由能的一项可以表示为：
\[-\frac{ΔG}{kT}=\ln F (c+\frac{d}{T})\] 其中\(c,d\)为待定参数。
带入到艾林公式中，有：
\[t=\frac{h}{k_bT}F^{-(c+d)/T}\] 如此可以通过绘制图像拟合\(c,d\)的值。

事实上，如果认为\(n=(c+d)/T\),\(C=h/k_bT\)，那么也可以认为上述模型是一种逆幂律模型。但是实验证明这个模型的效果并不好。

Simoni在艾琳公式的基础上进一步修正，提出了线缆在高机械应力或者电应力的条件下的寿命预测，该方法认为寿命与应力强度\(F\)、开氏温度\(T\)，以及散射长度\(λ\)(scattering length，一个量子力学中的物理量，用于描述低能散射过程)等因素有关：
\[t⥋\frac{h}{2k_bT}\exp \left[\frac{\Delta G-eλF}{k_bT}\right]\] 基于上述理论，^{<span class="hint--top hint--rounded" aria-label="J. P. Crine, J. L. Parpal and G. Lessard, "A model of aging of dielectric extruded cables," Proceedings of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 1989, pp. 347-351, doi: 10.1109/ICSD.1989.69218.">[5]}提出了一种数学模型：
\[t=\frac{h}{kT}\exp \left[\frac{\Delta G-eλF}{kT}\right] csch\left[\frac{eλF}{k_bT}\right]\]

在上述式子中，如果\(F\)近似为0，那么其寿命预期将接近于无限。这一点与实验观测结果相同（如下图所示）。

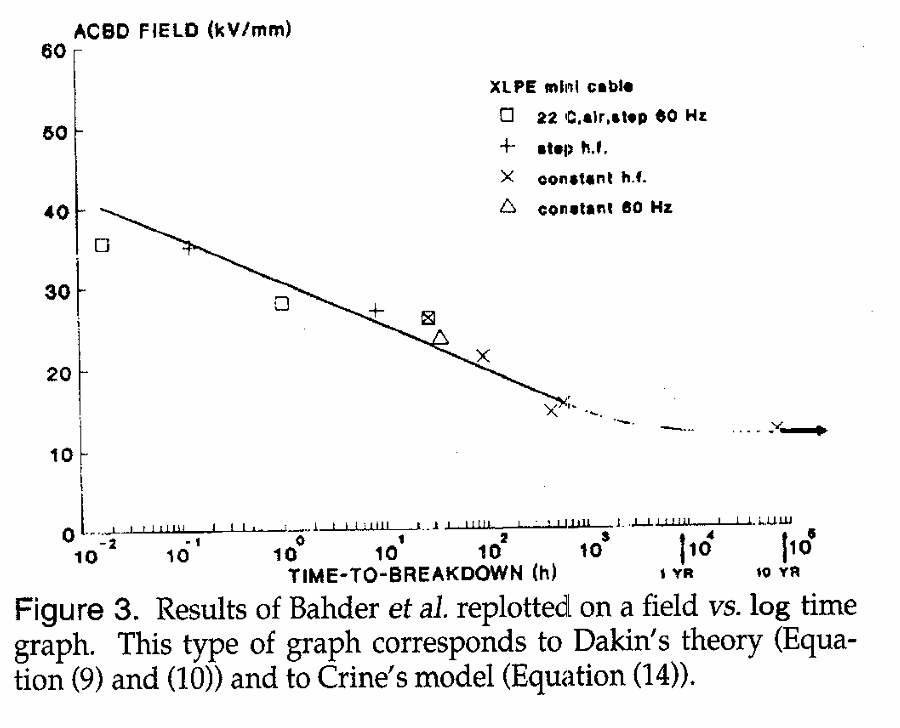
不过实际经验表明，电缆在非常低的应力下不会发生故障是不现实的。

总结

尽管逆幂律模型被广泛使用，但是它无法描述物理机制以及线缆在长时间的耐压试验的表现。
速率理论相比于简单的阿伦尼乌斯方程更好地描述了热老化，并且没有可调参数，而且描述了实验观察中较小应力下的寿命表现。

1. Chinh Dang, J. . -L. Parpal and J. . -P. Crine, "Electrical aging of extruded dielectric cables: review of existing theories and data," in IEEE Transactions on Dielectrics and Electrical Insulation, vol. 3, no. 2, pp. 237-247, April 1996, doi: 10.1109/94.486776. ↩︎
2. G. Li et al., "The Lifetime Prediction and Insulation Failure Mechanism of XLPE for High-Voltage Cable," in IEEE Transactions on Dielectrics and Electrical Insulation, vol. 30, no. 2, pp. 761-768, April 2023, doi: 10.1109/TDEI.2022.3215605. ↩︎
3. W. T. Starr and H. S. Endicolt, "Progressive Stress-A New Accelerated Approach to Voltage Endurance," in Transactions of the American Institute of Electrical Engineers. Part III: Power Apparatus and Systems, vol. 80, no. 3, pp. 515-522, April 1961, doi: 10.1109/AIEEPAS.1961.4501081. ↩︎
4. J. . -P. Crine, J. . -L. Parpal and C. Dang, "A new approach to the electric aging of dielectrics," Conference on Electrical Insulation and Dielectric Phenomena,, Leesburg, VA, USA, 1989, pp. 161-167, doi: 10.1109/CEIDP.1989.69540. ↩︎
5. J. P. Crine, J. L. Parpal and G. Lessard, "A model of aging of dielectric extruded cables," Proceedings of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 1989, pp. 347-351, doi: 10.1109/ICSD.1989.69218. ↩︎