遗传编程中的自动定义函数

参考资料：
John R Koza et al., Non-linear Genetic Process for Data Encoding and for Solving Problems Using Automatically Defined Functions, 1994.
John R Koza, Genetic Programming IV: Routine Human-Competitive Machine Intelligence, 2002.
John R Koza, Genetic programming III: Darwinian invention and problem solving, 1999.
John R Koza et al., Resue, Parameterized Resue, and Hierarchical Reuse of Substructures in Evolving Electrical Circuits Using Genetic Programming, 1996.
Cândida Ferreira, Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence, 2006.

GP和GEP中都有自动定义函数的机制，此处介绍的是Koza等人最初在遗传编程中提出的自动定义函数机制。

此处用“自动定义函数”表示这种机制，用“ADF”表示用这种机制产生的函数。

简介

许多计算机程序中都会有重复使用的程序结构，这些反复出现的结构可以被定义为一些包含形式参数(formal parameter)的函数，并在程序主函数中被调用，如此可以减少代码的长度。基于这样的思想，遗传编程(Genetic Programming, GP)中提出了自动定义函数(Automatically Defined Function, ADF)的机制，以减少不必要的计算量。
自动定义函数是一种参数化的、可以被层级结构组织并且反复使用的函数，它在进化的过程中随着整个种群共同进化。ADF作为一种特殊的函数被添加到构成种群个体的函数集(function set)中，和其他函数集中的函数一样被随机选择形成个体。在进化的评估(evaluation)阶段，含有ADF的个体会通过在树形结构被转义为计算机程序时通过调用函数(calling function)在相应的位置调用自动定义函数，并将ADF下层的端点和函数作为ADF的实际参数(practical parameter)引入到ADF中。
实验证明，引入自动定义函数机制后，计算量显著减少，并且个体的大小得到控制。

ADF的组织方式

含有ADF的个体结构

Koza等人在^[1]中定义了外部调用实体(external invoked entity)和内部调用实体(internal invoked entity)。外部调用实体指的是整个个体转义后得到的程序，它由若干个基函数(primitive function)，也就是用于生成初始种群的函数集中的函数、内部调用函数和端点组成，并且在使用内部调用函数的前提下，函数之间还具有一定的层级关系。
内部调用函数在这里指ADF，包括了基函数，形式参数(这里称之为dummy vairable)和可能的其他（或者自己，如此将形成递归）的内部调用函数。
按照功能划分，Koza等人在^[1]中由把含有ADF的个体结构分为两个部分：
第一段是结果生成部件(result-producing component)，这个部分可以看做是一个计算机程序的主函数，运行之后会产生相应的结果。一个个体需要产生多少个结果就需要拥有多少个结果生成部件，且至少需要一个结果生成部件以便进行评估。
第二段是函数定义部件(function-defining component)，这个部件用于生成ADF。
这两个部分通过连接函数进行连接，使得它们形成一个整体。由于最早的遗传编程的目的是为了自动生成LISP语言的程序，因此最早Koza等人使用的连接函数是LISP语言中的PROGN 函数，它的作用是将若干个函数一并运行。

需要注意的是，连接函数(linking function)这个概念是在GEP中被正式提出的，此处Koza等人使用PROGN函数组织个体的想法基本接近连接函数这个概念。

LISP语言中PROGN函数的使用可以参考：Blasting the PROG feature in Common LISP

在使用带有自动定义函数机制的遗传编程算法时，个体的拓扑结构需要被提前确定。具体而言，一个个体转义出来的程序中有几个结果生成部件和函数定义部件，以及彼此内部的层级关系是需要被提前确定的。

在结构变换操作(Architecture-altering Operation)加入之后，还可以用结构变换操作自动决定ADF的个数（也就是进化中会自我淘汰一部分ADF的子树结构）。

ADF的结构

由于ADF具有强类型(constrained type)特点，因此不同的ADF可能由不同的函数集和端点集生成。每一个ADF的结构包括三个部分：

• ADF的函数名
• 形式参数集合
  这个集合用于替代端点集生成ADF树形结构的端点。形式参数集合中形式参数的个数和具体哪一个形式参数会被用于生成某个特定的ADF都需要在运行前被提前指定。ADF使用形式参数的目的是为了让ADF在不同的环境和上下文中都能够编译运行。
  ADF可以不含有任何形式参数，这种情况有别于直接保存一个基因片段(Building-block)：ADF的树形结构是随着进化一同动态演化的，然而后者只是单纯的保存，无法做到动态演化。
  
• ADF具体的内容，表征为树形结构。

三个部分在LISP语言中通过DEFUN这个函数作为连接函数进行连接。DEFUN在LISP语言中的作用是定义函数。

下图展示了一个使用ADF函数的个体的树形结构（左）和程序框架（右）的例子。

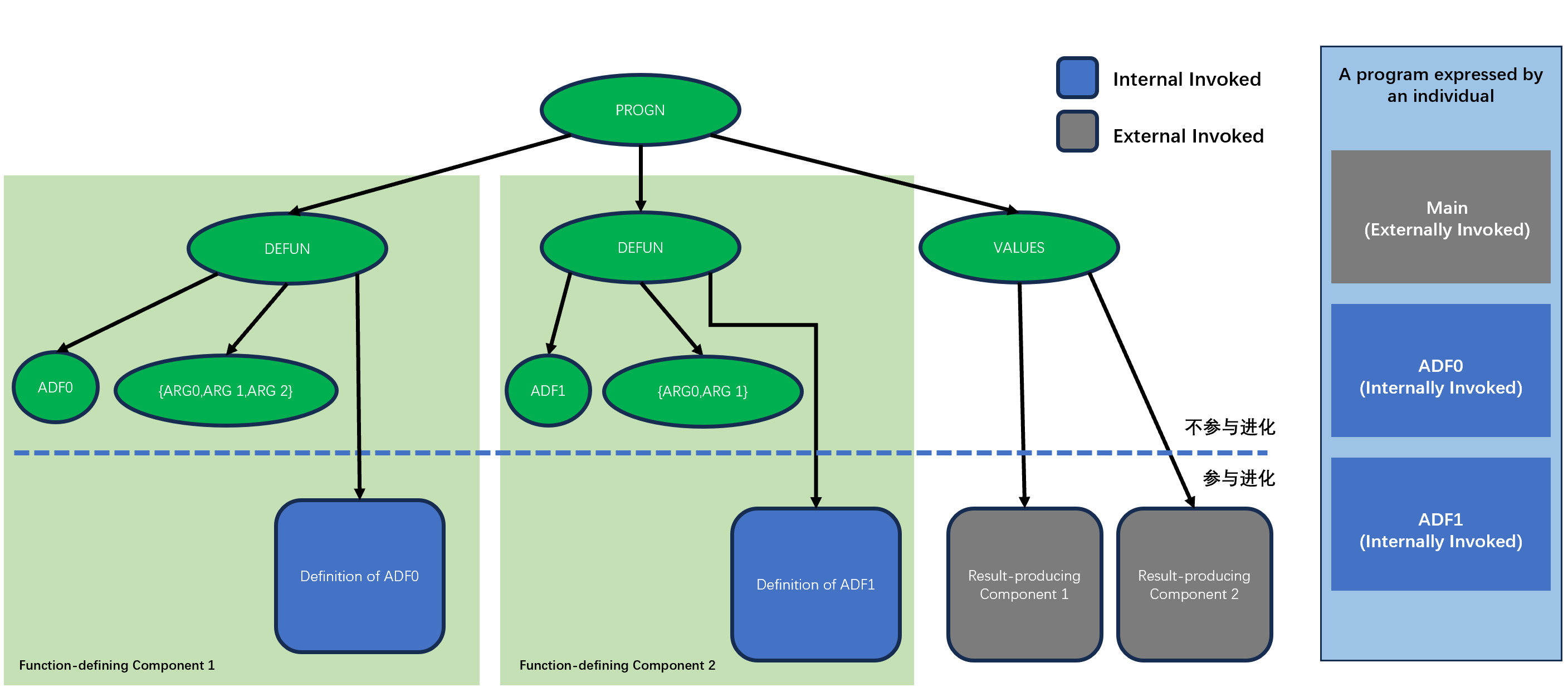
ADF的生成

尽管无需对生成的ADF的大小和结构做提前定义，但是在使用ADF机制时需要提前定义每个ADF中包含的形式参数数量和具体所使用的形式参数。
需要注意的是，指定的形式参数未必会真的被使用到某个ADF结构中，某个形式参数使用与否是由进化过程真正决定的。
一个ADF生成后，它可以作为用于生成别的ADF的成分添加到函数集中。

ADF的进化

个体评估中ADF的调用

在评估过程中，首先个体组成的外部调用程序（结果生成部件）会被适应度衡量(fitness measurements)程序调用，然后外部调用程序拉动内部调用程序。当ADF被调用时，形式参数会被实例化(instantiat)为声明(arguments)。也就是形式参数会被具体的值或者实际参数替代。实例化的调用可以使用两个相同或者不同的的实际参数或者是参数值、以及表达式。
下图展示的实例化都是被允许的。

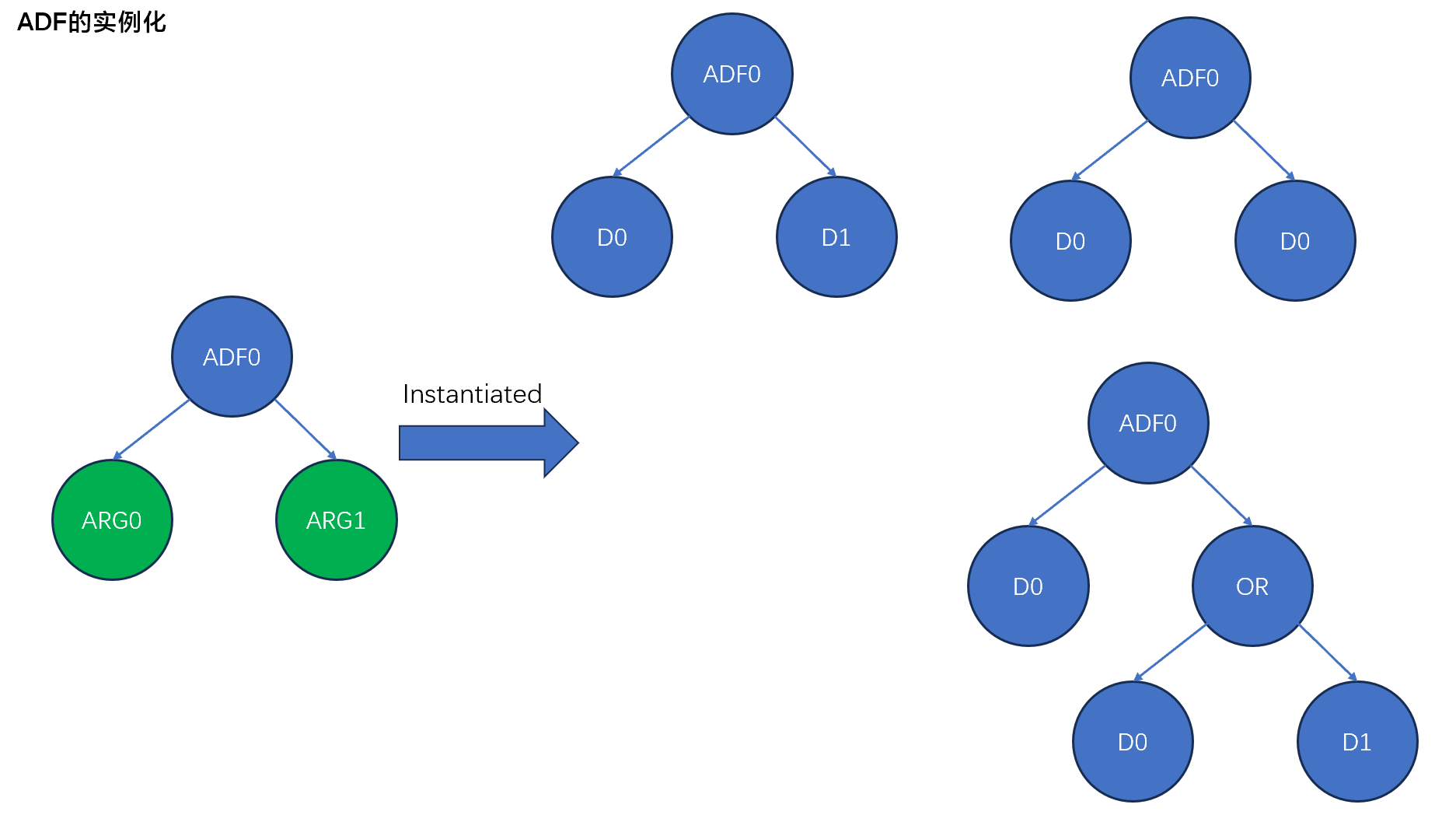
需要注意的是，ADF可以返回多个值，也可以不返回值。
为了节约计算量，在当前种群的评估过程中，每个ADF的函数定义部分只会运行一次而不是对每个个体都运行一次。

类保护的交叉和突变

带有自动定义函数机制的遗传编程中，ADF是随着每个个体一同进化的。
自动定义函数机制引入了一种称为“类保护”的交叉和突变(category preserving crossover and mutation)的机制，这种机制使得ADF可以自动进化，不断改进自身的结构。

同一类

在介绍这两种机制之前，首先要明确的概念是“同一类的”交叉/突变。
Koza等人定义的同一类的定义有两个：
第一种定义是：
如果：

1. 交叉/突变点在结果生成部件中。
   
2. 交叉/突变点在ADF中，两个ADF所使用的形式参数是完全相同的。（这两个ADF被视为同一类）

满足任意一个条件均视为被选择的两个交叉/突变点被视为是同一类的交叉和突变。

第二种定义是如果交换/突变和被交换/突变插入的部分同属一类，那么被选择的两个交叉/突变点被视为是同一类的交叉和突变。
在代码实现过程中，第一种定义的实现比较简单，所以通常使用的是第一种定义。

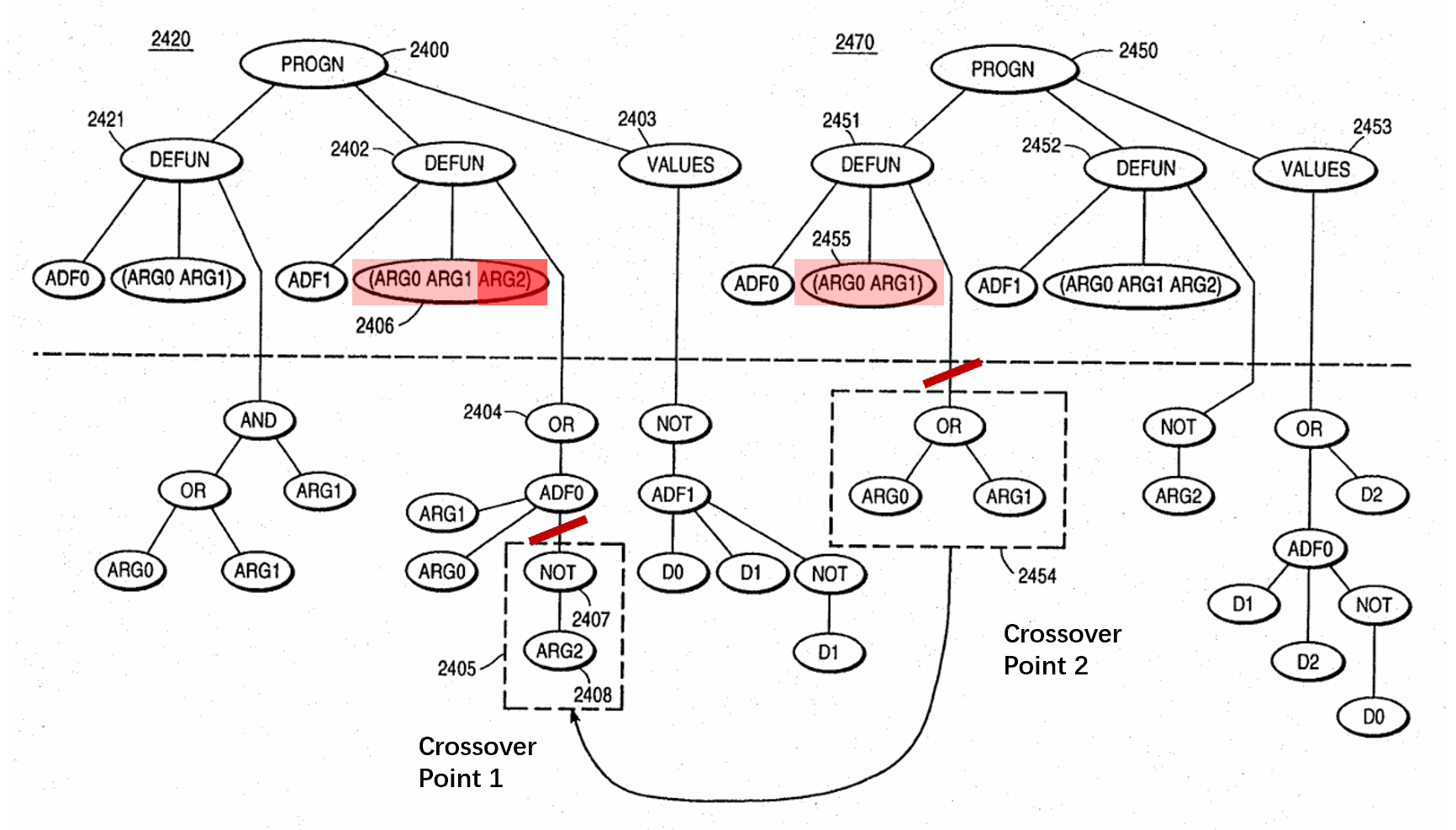
比如，对如上的两个个体2420和2470，如果两个交叉点分别选择在图示红线处，那么类保护交叉程序会检查的交叉对象主干的形式参数集合是否是同一个。此处个体2420的交叉点位于ADF1，其形式参数集合为\(\{ARG0,ARG1,ARG2\}\)，与个体2470交叉点属于的ADF0的形式参数集合\(\{ARG0,ARG1\}\)并不相同，于是类保护交叉不会发生。

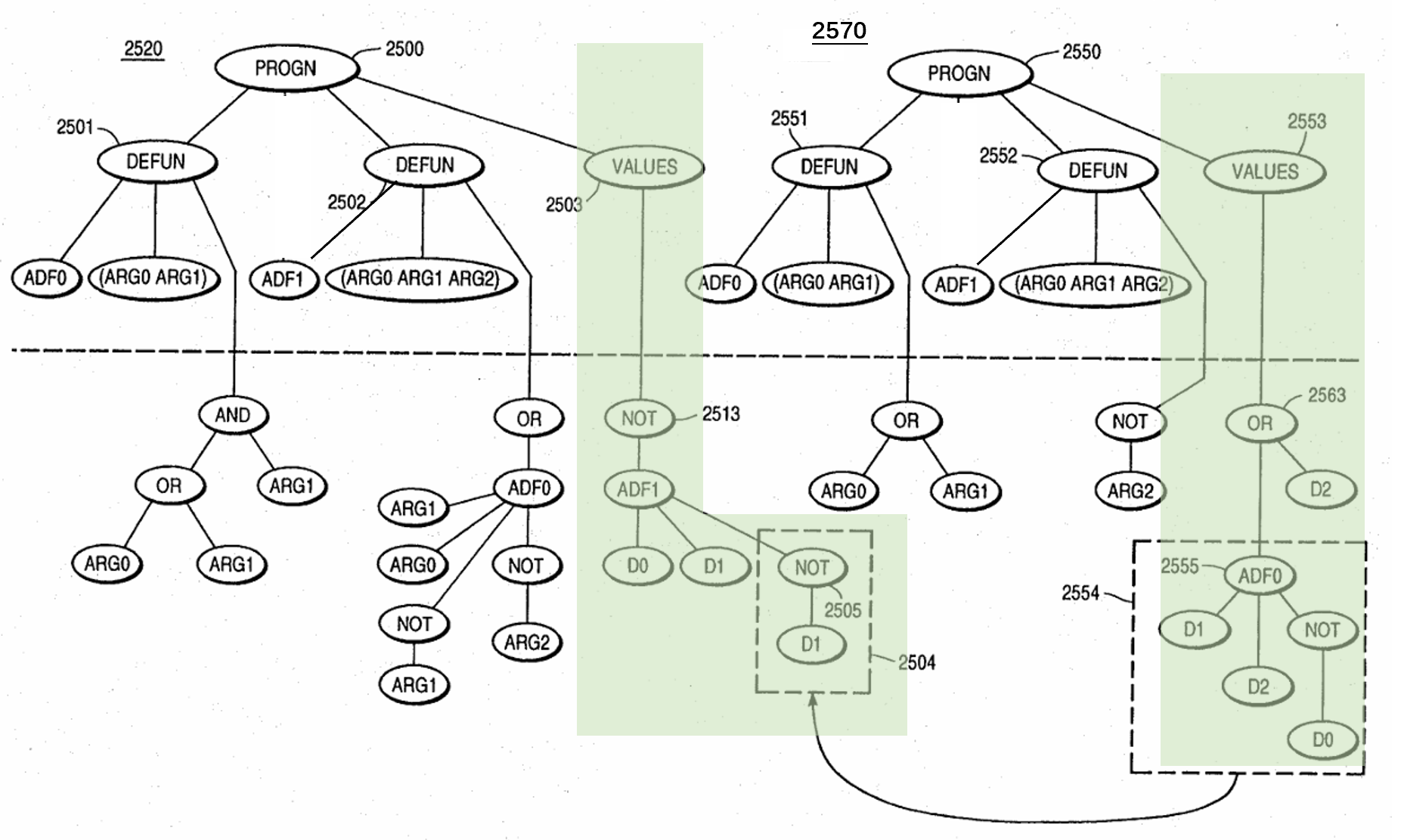
再比如，对如上的两个个体2520和2570，如果两个交叉点都发生在图示虚线处，那么类保护交叉程序会检查的交叉对象主干的形式参数集合是否是同一个。此处个体2520和2570的交叉点都位于结果生成部件当中，因此两个交叉点属于同一类。类保护交叉将会发生。

类保护的

类保护的交叉和突变只能够在同一类中进行。从另一个角度看，也就是说只有从同一个形式参数函数集合中生成的ADF之间可以做交叉和突变。更进一步的解释是，不同类别的ADF之间的进化是完全独立的。

实现

类保护的交叉的实现是，首先随机选择一个交叉点，再随机选择第二个交叉点，如果第二个交叉点和第一个交叉点不属于同一类，那么重新随机选择第二个交叉点直到找到符合条件的交叉点。
类保护突变的实现是，首先随机选择一个突变点并且随机生成一个子树，然后检查被插入的生成的子树在此处是否有意义。如果没有意义则重新生成子树。
从此处可以看出，使用自动函数生成机制的进化过程是相当冗杂的，根据其后^[2]的评述，这样搜索的失败率非常的高。交叉和突变非常容易找到不属于同一类的交叉和突变点，然后重试。

ADF的实现

避免递归的实现方式

最后一点需要说明的是，虽然允许ADF调用其他ADF是可以将问题分层分解为一个个层级性的函数结构，但是在最一般的形式中，允许自动定义的函数调用其他同一类类函数将导致重复引用。为便于解释，在所示示例中不允许自动定义函数之间的递归引用。由于基因生成的实体经常是问题的错误解决方案，如果允许任何自动定义的函数引用自身，就必须预见无限递归的可能性。
因此需要设计机制避免出现无限递归。
第一种方法是按照ADF的生成顺序，有序地加入其他ADF的函数集。比如在生成第一个ADF，ADF0时，ADF0所使用的函数集就是基函数集合\(\mathcal{F}_{ADF0}=\mathcal{F}\)。然后第二个生成的ADF，ADF1使用的函数集是：\(\mathcal{F}_{ADF1}=\mathcal{F}⋃\{ADF_0\}\)，然后第三个生成的ADF2使用的函数集是：\(\mathcal{F}_{ADF1}=\mathcal{F}⋃\{ADF_0\}⋃\{ADF_1\}\)，以此类推。

第二种方法比较复杂，是使用程序检查非环引用：也就是从函数定义到函数调用的路线中过程不允许循环引用。

有观点认为不应该避免递归调用，但是递归调用的好处仍然需要调查。

评价

对遗传编程中的自动定义函数，Candida Ferreira在^[3]中指出具有如下的不足：

• GP中的ADF彼此之间无法通过遗传操作交换遗传信息。
  
• ADF中形式变量的个数需要被提前确定，引入了更多的先验知识。 而且形式变量的数量限制了ADF对目标的表达。

尽管Koza等人声称ADF可以通过只运行一次重复过程来减少计算量，但是该过程也可以同样通过记录计算结果实现。
但是事实上ADF的调用只是单纯的把子树打包，无法缩减个体的“实际”大小。

1. John R Koza et al., Non-linear Genetic Process for Data Encoding and for Solving Problems Using Automatically Defined Functions, 1994. ↩︎
2. Ferreira, C., 2001. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. Complex Systems, Vol. 13, issue 2: 87-129. ↩︎
3. Cândida Ferreira, Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence, 2006. ↩︎