03. 控制器的自动综合

控制器的自动综合

这是对《Genetic Programming IV: Routine Human-Competitive Machine Intelligence》的笔记，本页对应第三章： Chapter 3： Automatic Synthesis of Controllers.
这一章讲述了如何使用遗传编程完成控制器的自动设计。

原书的免费公开版本在作者Koza本人的Research gate主页上：https://www.researchgate.net/publication/243776894_Genetic_Programming_IV_Routine_Human-Competitive_Machine_Intelligence
这本书也可以在Springer 购买电子版： https://link.springer.com/book/10.1007/b137549
或者在亚马逊英国购买纸质版： https://www.amazon.co.uk/Genetic-Programming-IV-Human-Competitive-Intelligence/dp/0387250670

人类工程师进行设计的过程涉及到对各种考量的权衡，因此可以说设计的过程是需要使用到人类的智能的。这一章讲自动设计控制器(controller)作为例子讲述遗传编程在设计领域的应用，这一章包括了使用遗传编程设计如下的控制器：

• 二阶滞后补偿器
  
• 三阶滞后补偿器
  • 带有时延的三阶滞后补偿器
    
• 非最小相位系统

控制器背景

控制器原理

使用控制器的目的是为了让系统原型(plant)、也就是控制器控制的目标系统的响应能够与一个设计者所期望的响应尽可能的匹配。此后作者举了一个控制车速的巡航控制器(cruise control device)的例子来说明控制器是如何工作来控制系统的。简单来说，控制器对系统的作用不是一蹴而就的，而是需要时间让整个系统不断调整自己的输出。在控制器控制系统原型的过程中，控制器需要通过监控系统原型的输出，并且比较和参考信号(reference signal)之间的误差(error signal)来调整原型系统的输入，从而让整个系统的输出你能够更加贴近参考信号。这样通过接收输出、改进输出、再将改进后的输出作为输入的控制方法称为反馈控制(feedback control)。如果反馈控制通过误差信号作为原型的下一次输入，那么这样的反馈控制称为负反馈控制(negative feedback control)。
含有反馈的控制系统也称为闭环控制系统（closed-loop control system），输入与反馈信号比较后的差值（即误差信号）加给控制器，然后再调节受控对象的输出，从而形成闭环控制回路。所以，闭环系统又称为反馈控制系统，这种反馈称为负反馈。与开环系统相比，闭环系统具有突出的优点，包括精度高、动态性能好、抗干扰能力强等。它的缺点是结构比较复杂，价格比较贵，对维修人员要求较高。

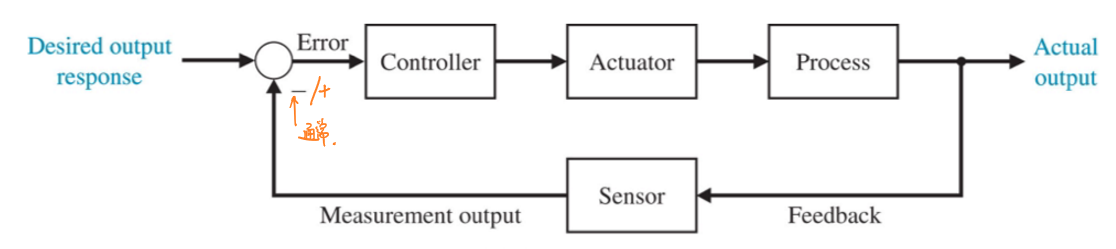
更多关于控制论的内容请参考学习笔记中的控制系统课程。

现实世界当中大部分的控制器都是手动的（比如阀门、手动控制的开关等等），但是这本书中强调的控制器都是自动控制器，也就是自动根据反馈输入调整系统输出的控制器。

控制器的设计指标

在设计时需要考虑的控制器的特征非常多，下面列出了常见的一些控制器的设计指标，这些指标都和系统的阶跃响应有关(step response，指系统输入为单位阶跃信号时系统的时域输出变化)。

• 上升时间和调节时间
  设计控制器的过程中最常见的考虑因素是让系统响应表现为理想响应的时间尽可能小。这一设计指标通常被诠释为上升时间\(t_r\)（rise time）或者是调节时间\(t_s\)(settling time)。
  上升时间是指定义为阶跃响应曲线从稳态值的10%第一次上升到90%所需的时间。
  调节时间是指阶跃响应达到并永远保持在一个允许误差范围(误差带：通常取±5%或±2%)内，所需的最短时间。

• ITAE
  控制工程中喜欢使用参考信号和系统原型的响应之差的绝对值在时间上的积分(the integral of the time-weighted absolute error)来衡量控制器的性能。由于按照时间的加权中会对比较晚出现的误差有更大的惩罚、应用ITAE作为适应度有助于迅速减小误差。

• 过冲率
  过冲率\(M_p\)(overshoot)是指的系统原型的响应超出参考信号的最大百分比。过冲会消耗大量能量，设计时需要尽可能的考虑减小过冲。

• 鲁棒性
  在现实中还会出现干扰（disturbance）。这种干扰对系统的影响通常被建模为在系统原型输出端的加性噪声。鲁棒性可以表示为系统对于噪声的灵敏度，即系统输出对噪声的偏微分：
  \[\frac{∂S_{output}}{∂N}\]
  好的控制系统可以对噪声表现出高鲁棒性，也就是输出对噪声的灵敏度不高。

• 稳定性
  稳定性(stability)是指系统随着输入信号微小变化的响应程度。如果整个系统的性能随着系统原型的微小变化而变化很大，那么这个系统可能毫无用处甚至会有危险。

这些设计指标在系统的阶跃响应图上表现如下：

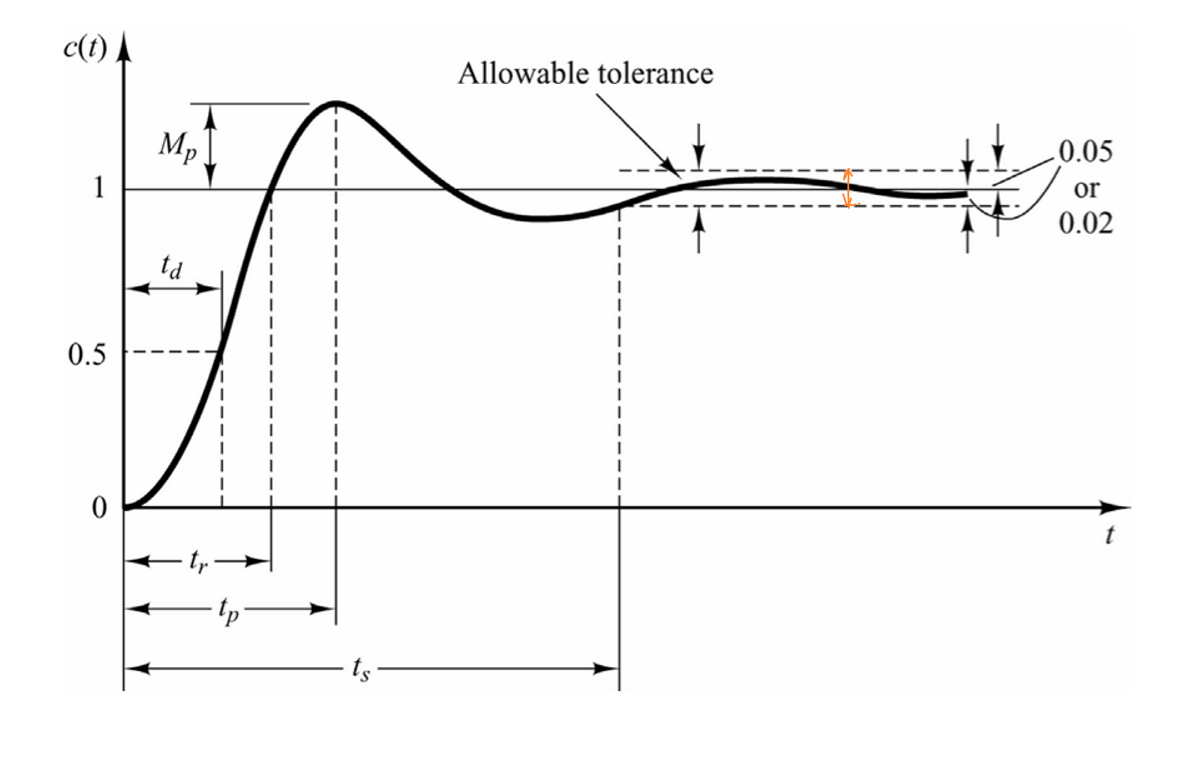
控制器的基本组成

一个控制器电路通常可能会用到如下的器件：
放大器(gain)、积分器(integrator)、差分器(differentiator)、加法器(adder)、减法器(substractor)、超前补偿(laed)、滞后补偿(lag)、延时器(delay)、翻转器(invertor)、取绝对值(absolute)、限制器(limitor)、乘法器(multiplier)、分配器(divider)、开关(switch)。

控制器的拓扑结构可以描述为：

• 控制器内部用到的器件数
• 用到的器件类型
• 控制器内部器件的输入和输出的连接方式
• 控制器的外部输入和外部输出

PID控制器

PID控制器是控制系统中最常用的控制器类型，它由基本的三个控制器：P控制器、I控制器、D控制器组成。

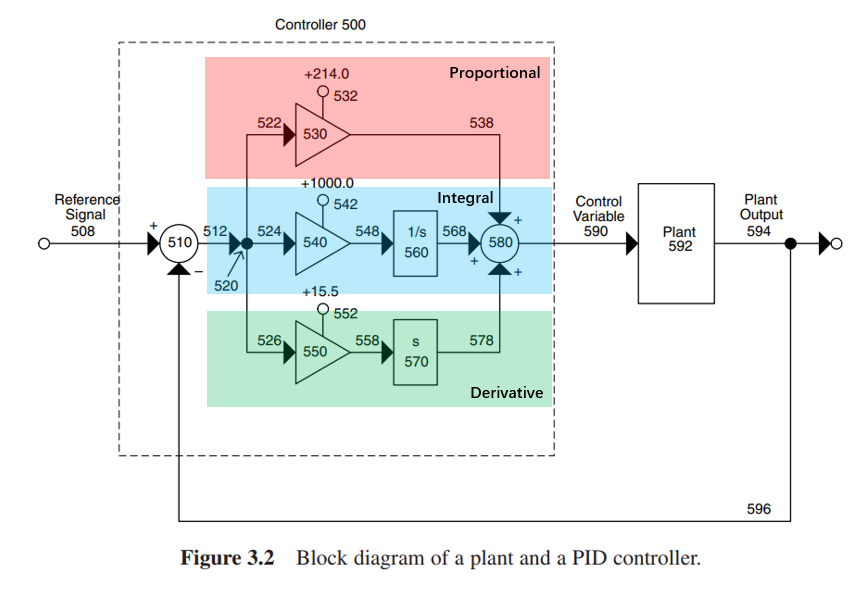
三个部分都对PID控制器整体的输出有对应的贡献。

• P控制器(proportional controller)，又称为比例段，它的作用是将参考信号和原型系统的输出之间的误差直接反馈给系统。
  
• I控制器(integral controller)，又被称为积分段，它的作用是使得控制器在稳态时候的误差更小。
  
• D控制器(derivative controller)，又被称为微分段。由于比例段提供的误差补偿总是滞后的，利用这一点P控制器可以通过求误差信号的斜率来预测未来误差信号的变化情况。

PID控制器的作用用PID控制器的发明者Callender和Stenvenson的说法是：
“本发明的一个具体目的是提供一种系统，该系统将产生一种补偿效果，该补偿效果受与偏差的总范围、偏差率和给定期间内偏差的总和成比例的因素所支配。”
> A specific object of the invention is to provide a system which will produce a compensating effect governed by factors proportional to the totoal extent of the deviation, the rate of the deviation, and the summation of the deviation during a given period.

尽管PID控制器在现在的工业界应用非常广泛，但是对更好的控制器的需求从来没有停止过。在Astrom和Hagglund(1995)的论文中提到，只有20%的控制器工作的比较好。

控制器的智能设计方法论

智能设计方法总述

对控制器的智能设计，或者说智能综合需要设同时计控制器的拓扑结构和相应的参数的值，来满足用户指定的高阶的设计需求。下面列出了一些常见的对设计需求的高阶表达：

• 优化要求
  比如最小化ITAE
  
• 时域要求
  比如最小化过冲、最大化抗噪性等等
  
• 频域要求
  比如系统带宽、随着噪声的衰减等等
• 稳定性要求
  
• 鲁棒性要求
  
• 对特定信号的值的限制

在后续，

用传统的设计方法（比如说状态空间设计、根据波特图的设计等等）很难同时满足上述几个设计要求的任意组合，因此需要使用到智能算法来进行优化。下面的几种启发式的方法可能可以解决这样的设计要求：

• 爬山算法 (hill climbing)和基于梯度的算法(gradient methods)
• 模拟退火算法(simulated annealing)
• 进化计算(*这本书写作之时还没有进化计算这个概念，原书中写的是evolutionary methods)

上述的这些方法都是启发式学习的方法，这些方法的迭代操作都类似，高层级的语言表示如下：

1. 从搜索空间中的一个或者几个点上开始搜索，衡量这一个或者几个点的表现
   
2. 通过改变现有的搜索点的结构来创建新的备选点
   
3. 衡量新的备选点的表现，并得到一个指标
   
4. 用这个指标对备选点进行选择
   
5. 重复上述操作

整个人工智能算法大致可以分为两类：启发式学习（又分为构造算法和改进算法，改进算法中包括了贪心算法和非贪心算法）和精确方法(比如专家系统、统计回归等等)。

不管是何种搜索算法，搜索行为的主要动力来源于对个体表现的衡量，用于衡量的函数以代价的形式（越低越好）或者以适应度的形式（越高越好）出现。并且通常新的个体是基于现有的个体产生的，下面将详述这几种算法的搜索行为。

爬山算法和基于梯度的算法

爬山算法开始于整个搜索空间的一个个体，对这个个体指定适应度后再创建新的个体，指定这个新的个体的适应度，然后通过适应度的衡量决定选择原来的个体还是新创建的个体。新个体的创建方式依照问题的不同而不同。
梯度下降可以看做是使用梯度作为适应度衡量的爬山算法。
爬山算法是一种点对点的贪心算法。在每一个循环中，爬山算法会无条件拒绝没有任何改进的个体，同时也会无条件接受具有改进的个体。(*形象的形容为：猴子搬玉米)在单次尝试当中，爬山算法容易陷入局部最优。如果问题允许多次尝试，那么多次尝试可能会找到全局最优。但是每一次尝试都是独立的，新一次的搜索并不会继承原来的搜索(*找不找得到全凭运气)。
爬山算法的另一个问题是并行化，虽然有并行化的爬山算法，但是并行线程之间的工作是独立的，并没有信息交流。

遗传算法并行化过程的信息交流参考并行遗传算法

模拟退火算法

模拟退火算法也是一种点对点的搜索算法。这种算法也使用了一种特定问题的修改操作来基于现有个体产生新的个体，但是与爬山算法和梯度下降算法不同的是，模拟退火算法中使用了Metropolis算法和玻尔兹曼算法来来决定是否保留那些没有任何改进的个体。
此外，模拟退火运用了一个变量温度(temperature)\(T\)来控制算法的运行过程和收敛情况，\(T\)在运行过程中指数单调递减，并且影响Metropolis算法和玻尔兹曼算法对个体是否保留的抉择。在\(T\)很高的时候，算法更倾向于接收那些没有任何改进的个体，随着算法迭代次数的增加，\(T\)很低的时候，算法更倾向于拒绝那些没有任何改进的个体，以加快算法的收敛，但是为了保证全局性，算法也不会完全拒绝任何个体。

进化计算

进化计算的搜索方法并不是贪心的，而是一种全局的搜索方式。并且，进化计算的操纵对象是群，因此是一种群智能搜索方法，而非点对点的搜索方法。在运行过程中，进化计算会在一开始会产生大量的个体，但是在趋于收敛时只有一小部分的个体生成。
遗传编程对于控制器的设计方法会在之后详述。

使用遗传编程的自动控制器综合方法

这本书中的控制器设计方法包含对拓扑和器件参数两方面的设计，包括：

• 建立一种可以被遗传编程逐步解读的个体表示的方法
  
• 设计一种可以诠释高层级设计需求的适应度评估方法

遗传编程中树的进化方法

本书的作者想出了三种针对控制器设计用树形结构来表达个体的方法。

• 第一种方法是每个个体代表一种指示构建的方法，也就是说个体并不直接操纵电路，而是将个体编写为操纵电路的指令或者程序，由翻译好的程序对电路进行搭建。在这种方法下，程序的不同部分的运行顺序需要有先后：ADF需要先运行，然后再运行主程序。
  
• 第二种方法是首先考虑设计出一个基板电路(embryo，*这里作者用了生物学的胚胎指代基板电路，那么个体的操作可以认为是对这个胚胎的发育过程，从而将胚胎发育成完全发育的结构)，这个基板电路上有一些可以被指令操纵的结点。遗传编程中的每个个体代表一种修改这个基板电路的方式。通过将程序树中的函数逐步应用于基板电路结构，从而将基板电路变成完整的可以实现功能的控制器电路。与第一种方法一样，程序中的函数按照指定的评估顺序分别执行。
  
• 第三种方法是每一个树代表一种控制器电路的连接方式，函数节点为各种电路器件，从而直接将树转化为整个控制器电路。这种方法没有先后运行的顺序。

本书在设计中用到的是第三种方法。如此，进化过程中个体会被直接翻译为控制器电路，然后带入仿真软件中运行，最后将仿真的特性作为个体的适应度。

基函数集、端点集和强类型

基函数集

设计中用到的基函数及其功能如下表所示：

器件	功能	数学表达	参数
GAIN	用一个常数放大时域信号	\(Asin(ωt)\)	1. 常数 2.时域信号
INTEGRATOR	时域上对一个信号进行积分 在频域上对信号乘\(1/s\)	\(\int Asin(ωt) ⇔\frac{1}{s}[S]_s\)	1.时域信号
DIFFERENTIATOR	对时域信号作差分 为表示简便，在频域上对信号乘\(s\)	\(s[f]_s\)	1.时域信号
ADD_SIGNAL SUB_SIGNAL MULT_SIGNAL	分别对应对信号的加减乘一个常数	\(f_1 [·] f_2\) \([·]∈\{+,-,×\}\)	1. 时域信号 2. 时域信号
ADD_3_SIGNAL	三个时域信号相加	\(f_1+f_2+f_3\)	1. 时域信号 2. 时域信号 3.时域信号
DIFFERENTIAL_INPUT_INTEGRATOR	时域上对两个信号的误差积分	\(∫(f_1-f_2)dt\)	1. 时域信号 2. 时域信号
INVERTER	反转信号	\(-f\)	1.时域信号
LEAD	频域上与\(1+τs\)相乘	\((1+τs)[f]_S\)	1.时域信号 2.常数\(τ\)
LAG	频域上与\(1/1+τs\)相乘	\(\frac{1}{1+τs}[f]_S\)	1.时域信号 2.常数\(τ\)
LAG2	频域上与\(ω_0^2/s^2+2ζω_0s+ω_0^2\)相乘	\(\frac{ω_0^2}{s^2+2ζω_0s+ω_0^2}[f]_S\)	1.时域信号 2.常数\(ω\) 3.常数\(ζ\)
ABS	对时域信号取绝对值	\(\lvert f \rvert\)	1.时域信号
LIMITER	限制信号在某一区间	\([f]_{capped}\)	1.时域信号 2.下界 3.上界
DIV	两个时域信号相除并限制	\([\frac{f_1}{f_2}]_{capped}\)	1.时域信号 2.时域信号 3下界 4.上界
DELAY	对信号进行时延	\([f]_se^{-sT}\)	1.时域信号 2.时延\(T\)
IF_POSITIVE	开关，运算结果为正时输出某个声明，反之输出另一个声明	\(\begin{cases} f_1, f_0>0 \\ f_2,f_0 ≤0\end{cases}\)	1. 时域信号 2. 时域信号 3.时域信号
+,-,×,÷	数值运算	-	1.常数 2.常数

此外还有ADF。

端点集

端点集中包括了如下的端点：

标识	意义	类型
REFERENCE_SIGNAL	参考信号	信号
PLANT_OUTPUT	系统原型的输出	信号
CONTROLLER_OUTPUT	控制器的输出信号	信号
STATE_0,STATE_1,...	系统的内部状态	信号
CONSTANT_0	恒定为0的信号，用于干扰遗传编程，展示用	信号
\(\mathfrak{R}\)	实数	实数

强类型

强类型是值和拓扑结构实现统一进化最关键的机制。每个个体表达的树中的函数集和端点集分类如下：

• 信号处理函数
• ADF
• 表示时域信号的端点
• 用于表示算术子树的端点和函数（算术子树用于进行数值运算，在下面会详细解释）

系统原型的表示

如果系统原型的结构是设计者可以了解到的，那么控制器的行为和特点可以通过仿真系统原型和控制器一并得到。如果原型结构无法被了解（*黑盒），那么遗传编程可以根据原型的输入输出生成一个符合的系统原型，再与控制器一并仿真。

自动定义函数在设置控制器上的使用

在这个设计任务中，ADF不止可以通过重用函数来节省计算量，更重要的是ADF可以表示电路的两种结构：

• 并联结构
  ADF可以视作是打包好的字电路。由于重用，ADF函数的输出信号可以传递到不同的模块中，这就相当于是电路的并联。
  

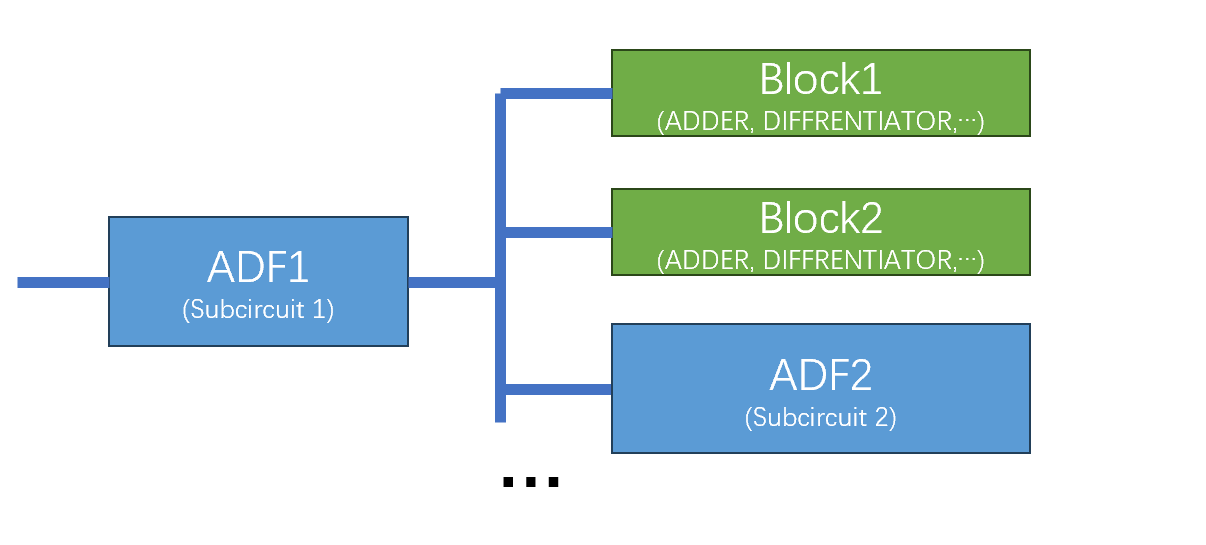
  如果不使用ADF的话，可以在函数集中添加一个表示并联的函数来实现并联。

• 反馈结构
  ADF的递归结构可以视为是将上一次ADF的输出又重新返回到ADF的输入中，这样的操作在电路中是一种内部反馈。
  

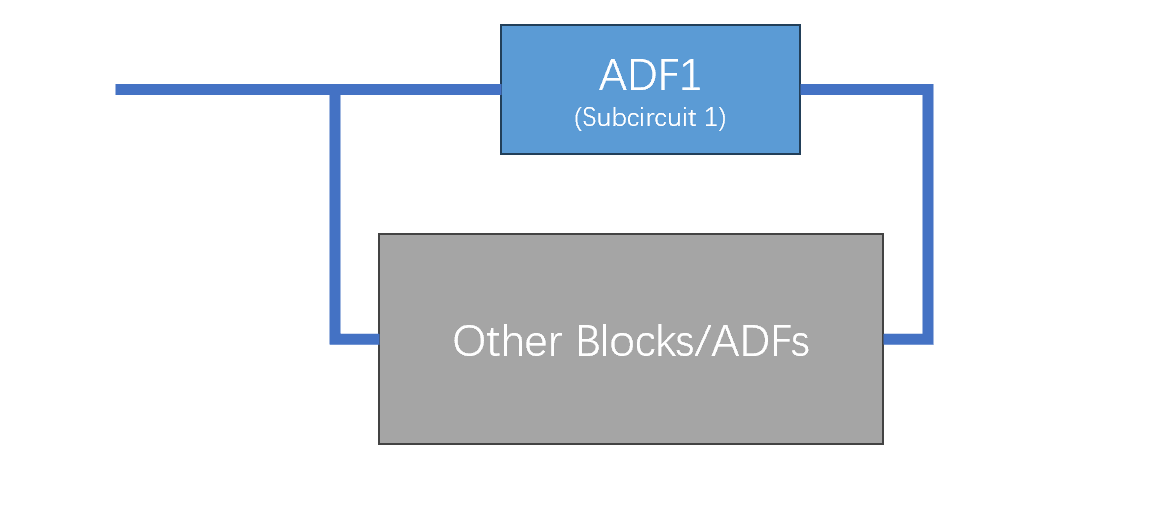
调试器件参数的方法

如之前所说，对控制器的设计包括拓扑结构的设计和器件参数调试两方面。器件之间的拓扑结构可以通过树内部的端点和函数的连接来表示，但是在进化过程中演化器件拓扑结构的同时调整器件参数却并没有那么容易做到。这本书中介绍了三种进化过程中同时达成这两个目标的方法。需要注意的是，这三种方法都需要借助强类型实现。

算数子树

第一种方法是：使用一种专门进行算术演算的子树结构，书中称为算术子树(arithmetic-performing subtree)，这种子树结构包含多个数值运算的函数并以自然常数作为端点。
具体而言，第一种方法下，端点上的数值从\([-5,5]\)中选择，这个值在某个个体中被确定之后，在这个个体的运行过程中将不再发生变化。这个端点的值在运行过程当中使用非线性映射(NLM,none-linear mapping)转化，并在算数子树的运行过程中表达。
对数形式的非线性映射可使相差几个数量级的常数得到有效进化。除非另有说明，本书中使用的非线性映射将-5到5之间的数值转换为超过 10 个数量级的数值。
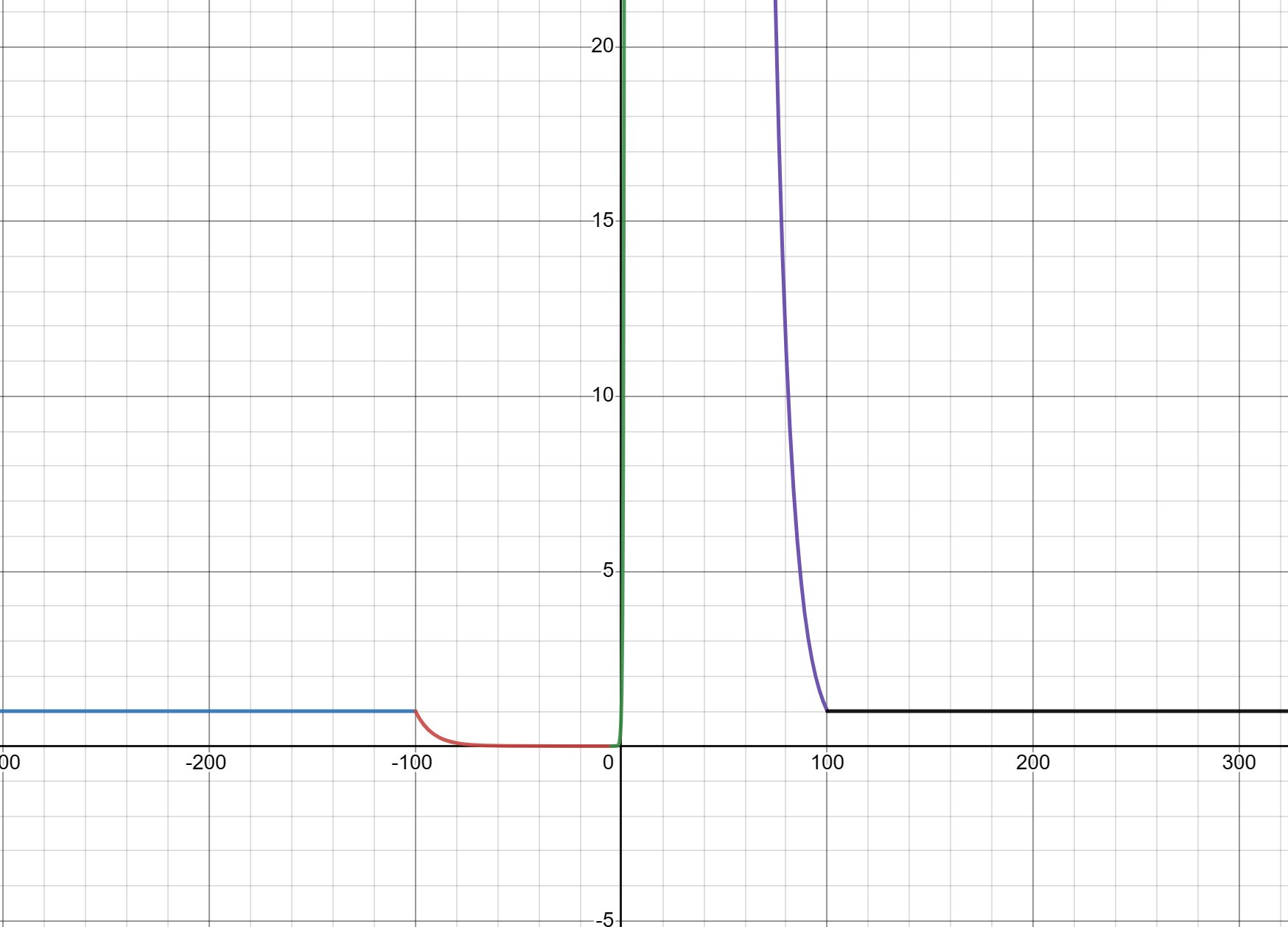
一个非线性映射函数的例子如下：
\[NLM(x)=\begin{cases} 10^0,\text{ if }x<-100\\ 10^{-\frac{100}{19}-\frac{1}{19}x},\text{ if }-100≤x<-5\\ 10^x,\text{ if }-5≤x≤5\\ 10^{\frac{100}{19}-\frac{1}{19}x},\text{ if }5<x≤100\\ 10^0,\text{ if }x>100\\ \end{cases}\] 从图像上可以看出，这个函数的作用是成倍放大-5到5之间的\(x\)的值。

此处使用非线性映射的原因个人认为是原本的搜索空间太过稀疏造成的。使用非线性映射可以让之前的搜索在一个较为均匀的搜索空间中进行，然后在放回到原来稀疏的空间中。

因此目前掌握的让搜索空间更加均匀的方式有三种：

1. 从个体编码的设计上让各个信息在空间中均匀分布
   
2. 使用排名
3. 使用映射函数

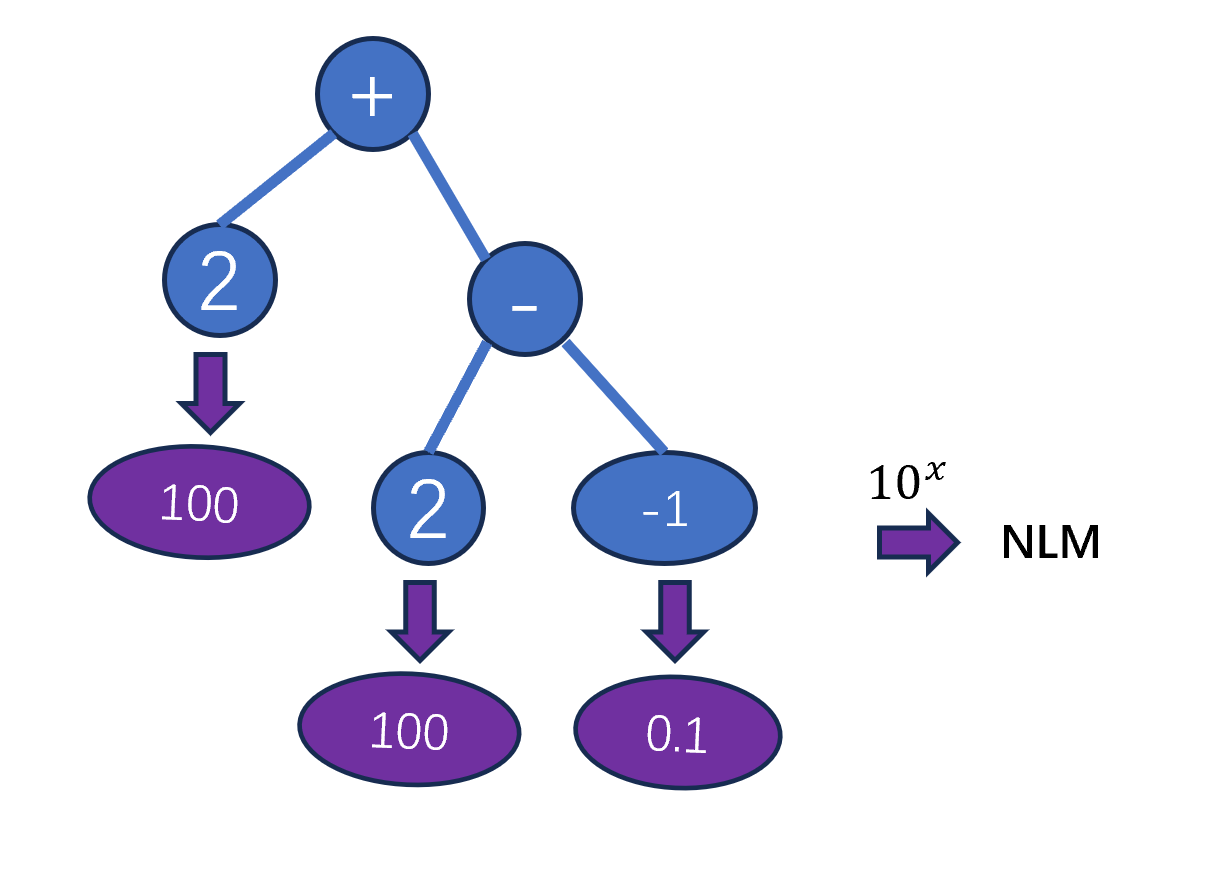
使用第一种方法加上参数变换操作的控制参数设置如下：

参数	值
单后代交叉	86.5%
复制	10%
普通突变	1%
子程序复制	1%
子程序创建	1%
子程序删除	0.5%

第一种方法被认为效率较低，原因是算树子树的交叉是一种近似于随机突变的操作。

需要注意的是，使用算数子树虽然搜索的进程并不是直观的，但是从结构上仍然应当是在逐步逼近期望的值的结构。但是本书的作者认为这种方法下在搜索空间中每一次搜索的跳变太大了。
但是究竟跳变有多大，并没有一个实际的度量。这种情况下一种个人觉得可行的方法是将每个节点看做变量对适应度函数求偏微分得到该处跳变的灵敏度。

可扰数值

第二种方法是，子树中直接将可扰数值(perturbable numberical value)作为一个节点。所谓可扰数值是指该数值为从某个正态分布（书中方差为1，均值跟随进化）中的一个抽样。
具体而言，在第0代中的数值端点都会随机地从\([-5,5]\)中选择，然后在接下来迭代中这些值会被施加按照以该值为均值，方差为1的一个正态分布中所抽样的一个值替代。在表达时同样使用非线性映射。此后这种方法使用了一种特殊的突变方式，称为高斯突变(Gaussian mutation)。在整个搜索过程中，这个些端点的值的变化并不会非常大。

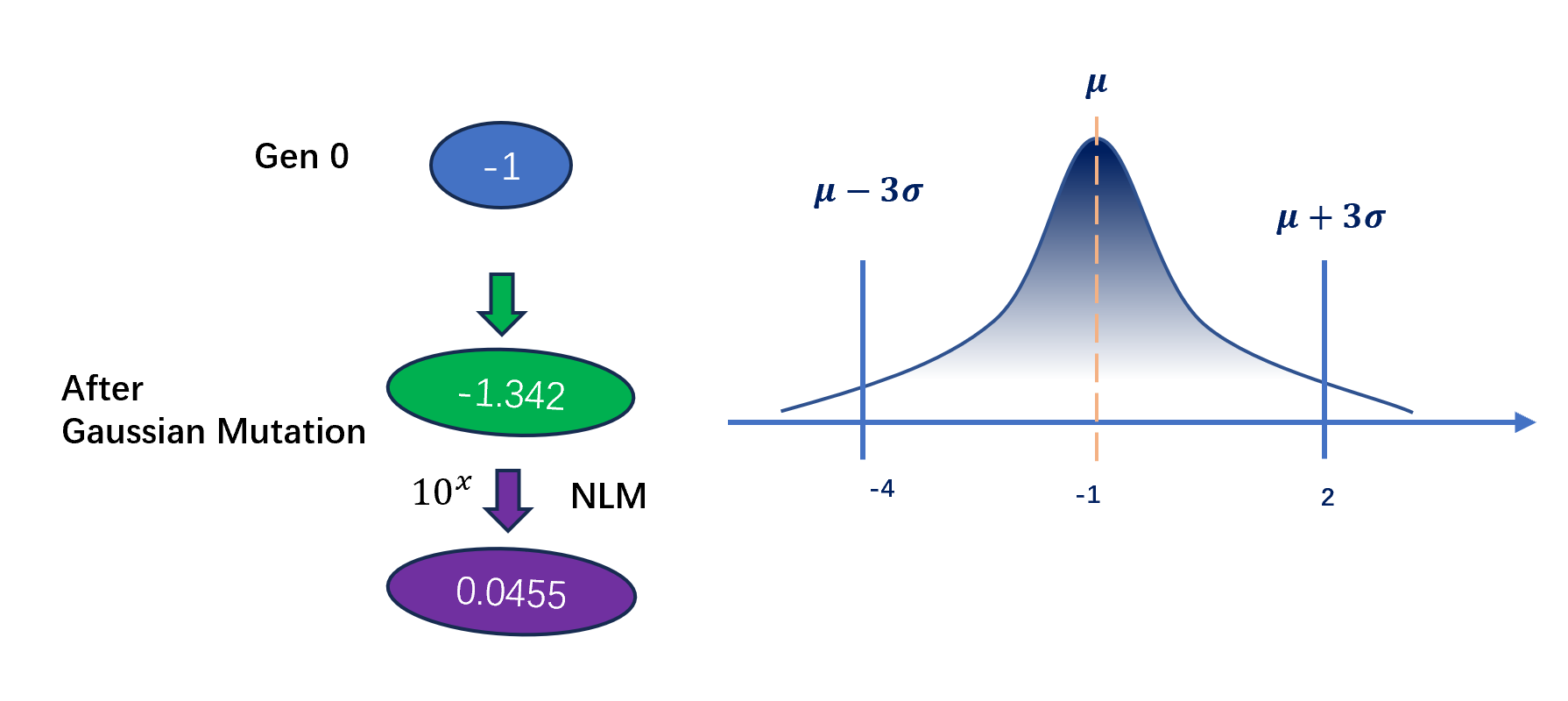
使用可扰数值的原因个人认为是为了控制突变造成的影响。

使用第二种方法的控制参数设置如下：

参数	值
对可扰数值的高斯突变	20%
对除了可扰数值外的子树内部节点的单后代交叉	48.5%
对除了可扰数值外的端点的单后代交叉	9%
对可扰数值的单后代交叉	9%
复制	10%
普通突变	1%
子程序复制	1%
子程序创建	1%
子程序删除	0.5%

第二种方法的好处是可以进行普通的交叉操作，即插入一个可扰动的数值来代替选定的其他可扰动的数值。

算术子树和可扰数值作为端点

第三种方法是算术子树中的端点都为可扰数值，这种方法综合了前两种方法，提供了一种“中等等级”的突变造成的影响。在这种情况下，树形结构可以提供一定的突变能力，同时可扰数值限制了交叉时对个体的扰动不会过大。而且第三种方法允许自由变量加入，也因此允许引入自动定义函数机制。

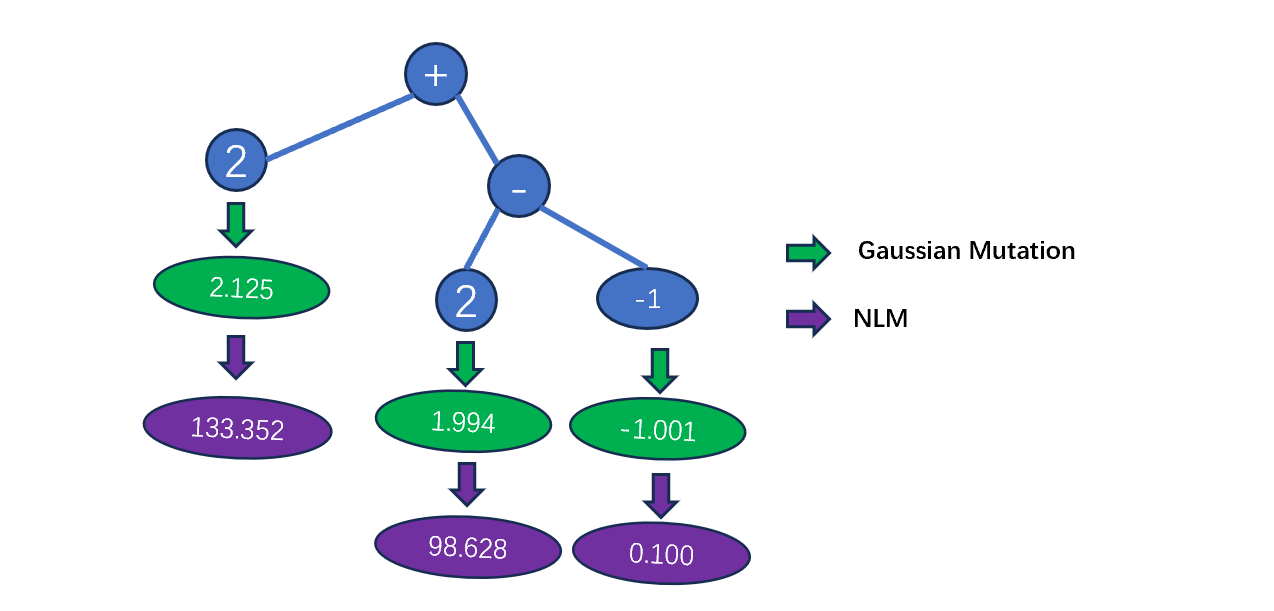
除了这三种方法外，还有GEP-GA混合架构的应用，参考^{<span class="hint--top hint--rounded" aria-label="J. Wan, H. Yin, K. Liu, C. Zhu, X. Guan and J. Yao, "A Hybrid Genetic Expression Programming and Genetic Algorithm (GEP-GA) of Auto-Modeling Electrical Equivalent Circuit for Particle Structure Measurement With Electrochemical Impedance Spectroscopy (EIS)," in IEEE Sensors Journal, vol. 23, no. 5, pp. 4344-4351, 1 March1, 2023, doi: 10.1109/JSEN.2021.3106160.">[1]}。大致是使用GEP或者GP先找到拓扑结构，然后对每个个体代表的拓扑结构使用GA找到器件的数值，然后再返回到GEP或者GP的个体中统一衡量。

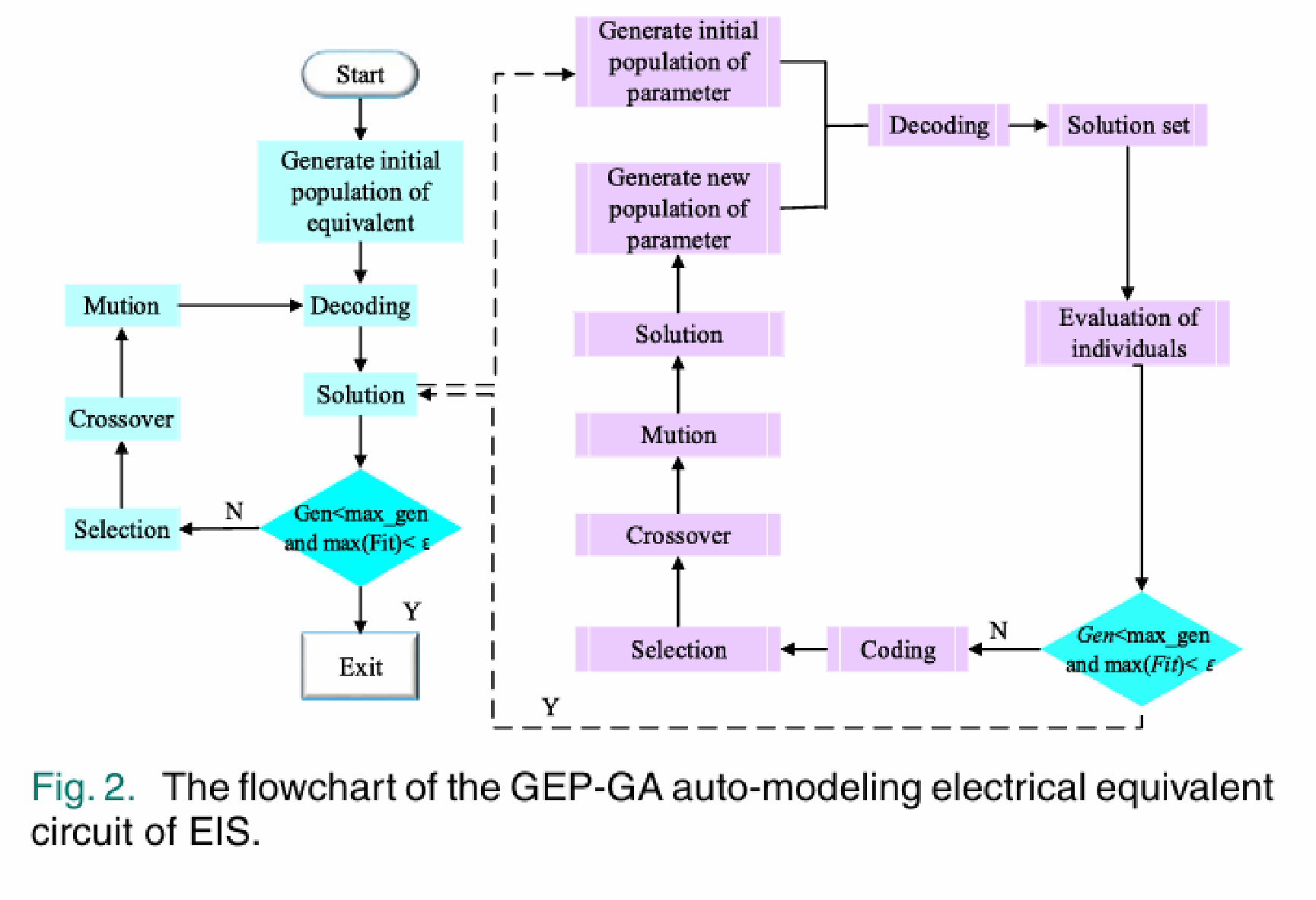
这种方法是目前的一种权宜之计，即先把拓扑结构的空间确定，再确定值的空间。但是GA的应用无法保证每个拓扑结构中器件的值的信息分布是均匀的，因此效果有限。以原教旨主义的观点，仍然是GEP/GP中值随着进化过程一同进行才能得出最佳的搜索结果。

控制器的表示方法

这一小节中讲了使用传递函数、LISP语言、程序树、Mathematica语言、连接清单、SPICE 网表表示控制器电路的方法。
这里的笔记中只介绍后面会用到的表示方法。

LISP语言和程序树

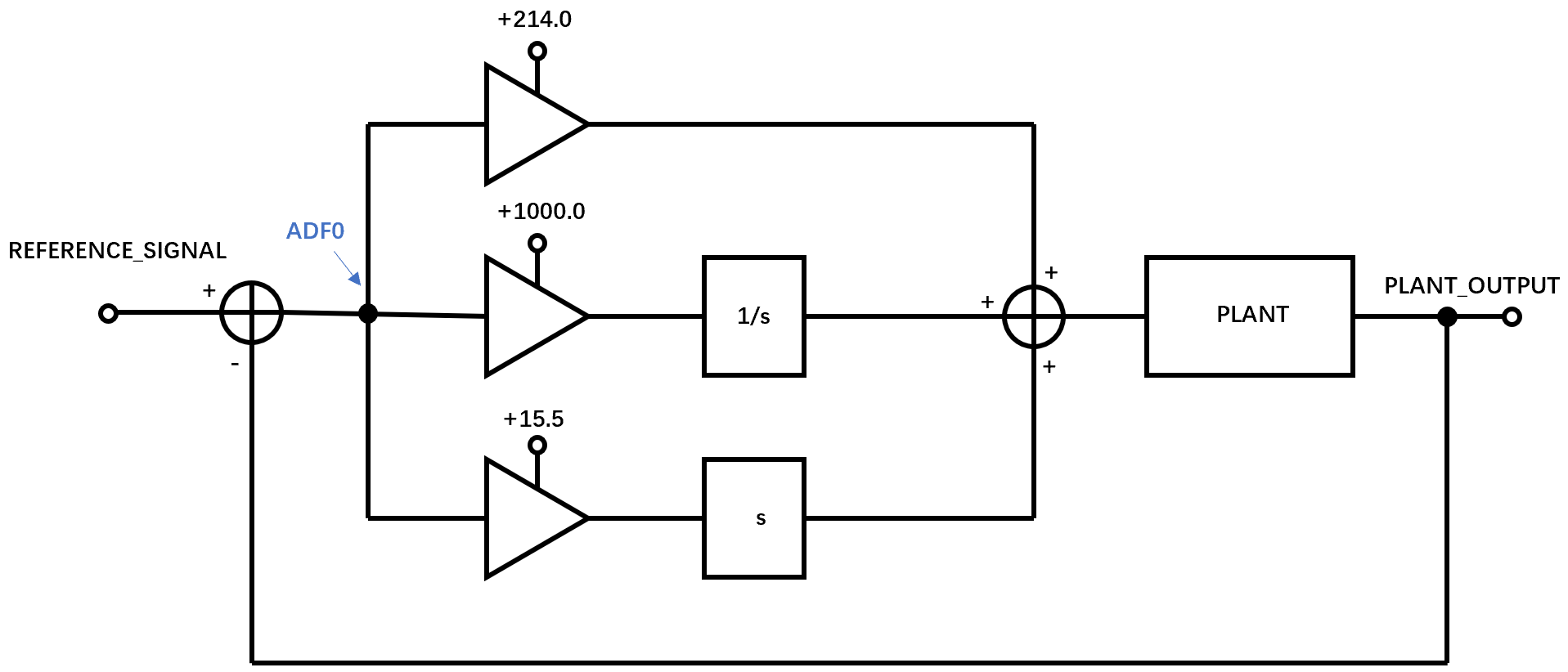
在LISP语言中一个PID控制器的例子表示上图的控制器和原型电路：

( PROGN
  ( DEFUN ADF0 ()
    ( VALUES
      (- REFERENCE_SIGNAL PLANT_OUTPUT))) ;表示并联区域信号的输入和输出
    ( VALUES
      ( +
        (GAIN 214.0 ADF0) ;P控制器
        (INTEGRATOR (GAIN 1000.0 ADF0 )) ;I控制器
        (DERIVATIVE (GAIN 15.5 ADF0 )))) ;D控制器
)

此处书中有一个印刷错误，程序的第8行应该是INTEGRATOR，第9行应该是DERIVATIVE，此处已经纠正过来了。

LISP语言采用的S-expression方法可以和程序树互转，因此上面的程序也可以表示为：

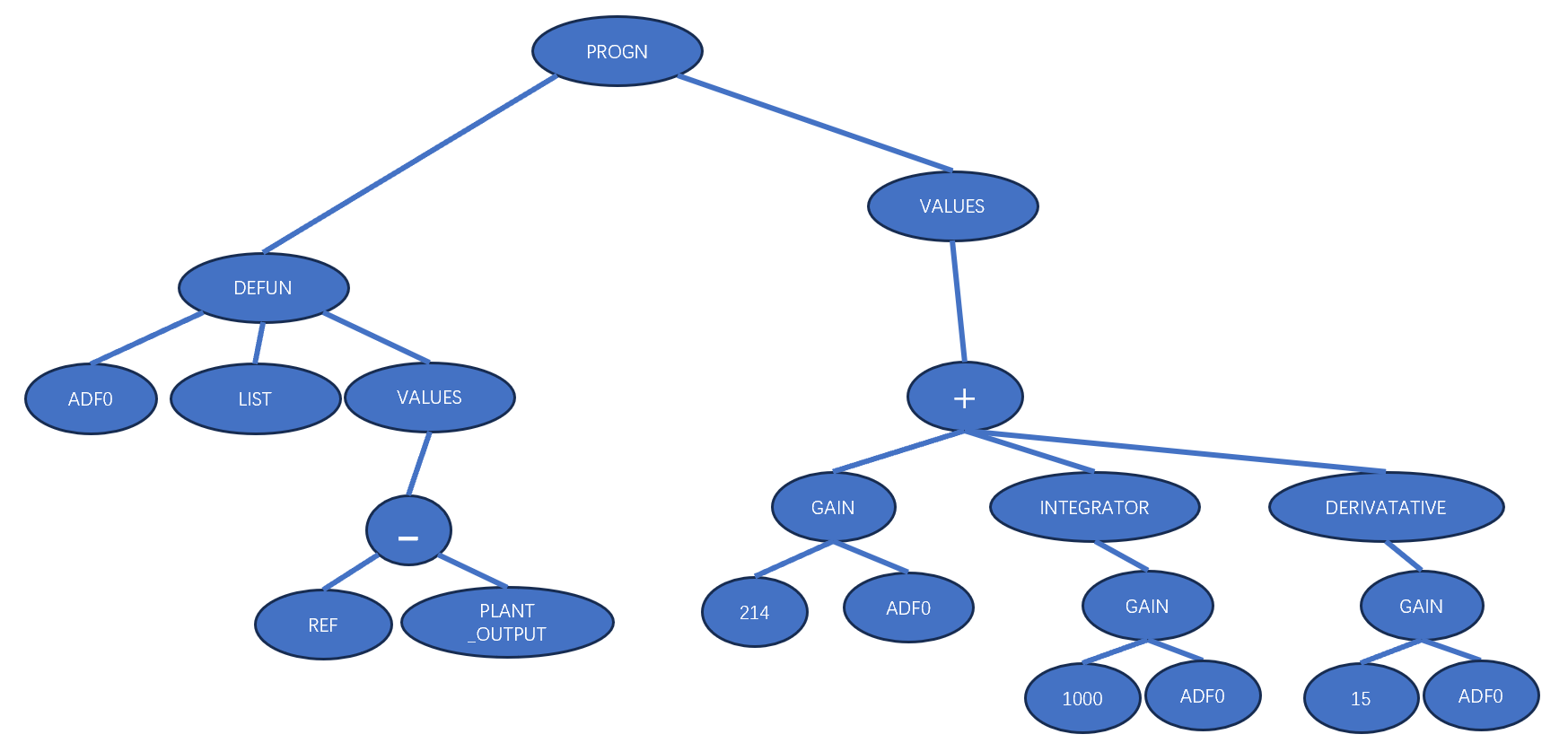
连接清单

连接清单(connection list)是一个记录电路元件之间连接关系的列表，包括元件的名称、引脚号、连接方式等信息。在电路仿真中，连接清单可以帮助用户更好地理解电路的结构和工作原理，方便用户进行电路的设计和调试。
连接清单基本结构是一行一个器件：每一行的开头为器件的输入节点，最后一个节点编号对应输出节点。然后紧随器件模块的名称和对应的声明。

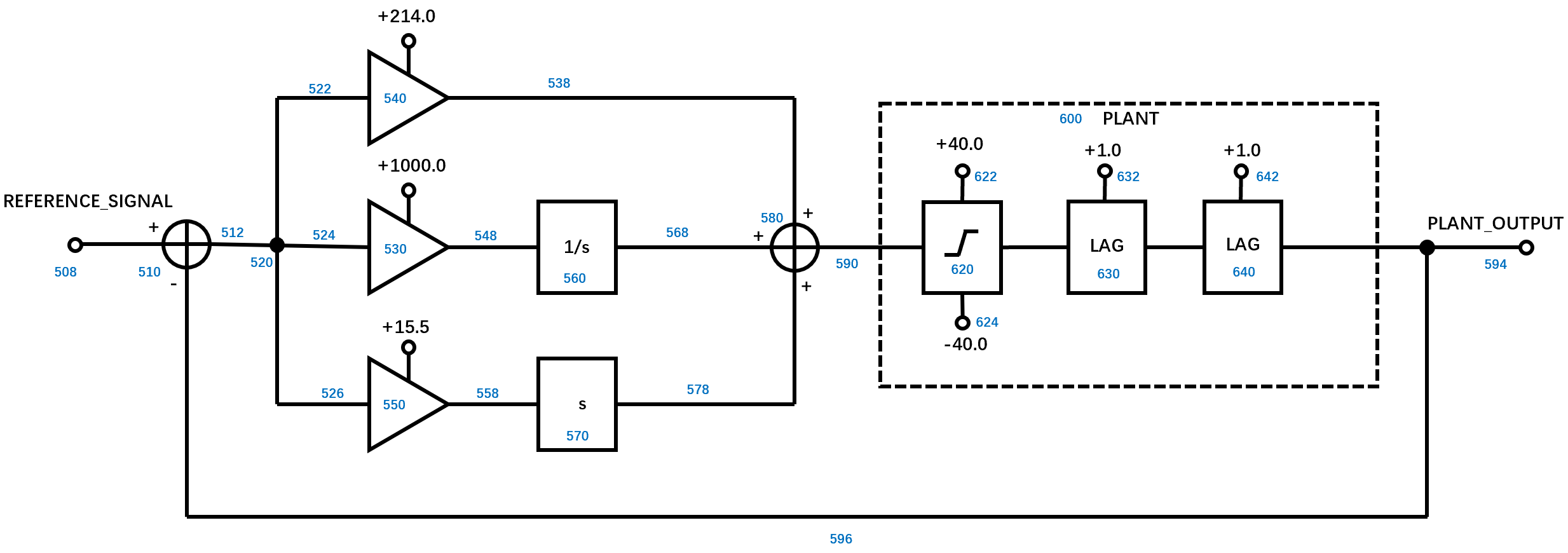
比如对于上面的电路，连接清单表示如下：

#输入   输出 模块
508 596 512 SUBTRACT
#输入输出 模块 声明
512 538 GAIN 214.0
512 548 GAIN 1000.0
548 568 INTEGRATOR
512 558 GAIN 15.5
558 578 DERIVATIVE
538 568 578 590 ADDITION
590 626 LIMITER 40.0 40.0
626 636 LAG 1.0
636 596 LAG 1.0

SPICE网表

在这个设计例子中，每一个个体最终都会被翻译为SPICE网表(SPICE netlist)然后进入SPICE仿真。SPICE网表的命令包括如下几个成分：

• 电路器件的命名
• 需要仿真的电路的网表
• 让SPICE进行何种仿真的指令
• 子电路定义
• END结束符

但是原始的SPICE仿真软件中的器件库太少，因此还需要自己对一些器件的功能和结构进行定义。

下面的SPICE指令用于构建上图的电路并且进行仿真。

.PID CONTROLLER, TWO-LAG PLANT, AND ITAE CALCULATOR
*
* THE PID CONTROLLER
* THE OUTPUT OF CONTROLLER (CONTROL VARIABLE) IS AT 590
* THE REFERENCE SIGNAL IS AT 508
* THE PLANT OUTPUT (FEEDBACK TO CONTROLLER) IS AT 596
X1 508 596 512 SUBV_SUBCKT * V(512)=V(508)-V(596)
B2 538 0   V=V(512)*214.0  * V=V(512)-GND
B3 548 0   V=V(512)*1000.0
X4 548 0   568 DII_SUBCKT  * X表示这一行用到了Subcircuit
B5 558 0   V=V(512)*15.5
X6 558 578 DIFFB_SUBCKT
X7 538 568 578 590 ADD3_SUBCKT
*
* THE TWO-LAG PLANT
* THE PLANT INPUT IS AT 590
* THE PLANT OUTPUT (FEEDBACK TO CONTROLLER) IS AT 594
X8 590 626 622 624 LIMIT_SUBCKT
X9 626 632 636 LAG_SUBCKT
X10 636 642 594 LAG_SUBCKT
V11 622 0 DC 40 * V表示供电，下同
V12 624 0 DC 40
V13 632 0 DC 1.0 * 这是LAG的供电
V14 642 0 DC 1.0
*
* 没有积分器的器件，需要自己写一个，下同
* CALCULATION OF INTEGRAL OF TIME-WEIGHTED ABSOLUTE ERROR (ITAE)
X15 508 594 508 7 ITAE_SUBCKT
* 表示V(508) - V(594)的时域积分，V(508)是参考信号，V(594)是原型输出
*
* 产生的参考信号的描述
* REFERENCE SIGNAL 508
VP16 508 0 PULSE(0.0 1 0.1 0.001 0.001 10 15) 
* 参考信号是一个持续15秒，脉宽为10秒，上升沿下降沿各0.001秒，间隔0.1秒的方波脉冲信号
*
* SPICE的仿真和画图
* COMMANDS TO SPICE FOR TRANSIENT ANALYSIS AND PLOT
.TRAN 0.08 9.6 0.0 0.04 UIC
* 以0-9.6秒，每0.08一个step进行时域分析
.PLOT TRAN V(7)
* 画出V(7)的时域图
*
* SUBCIRCUIT DEFINITION FOR SUBV
.SUBCKT SUBV 1 2 3 * 有三个输入输出端口
B1 3 0  V=V(1)–V(2) * B表示一个理想电压/电流源，VCC=3V，VDD=0V
.ENDS SUBV * 定义结束
* SUBCIRCUIT DEFINITION FOR TWO-ARGUMENT ADDV
.SUBCKT ADDV 1 2 3
B1 3 0 V=V(1)+V(2)
.ENDS ADDV
*
* SUBCIRCUIT DEFINITION FOR THREE-ARGUMENT ADD3
.SUBCKT ADD3 1 2 3 4
B1 4 0 V=V(1)+V(2)+V(3)
.ENDS ADD3
*
* SUBCIRCUIT DEFINITION FOR INVERTER
.SUBCKT INVERTER_SUBCKT 1 2
B1 2 0 V= V(1)
.ENDS INVERTER_SUBCKT
*
* SUBCIRCUIT DEFINITION FOR MULV
.SUBCKT MULV 1 2 3
B1 3 0 V=V(1)*V(2)
.ENDS MULV
*
* SUBCIRCUIT DEFINITION FOR DIVV
.SUBCKT DIVV 1 2 3
B1 3 0 V=V(1)/V(2)
.ENDS DIVV
*
* SUBCIRCUIT DEFINITION FOR ABSV
.SUBCKT ABSV 1 2
B1 2 0 V=ABS(V(1))
.ENDS ABSV
*
* SUBCIRCUIT DEFINITION FOR DIFFB (DERIVATIVE)
.SUBCKT DIFFB_SUBCKT 1 2
G1 4 0 1 0 1.0 * G表示VCCS
L1 4 0 1.0     * L表示电感
B1 2 0 V= V(4) * B表示电压源
.ENDS DIFFB_SUBCKT
*
* SUBCIRCUIT DEFINITION FOR DII
.SUBCKT DII_SUBCKT 1 2 3
G1 4 0 1 2 1.0
R1 4 0 1000MEG
C1 4 0 1.0 IC=0V
X1 4 3 INVERTER_SUBCKT
.ENDS DII_SUBCKT
*
* SUBCIRCUIT DEFINITION FOR LAG
.SUBCKT LAG_SUBCKT 1 2 3
X1 1 3 4 DII_SUBCKT
X2 4 5 3 MULV
X3 6 2 5 DIVV
V1 6 0 DC 1.0
.ENDS LAG_SUBCKT
*
* SUBCIRCUIT DEFINITION FOR LEAD
.SUBCKT LEAD_SUBCKT 1 2 3
X1 1 4 DIFFB_SUBCKT
X2 2 4 5 MULV
X3 1 5 3 ADDV
.ENDS LEAD_SUBCKT
*
.SUBCKT LAG2_SUBCKT 1 2 3 4
X1 1 4 5 DII_SUBCKT
B2 6 0 
+ V=0.5*V(5)*V(2)/V(3)
X3 6 7 4 LAG_SUBCKT
B1 7 0 V=1/(2*V(2)*V(5))
.ENDS LAG2_SUBCKT
*
* SUBCIRCUIT DEFINITION FOR LIMIT
.SUBCKT LIMIT_SUBCKT 1 2 3 4
B1 2 0
+ V=URAMP(V(1)–V(4))+V(4)-URAMP(V(1)–V(3))
.ENDS LIMIT_SUBCKT
*
* MODEL FOR SSW
.MODEL SSW SW()
*
* SUBCIRCUIT DEFINITION FOR ITAE
.SUBCKT ITAE_SUBCKT 31 32 34 33
VOSPCT 3 0 DC 0.02V
VOSPEN 11 0 DC 10V
X1 6 34 4 DIVV
V2 10 0 DC 1.0 
X3 9 12 7 MULV
S4 11 9 4 3 SSW
S5 14 13 31 0 SSW
V6 14 0 DC 1.0
X7 15 34 33 DIVV
X8 7 18 17 MULV
X9 6 12 ABSV
X10 32 31 6 SUBV
X11 13 0 18 DII_SUBCKT
X12 17 0 15 DII_SUBCKT
R13 9 10 1K
R14 0 13 1K
R15 0 33 1K
.ENDS ITAE_SUBCKT
*
* END COMMAND FOR SPICE INPUT FILE
.END

使用遗传编程的控制器设计案例

二阶滞后补偿器作为原型的设计

二阶滞后补偿器的传递函数可以写作：
\[G(s)=\frac{K}{(1+τs)^2}\] 其中\(K\)是补偿器的积分增益，\(τ\)是时间常数。
如果要对这个原型设计一个控制器，从高层次的设计表述可以是：
- 整个系统的输出信号与参考信号的误差尽可能小。
- 过冲率小于2%. - 面对不同的\(K\)和\(τ\)的变化时，控制器应该有足够的鲁棒性。在这个设计问题中，设计的基准是\(K=1,τ=1\).
- 输入信号的振幅应该限制在\([-40,40]\)之间。
- 系统可以限制高频噪声。

在这个设计中遗传编程结果将会与Dorf与Bishop两人在1998年设计的低通滤波器与PID补偿器串联的控制电路结果进行对比。结果发现遗传编程设计的电路只有对比电路上升时间的56%和设置时间的32%。并且结果优于对比目标。

准备步骤

由于加入了自动定义函数机制，在运行遗传编程前的准备步骤增加了一步决定程序树结构的操作。所有的操作列在下方：
- 决定程序架构 - 指定端点集 - 指定基函数集 - 指定适应度衡量的方式 - 选择合适的运行控制参数 - 设置终止条件和最终解的选择方案

程序架构

每一个程序树只输出一个结果，因此只有一个结果生成分支。初始化阶段的所有子树都不会有ADF，ADF将在进化过程中产生。并且设置进化过程中每个个体最多只允许拥有5个ADF。

此处作者没有对超过5个ADF之后的操作会如何（比如停止ADF打包）进行具体描述。
另外，个人认为ADF的数量对进化的影响如下：
ADF的数量越多，进化的自由度越低，基因之间的交流越少。

每个结果生成分支中只允许150个结点（函数或者端点）。每个ADF中最多只允许存在100个结点。

端点集

由于这个进化过程用到了强类型，因此需要对不同类型的分支分别讨论合适的端点集。
对于算术子树，端点集为：
\[T_{aps}=\{R\},R∈[-1,1]\]

限制范围是为了避免突变的影响过大。

对于结果生成子树，端点集都是时域信号：
\(T=\){REFERENCE_SIGNAL,CONTROLLER_OUTPUT,PLANT_OUTPUT,CONSTANT_0}

基函数集

同理，对于算术子树，基函数集为：
\[T_{aps}=\{+,-\}\] 对结果生成子树，基函数集都是对时域信号的操作：
\(T=\){GAIN,INVERTER,LEAD,LAG,LAG2,DIFFERENTIAL_INPUT_INTEGRATOR,DIFFERENTIATOR,ADD_SIGNAL,SUB_SIGNAL,ADD_3_SIGNAL,ADF0,ADF1,ADF2,ADF3,ADF4}
每个ADF的基函数集为\(T\)和已经生成的其他ADF。

适应度评估

本书当中所有的适应度评估最终都会将不同的评价尺度转化为单个适应度。控制器设计是一个多目标优化问题，这里采用的方法是将不同评价尺度的适应度使用线性组合进行综合。这个设计案例中需要达到的设计要求如下：

• 最小化ITAE
  
• 过冲率低于2%
  
• 面对不同的\(K\)和\(τ\)的变化时，控制器应该有足够的鲁棒性
  
• 限制系统使其不会出现极大的输入
• 限制整个系统的带宽

对系统输入的限制要求体现在DIFFENRENTIATION函数中使用了DIV，而DIV函数中使用了LIMITER。

整个评估的过程描述如下：每个个体的树会表达为控制器电路，然后再将这个电路接入输入信号和系统原型。需要注意的是，作者没有预先规定遗传编程设计的电路一定需要连接输入信号REFERNCE_SIGNAL和系统原型，也没有预先规定连接方式。输入信号和系统原型连不连、怎么连、连几个这些问题都交给进化过程自动判断。
然后整个系统的网表会通过作者修改的SPICE模拟器自动生成，并且加入到SPICE代码中。最后运行SPICE指令，得到仿真结果。

• 对于这个二阶补偿器原型的控制器设计，每个个体需要在8种不同环境下进行测试，这8种环境是如下设置的排列组合：

  • 参考信号的幅值为\(1mV\)或者\(1V\).
  • 积分增益\(K\)为\(1\)或者\(2\).
  • 时间常数\(τ\)为\(0.5\)或者\(1\).

  在实际设计中不希望使用零极点对消的方法改变系统性质，多选用一些\(K\)和\(τ\)的取值的目的是为了避免设计出零极点对消的控制器。
  个体代表的控制器电路会在上述8种情况下测量其ITAE、过冲率和鲁棒性。

  需要注意的是，这里的适应度是越小越好，是一种罚函数。
  对罚函数和奖励函数而言，个人还是更偏向于使用奖励函数，因为奖励函数没有上线，可以无限制突出优秀个体的表现。不过仍然需要具体问题具体分析。

  这8中情况下的子适应度表示为：
  \[∫_0^{9.6}t|e(t)|A((e(t)))Bdt\] 其中\(B\)是一个常数，用于平衡参考信号幅值不同时的误差贡献：当参考信号的幅值为\(1V\)时，\(B=1\)；当参考信号幅值为\(1mV\)时，\(B=10^6\).
  \(A\)是一个与误差\(e(t)\)有关的函数，用于放大惩罚系统响应稳定后的偏移和过冲：对所有振荡幅值低于\(2\%\)的部分\(A=1\)，对稳定后大于\(2\%\)的过冲部分\(A=10\).
  

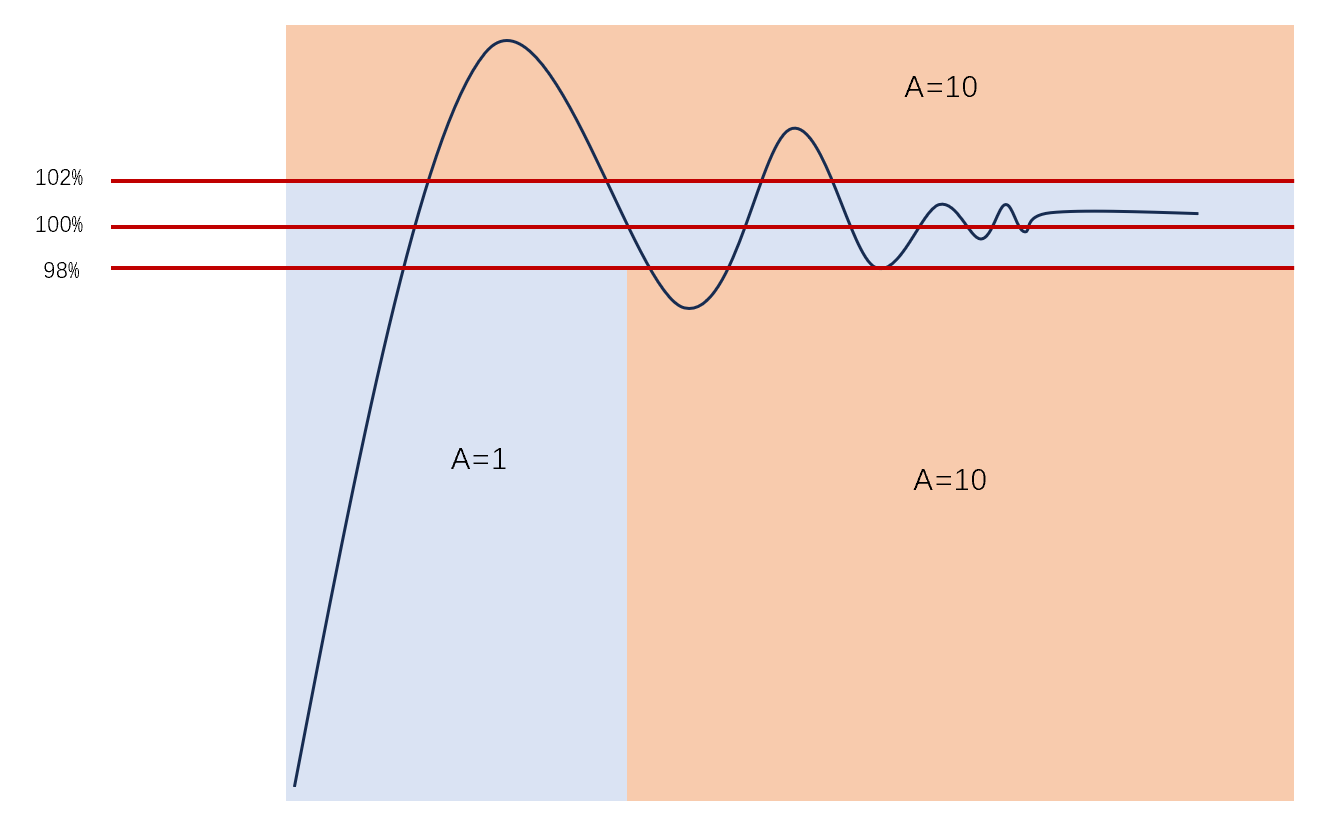
• 除此之外，为了让控制器对冲激信号不会有过度响应，在\(K=1,τ=1\)下额外测试当输入的参考信号为脉冲时的系统响应。具体做法是输入一个\(10^{-9}V\)的脉冲信号，仿真时长为120毫秒，在这121个采样点中，对原型输出的绝对值低于\(10^{-8}V\)的样本不进行惩罚。对输出的绝对值高于\(10^{-8}V\)的样本，惩罚为\(500(0.00012-t)\)。

  此处本书出现了错误，书中的描述是如此在\(t=0\)时惩罚最小，\(t=1.2\)时惩罚最大，但是根据上述函数的特征并非如此。事实上这里需要达成的目的系统对于脉冲的响应持续时间越长应该惩罚越大。

• 最后，为了保证系统的频率响应是合理的，通过频率扫描检查系统的波特图和理想系统的波特图的差异。
  设计期望的要求是整个系统(控制器和系统原型)必须对 100Hz以下的所有低频输入做出完全响应，并对 100Hz以上的输入逐渐降低响应。具体来说，1000Hz的响应不应超过 100Hz的 1/100；10000Hz的响应不应超过 10000Hz的 1/10000，以此类推。
  上面的表述换算为波特图表示如下：
  
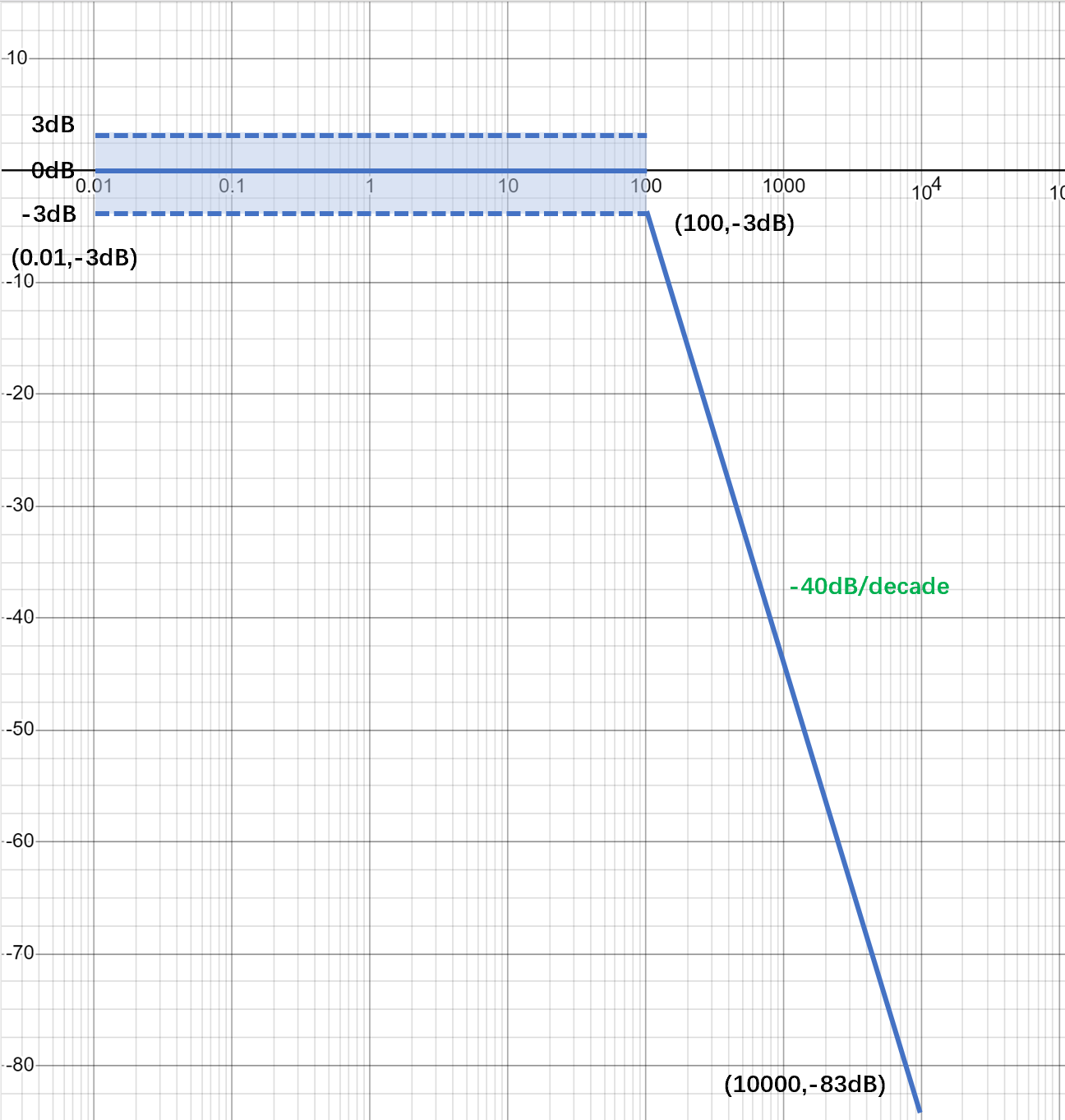
  整个适应度函数衡量的过程中会均匀抽取121个频点，对于0.01Hz到100Hz的80个频点：如果增益在0dB（误差在±3dB以内）附近，这 80 个频率值中每个频率值对适应度的贡献都是0，否则每个频点的适应度贡献都是18/121。对100Hz到10000Hz的41个频点：如果设计好的频点增益在(100,-3dB)与(10000,-83dB)连接的直线上或者直线下方，那么每个频点的适应度贡献为0，否则为18/121.

最终整个个体的适应度表示为这10个分量的和。

• 对进化过程的适应度控制如下：
  所有无法仿真的个体给予最大的适应度惩罚(\(10^8\))。
  此外还考虑了对个体复杂度的限制：如果个体的仿真运行时间超过了20秒，也给予最大惩罚。由此可以看出这个设计问题的复杂度比较高，作者强调此处复杂度高并不是遗传编程造成的，而是多目标任务本身的复杂度就比较高。

运行控制

设置初始种群大小为66000.

终止条件和最终解的选择方案

由于无法得知遗传编程在什么时候会产生一个满意的解，所以本书中的解决办法是通过设置一个非常大的停止代数，并且监控每一代最好个体的适应度来实现。当最好个体连续若干代的适应度都在满意的范围内时，停止进化。

该设计任务的人类知识参与

人类知识在这个设计任务中的参与可以分成如下几项：

• 端点集和函数集不需要过多的对系统的理解，信号的连接方式也没有预设。并且进化过程中遗传编程无从得知系统原型的结构和参考信号的样子——对于遗传编程而言，这些都是黑盒。初始化的过程并不需要由人类告诉遗传编程如何连接这些信号或者器件，也没有指定必须使用负反馈设计——一切都由进化过程决定。但是需要人类使用者告诉遗传编程有关控制器的基本组成部分。此外，这个端点集和函数集在其他控制器设计任务中也可以使用。
  此外，端点集中还有一些冗余的元素，比如这个任务中的CONSTANT_0，结果可以发现，遗传编程自身的鲁棒性允许人类使用者添加这些冗余，进化过程会自动决定它们的去留。加入冗余元素的另一个作用是可以提升端点集/函数集的泛用性，让它们也可以在别的任务中使用。此外，冗余元素的加入还有可能促使遗传编程发现那些并不符合人类直觉的结构。
  
• 适应度评估的过程中，人类做的只是将自己期望的设计标准从自然语言改写为数学语言，这个过程遗传编程自身无法完成，转换过后也屏蔽了遗传编程对专业知识的接触。
  
• 这个设计任务中使用SPICE作为评价的介质——这并不是必须的，使用SPICE只是为了自动和高效地让程序收敛到最优解，在理想状态下甚至可以由人类去实现所有个体的电路然后再测量得到适应度。SPICE本身是一个通用电路设计软件，因此其中不具备任何的有关控制器的专家知识。同时SPICE软件没有任何预设。写SPICE所加入的人类知识只是为了让SPICE程序合法。
• 控制参数的选择是和任务无关的，并且在几乎所有的任务中通用。

从此可以推断出，这个设计任务的AI比非常高。

结果分析

最初生成的第一代个体中对于设计要求基本上没有任何的感知：有些个体没有用到PLANT_OUTPUT/REFERENCE_SIGNAL，或者是使用了冗余的CONSTANT_0：

(LEAD (LAG (LAG2 (CONSTANT_0) 0.991705 0.333394)
 (+ 0.403004 0.438887)) (+ (+ 0.720283 0.273918)
 (+ 0.482394 0.075069)))

(INVERTER PLANT_OUTPUT)

(LAG2 (DIFFERENTIATOR (DIFFERENTIATOR CONTROLLER_
 OUTPUT))( (+ 0.335119 0.720933)( 0.724019 0.773270))
 0.194707)

虽然是盲选，但是第一代中最优秀的个体的适应度已经有8.26，这是因为这个个体的结构中都考虑了PLANT_OUTPUT和REFERENCE_SIGNAL，但是还没有形成负反馈结构：

(GAIN
 (DIFFERENTIATOR (DIFFERENTIAL_INPUT_INTEGRATOR
 (LAG REFERENCE_SIGNAL 0.708707) PLANT_OUTPUT))
 62.8637)

（此处为了简便表示把一个具有29个结点的算术子树浓缩为了62.8637。）

第一代会在随机初始化搜索的基础上进行进一步的搜寻，结果是当前种群中不能仿真的个体占比从60%下降到了14%。初始化搜索为后续的搜索提供了一个基线。
在第32代中，最好的个体的适应度已经达到了0.1639，遂停止搜索。这个个体的10个子适应度表现如下，整个个体表示的控制器框图如下：

相比于Dorf和Bishop设计的控制器，用遗传编程设计的控制器在各方面的表现都更优秀：

	GP的方法	Dorf和Bishop的方法
ITAE	\(19mVs^2\)	\(46mVs^2\)
干扰敏感度	\(644mV/V\)	\(5775mV/V\)
上升时间	\(296ms\)	\(465ms\)
设置时间	\(304ms\)	\(944ms\)
系统带宽 3dB	1.5Hz	1Hz

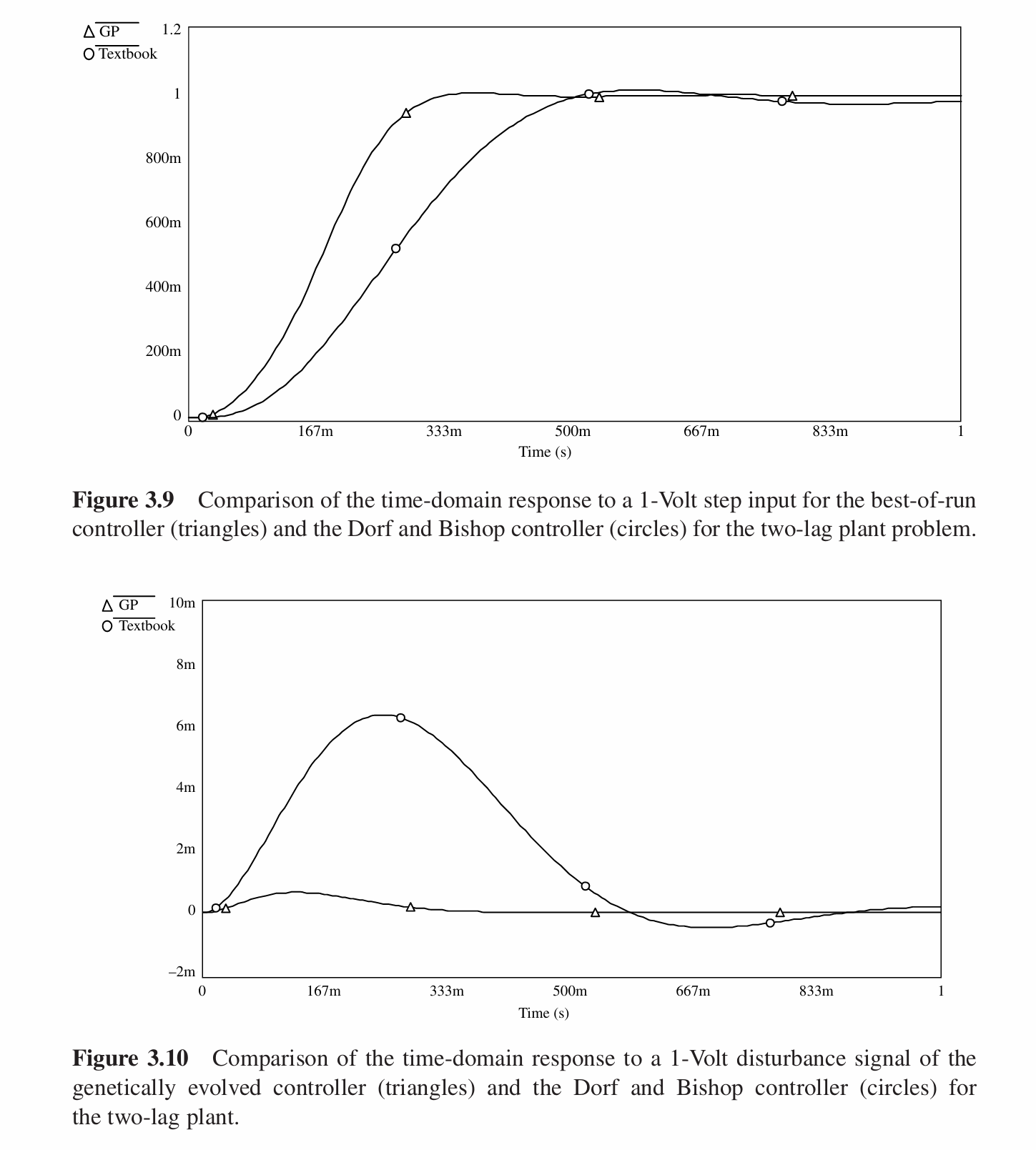
传递函数表示如下：
\[G(s)=\frac{(1+0.1262s)(1+0.2029s)}{(1+.03851s)(1+.05146s)(1+.08375)(1+.1561s)(1+.1680s)}\]

在进化的过程中，最早的初始个体中是没有ADF的，在第32代，最终种群产生了3个ADF。
ADF0的表示如下：

(ADF2)

相当于ADF0收敛到了ADF2。

ADF1的表示如下：

(LAG REFERENCE_SIGNAL (+ (+ -0.390529 
  (+ (- -0.382748 -0.853353) (- -0.558397 -0.021241))) -0.349639))

ADF1在最好的个体中没有被调用过。
ADF2中调用了ADF0，虽然存在了三个PLANT_OUTPUT（其中一个在ADF0中）但是有两个PLANT_OUTPUT相互减掉了。

出现种情况的原因是因为遗传编程找到了全局最优解的近似，但是由于精度限制始终无法进一步逼近。

(LEAD (ADD_SIGNAL (GAIN (DIFFERENTIAL_INPUT_INTEGRATOR (LEAD(LEAD PLANT_OUTPUT (+ (+ 0.331753 -0.813045) (- -0.448149 0.359068))) (+ -0.719664 -0.357372)) (ADF1)) (- (-0.773578 0.059952) -0.197462)) (CONSTANT_0) (+ -0.961429 (- (+ -0.629573 0.801392) (+ -0.495284 (- -0.130435) (- (+ -0.310777 -0.988344) (+ 0.601379 -0.649952)))))))

从上面的结果可以发现，由于较少的人类知识的投入，遗传编程甚至发现了比Dorf和Bishop解决方案更好的2D-PID架构。这足以证明在这个设计问题中遗传编程是可以比拟人类的。

三阶补偿器为原型的设计

三阶补偿器的原型系统的传递函数表示如下：
\[G(s)=\frac{K}{(1+τs)^3}\] 如果要对这个原型设计一个控制器，从高层次的设计表述可以是：

• 整个系统的输出信号与参考信号的误差尽可能小。
  
• 过冲率小于2%.
• 面对不同的\(K\)和\(τ\)的变化时，控制器应该有足够的鲁棒性。在这个设计问题中，设计的基准是\(K=1,τ=1\).
  
• 输入信号的振幅应该限制在\([-10,10]\)之间。

为了说明适应度函数的设计可以非常灵活地整合各种设计要求，此处没有对高频噪声的限制。

准备步骤

端点集和基函数集

此处采用的是直接用可扰数值来挖掘器件参数的方式，这里寻找数值的子树对应的端点集为实数范围内的可扰动化的数值。
\[T_{VSS}=\{R_p\}\] 其他子树的端点集、基函数集保持与上一个设计任务相同。

适应度评估

适应度的组成部分如下：

• 每个个体仍然在上述的8种不同环境下进行测试其ITAE、过冲率和鲁棒性。
  
• 为了让控制器对冲激信号不会有过度响应，在\(K=1,τ=1\)下额外测试当输入的参考信号为脉冲时的系统响应。
  
• 为了测量控制器的抗干扰性，在\(t=0\)时对控制器的输出信号添加一个加性噪声，再变为反馈输入。

运行控制

设置初始种群大小为66000.
其他的控制参数和上一个任务比略有不同。

结果分析

遗传编程在第31代的个体中找到最优，适应度为1.14，其系统框图表示如下：

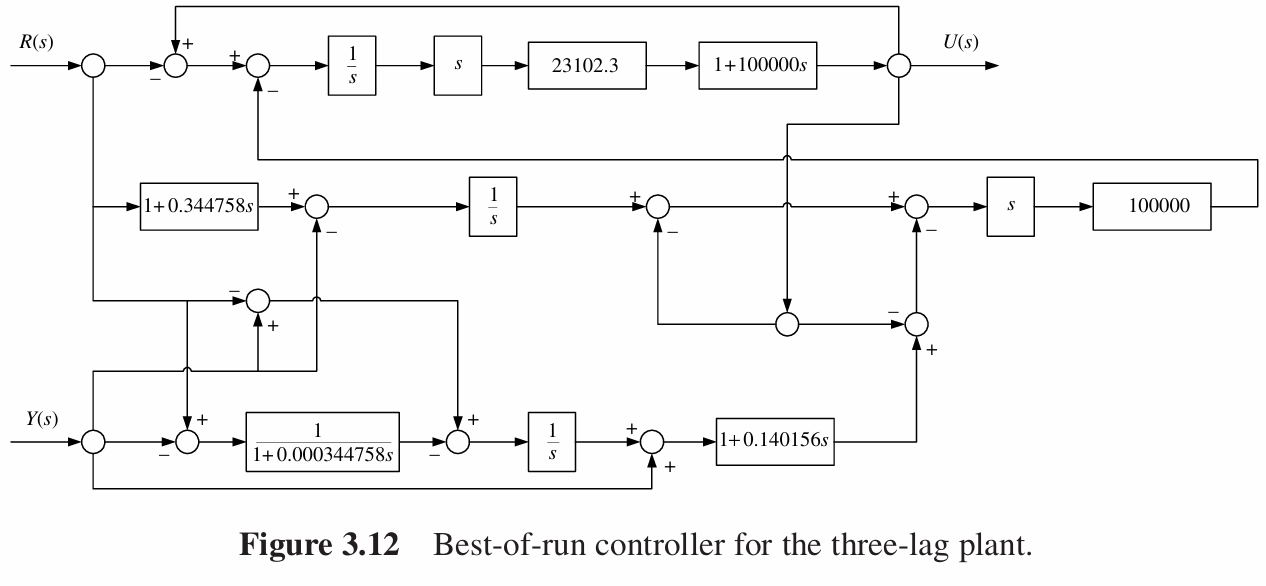
这个结果与Astrom和Hagglund设计的控制器进行对比：

	GP的方法	Astrom和Hagglund的方法
ITAE	\(0.36Vs^2\)	\(2.6Vs^2\)
干扰敏感度	\(4.3μV/V\)	\(186000μV/V\)
上升时间	\(1.25s\)	\(2.49s\)
设置时间	\(1.87s\)	\(6.46s\)
系统带宽 3dB	0.72Hz	0.248Hz

可以发现GP的方法所设计的控制器的抗干扰性要远远好于Astrom和Hagglund设计的控制器。

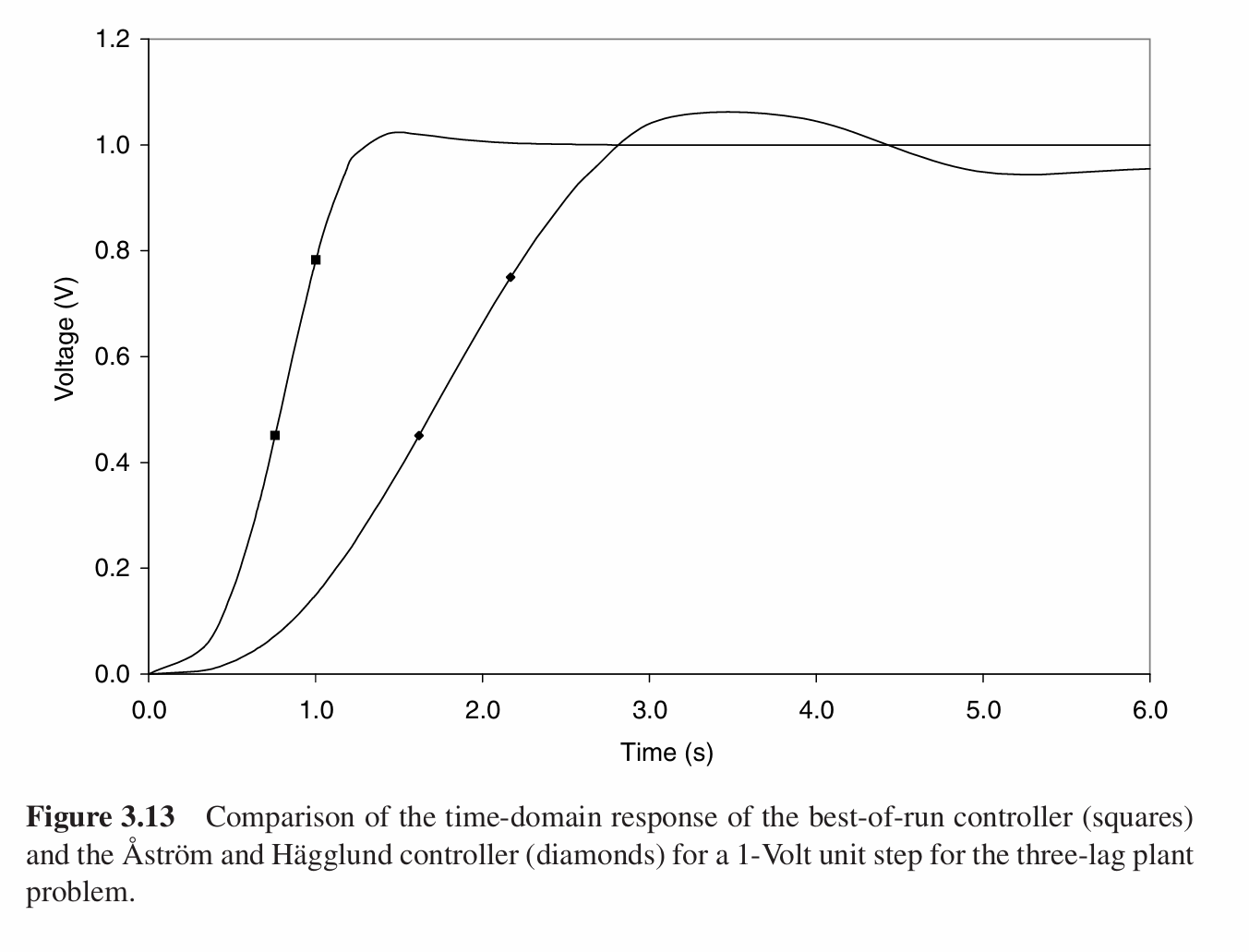
例程化分析

如果将以二阶滞后补偿器为原型的设计和以三阶滞后补偿器为原型的设计流程进行对比，可以总结出如下两个结论：

• 适应度的设计可以直接迁移到其他的控制器设计的问题上
• 即使换了寻找数值的方法，对于遗传编程的搜索过程也没有较大的影响，最终遗传编程仍然可以找到最优解

有5秒滞后的三阶补偿器为原型的设计

有5秒滞后三阶补偿器的原型系统的传递函数表示如下：
\[G(s)=\frac{K}{(1+τs)^3}e^{-5s}\]

准备步骤

准备步骤中，个体的结构和端点集的设置和三阶补偿器为原型的设计任务完全相同。

基函数集

基函数集中增加了DELAY函数，其余保持不变。

适应度评估

适应度评估包括13个子项，其中前12个子项对应在如下设置的排列组合情况的测试：

• 参考信号的幅值为\(1mV\)或者\(1V\).
• 积分增益\(K\)为\(0.9\)，\(1\)或者\(1.1\).
• 时间常数\(τ\)为\(0.5\)或者\(1\).

这12个子项的子适应度函数为：
\[\int_5^{36}(t-5)|e(t)|A(e(t))BCdt\] 新增加的系数\(C\)用于增加标准情况下偏离理想位置的惩罚，当\(τ=1\),\(K=1\)时，\(C=5\)，其余情况为\(C=1\)。

单个个体子适应度的仿真时间跨度从9.6秒拉长到了5-36秒。

控制参数

由于单个个体的适应度评估更复杂、仿真时间更长，因此初始种群的大小比之前的两个任务都小，为500000.

结果分析

遗传编程在第129代找到最佳个体，其适应度为522.605.其系统框图如下：

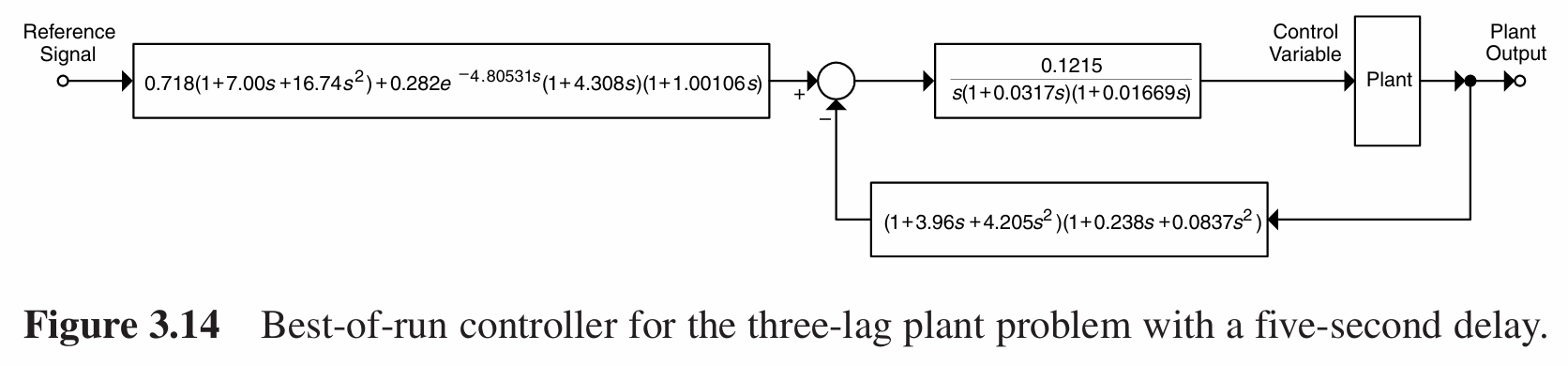
与Atrom和Hagglund所设计的控制器（下图中的方点线）的性能对比如下：

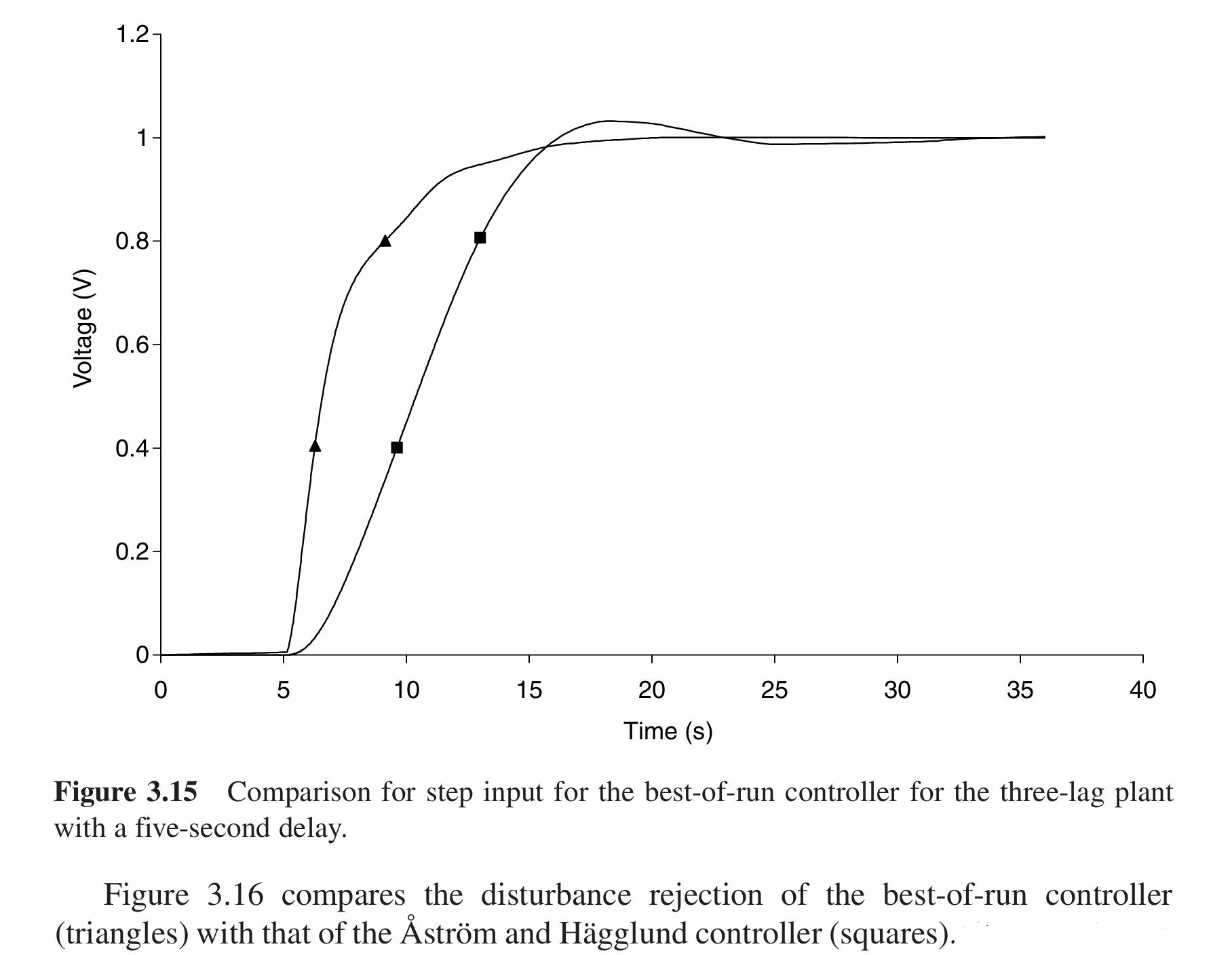
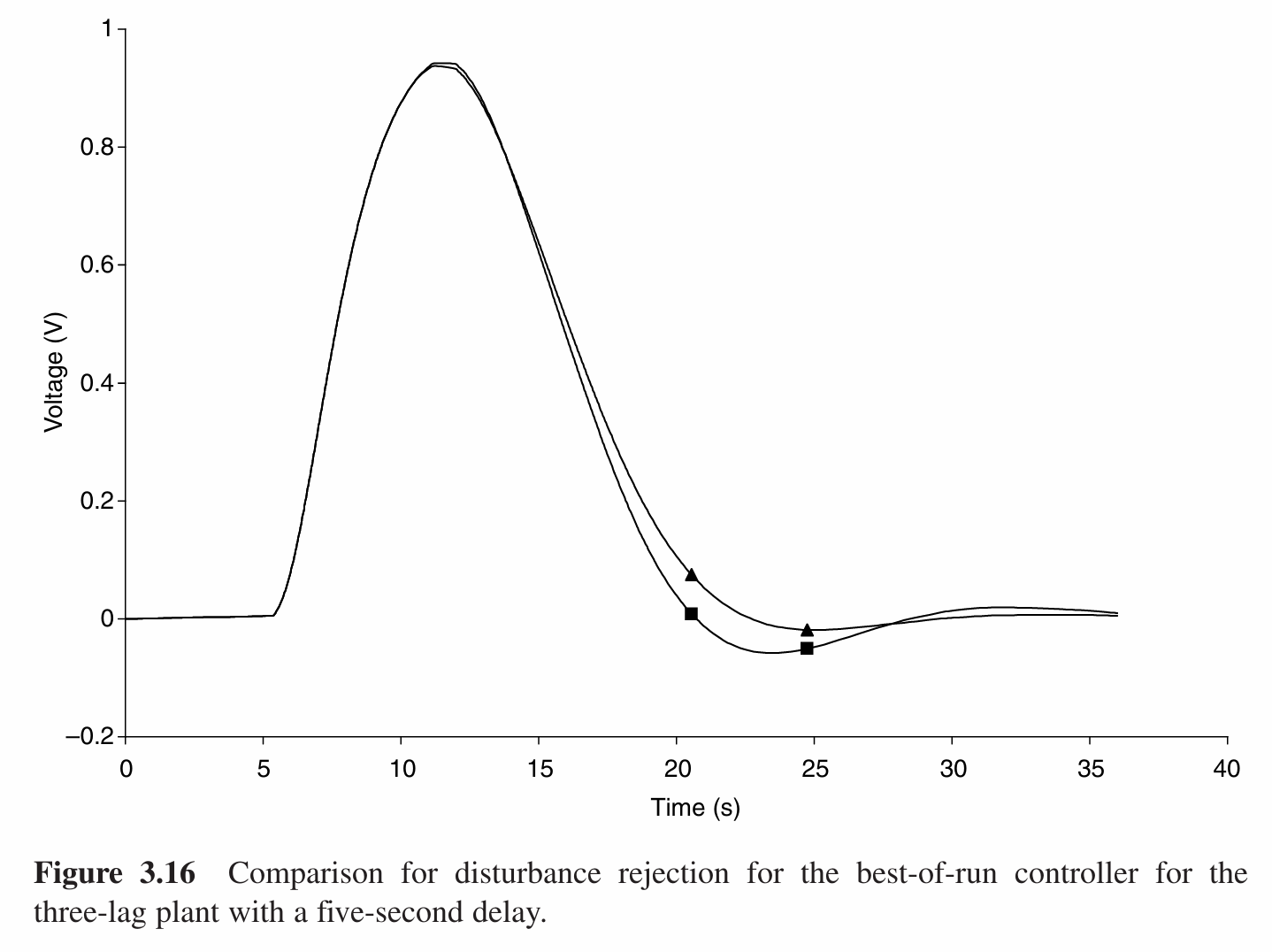
可以看出虽然遗传编程的最佳个体的适应度并不是非常高，但是最终控制器的效果仍然要优于经典方法。

非最小相位系统为原型的设计

非最小相位系统的传递函数表示如下：
\[G(s)\frac{K(1-0.5s)}{(1+τs)^2}\] 这个设计任务与之前的几个设计任务并无不同，因此在这里略过。

总结和分析

从上面的设计任务中可以看出，只需要花费一点点修改，就可以让遗传编程适用于其他的多种不同的设计任务，说明了遗传编程的可例程化程度高。并且这些设计任务中所需要的人类经验和知识非常少，但是得到的结果确实可以比拟人类的，因此可以说遗传编程的AI比非常高。

1. J. Wan, H. Yin, K. Liu, C. Zhu, X. Guan and J. Yao, "A Hybrid Genetic Expression Programming and Genetic Algorithm (GEP-GA) of Auto-Modeling Electrical Equivalent Circuit for Particle Structure Measurement With Electrochemical Impedance Spectroscopy (EIS)," in IEEE Sensors Journal, vol. 23, no. 5, pp. 4344-4351, 1 March1, 2023, doi: 10.1109/JSEN.2021.3106160. ↩︎