04. 电路的自动综合

电路的自动综合

这是对《Genetic Programming IV: Routine Human-Competitive Machine Intelligence》的笔记，本页对应第四章： Chapter 4： Automatic Synthesis of Circuitss.
这一章讲述了如何使用遗传编程完成模拟电路和混合电路的自动设计。

原书的免费公开版本在作者Koza本人的Research gate主页上：https://www.researchgate.net/publication/243776894_Genetic_Programming_IV_Routine_Human-Competitive_Machine_Intelligence
这本书也可以在Springer 购买电子版： https://link.springer.com/book/10.1007/b137549
或者在亚马逊英国购买纸质版： https://www.amazon.co.uk/Genetic-Programming-IV-Human-Competitive-Intelligence/dp/0387250670

和上一章控制器的自动综合一样，电路的自动综合也包括电路拓扑设计和器件的取值(sizing)两个方面。电路的拓扑结构(topology)包括电路中器件的个数、位置和端口连接。电路中器件的特性通常是由对应的数值进行描述的（比如：电阻、电感等等）。
有相当多的前人尝试过若干种电路的自动综合方法，但是包含模拟电路和数字电路部分的混合电路是否可以进行自动综合仍然是一个待解决的问题。其原因是虽然混合电路中模拟电路部分的占比通常比较少，但是其综合时间花费往往相比于数字电路部分要多得多。模拟电路部分的综合是混合电路综合问题的瓶颈。为了模拟设计以观察其运行特性，工程师必须开发测试平台，设定运行目标，运行模拟，必要时修改电路，并重复这一过程，直到达到设计目标。由于模拟仿真是计算密集型的，因此这一过程所需的时间比数字仿真更长"。

使用遗传编程进行电路自动综合的方法论

如果使用遗传编程来完成这个任务，使用者需要：

• 用遗传编程使用的树形结构或者S-expression表示电路
• 设置一个合理的适应度评估标准

个体的表示

在这个任务上的整体思路是保持遗传编程的运行逻辑，对评估过程进行问题的特化，在这个任务中评估过程的流程可以描述为：

• 将每个个体从树形结构翻译为电路的网表
• 通过电路仿真得到电路的特性
• 通过电路的特性计算个体的适应度

在这个评估过程中涉及到若干种个体表示方法的转换，涉及到的个体表示方法有电路图、树形结构/S-expression、以及SPICE网表。
在这个任务上，设计个体表示方式过程中遇到的最大问题是，电路是一种循环图(cyclic graph, *有起点和终点为同一个点的部分的图)，而遗传编程使用的树形结构是一种非循环图(acyclic graph)。为此，作者想到的方法是借用Kitano ^[1] 和Gruau ^[2]利用遗传编程修改神经网络的拓扑结构的方法，也采用修改的方式完成这一任务。

具体来说，一个电路被拆分为两个部分：基板电路(embryo)和测试板(test fixture)电路。其中基板电路包含至少一个可以被调整的接线(modifiable wires)。所有的修改都源于这些可以被调整的接线上。
遗传编程中的每个个体对应对这些可调接线的操作，每一个个体可能会含有插入器件、修改拓扑结构、控制合法性、进行数值运算（*用于挖掘器件的参数数值）和自动定义函数。在评估阶段，这些操作被逐个应用到基板电路上，这一过程称为“发育”(developmental process)。
紧接着，将基板电路与测试板电路连接。测试板电路会对测试板电路部分的电路性质进行测量，它的目标是将基板电路的性质以数值化的方式进行表示，以便进行适应度评估。
在本书中，我们总是特别指明测试板电路。然而，测试板电这个概念通常不会在机器学习和人工智能的文献中被明确提及，因为它们被认为是理所当然的。测试板被广泛用于用于评估由其他自动解决问题的方法（包括神经网络等等）所创建的实体的性能。 人工智能文献中经常提到的 "输入接口 "和 "输出接口 "事实上就是一个测试板。

作者在第139页举了一个在机器学习中使用测试板概念的例子：这个例子讲述了机器学习是如何根据点的空间坐标分类这个点是在双螺旋结构的哪一条支链上的。为了达成这个目的，神经网络的输出连接到了一个无法改变的外部实体(external hard-wired entity)上，这个实体用于将神经网络的输出进行二值化，得出结论这个点在哪一条支链上。这个实体就相当于此处的测试板。

在电路综合中，测试板电路通常包括信号源和源电阻、输出端和负载电阻等等。需要注意的是，测试板电路是不可以被修改的。

使用发育方法的好处如下：

• 发育方法具有保持局部性(locality)的特殊优势。由于大部分元件创建、拓扑修改和开发控制功能都是在电路的一个小局部区域内进行的，因此通过交叉操作移植的子树一般都是在局部区域内运行。发育过程与交叉操作共同作用，以保持局部性。当交叉操作将一个个体的子树替换为另一个个体的子树时，它（通常）将第一个个体创建的电路中的局部结构替换为第二个个体创建的电路中的局部结构。发育过程与突变操作在保持局部性方面的作用类似。
  
• 发育方法保留了电路的连通性(connectivity):由于基板电路本身与不可修改的测试板电路连接，因此进化过程中产生的电路很难失去连通性。
  
• 同时ADF机制允许部分有效电路得到重用。

基函数集和端点集

根据上述方法，基函数集由四部分组成：

• 拓扑结构修改函数(topology-modifying functions)：顾名思义，用于修改电路的拓扑，比如并联、串联等等。
  
• 器件插入函数(component-creating functions)：在电路中插入RLC等器件，并给它们赋予对应的数值。
  
• 发育过程控制函数(development-controlling functions)：用于控制修改电路的过程，比如no-operation函数。
  
• 数值运算函数(arithmetic-performing functions)：进行数值运算。
  
• 自动定义函数。

端点集包括如下几类：

• 常数
• 可扰数值(*通过上一章可知，可扰数值用于适当地增加进化过程的随机性)
• 自由变量
• 电路符号
  
• 零参数函数(比如：end)

在进化过程中，初始种群中的个体所有的都是合法创建的，并且运行过程中执行的所有遗传操作（即交叉、变异、繁殖和改变结构操作）都是为了保持强类型结构而设计的。 特别是，交叉操作使用点类型来确保保留强类型。因此，遗传操作所创建的个体也都是合法的。由此可得进化过程中的所有个体都应该是合法的。

In a run of genetic programming, all the individual program trees created in generation 0 of the population are syntactically valid executable programs. All the genetic operations of genetic programming (i.e., crossover, mutation, reproduction, and the architecture-altering operations) operate so as to create syntactically valid executable programs. Thus, all the individuals encountered during the run (including, in particular, the best-of-run individual) are syntactically valid executable programs.

此处所谓的“遗传操作的合法性”要么通过类保护的遗传操作和强类型实现，要么在进化过程中通过检查每一个个体实现。前者会导致进化材料无法充分在种群中交流，后者本质上是“检查-舍弃”的过程，这会浪费大量的计算资源。

不可能的设计 - 使用遗传编程综合RC电路

这一小节的目的是为了说明由于没有先验知识的加入，遗传编程可能可以找到超越人类的问题解答方式。这一小节用两个RC电路自动综合的案例来说明了这一点。

问题的背景是，Robert Pease曾经质疑过是否可以只使用电阻和电容设计出增益大于1的电路，他的结论是世界上不存在这种电路。本书的作者也曾经向若干电子工程师询问过这个问题，得到的答复都是不可能实现。但是当作者向他们展示出实际电路时，这些电子工程师通过经验分析出这个电路时可以实现增益大于1的。这件事说明由于先验知识的存在是的工程师留下了“只使用电阻和电容不可能设计出增益大于1的电路”这样的思维定式。
1956年，Phibrick ^[3] 仅仅使用电阻和电容只做了一个震荡滤波器，根据奈奎斯特定理，振荡电路的增益一定大于1，后来证明该电路的增益为1.19打破了Pease的质疑。下图展示了Phibrick的电路的结构和频率响应：

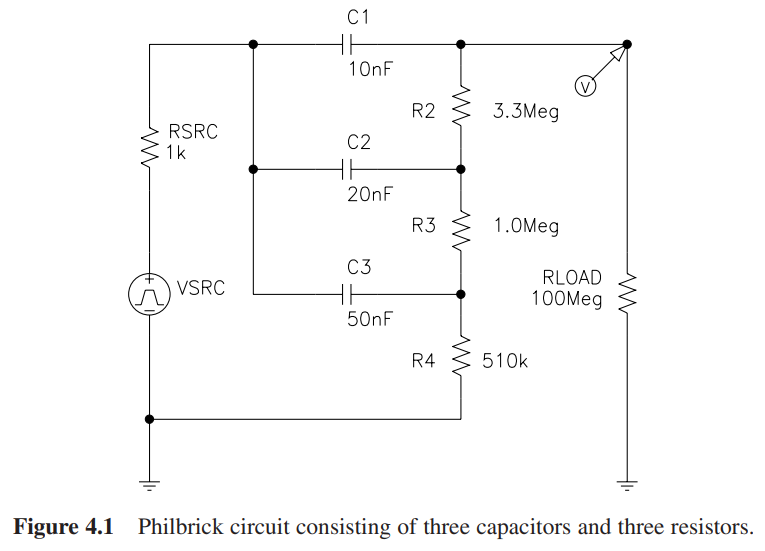
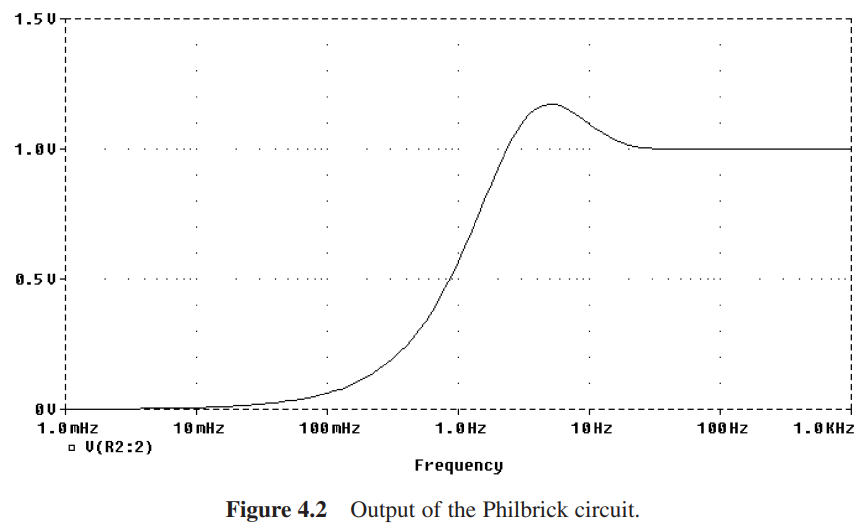
那么，问题在于是否可以让这个综合设计的过程自动化？

综合增益大于1的RC电路

Phibrick设计这个电路的用途是，在通电后的早期，该滤波器网络瞬态电压信号几乎不失真，当时当输入信号变为静态时，其输出也迅速地恢复到0电压，这种电路特性可以应用在阴极射线示波器(cathode ray oscillograph)电路中。
这个电路的另一个好处是，传统滤波器电路的组合在这个目标下的应用会出现比较大的问题：如果在非常小的失真下传输高频瞬态电压信号，那么过长的恢复时间(recovery time,*指输入开始变化到输出开始变化的时间间隔)会导致发明的实用性不高。反之如果要追求较短的恢复时间，那么传输过程的失真就很大。Phibrick的电路中几乎没有使用传统的滤波器，其传输特性使输入信号的初始高频瞬态传输基本上不失真，在经过预定的时间延迟后，无论输入信号的静态值的实际大小如何，输出电压都能相对迅速地恢复到零。

准备步骤

准备步骤包括：

1. 确定包含基板电路和测试板的初始电路结构
2. 确定电路搭建子树(circuit-constructing program tree)的结构
3. 决定基函数集和端点集
4. 确定适应度评估的方式
5. 选择合适的控制参数
6. 确定停止进化的条件和最优个体的选择方法

其中第一条是新增加的。

初始电路

初始电路分为基板电路和测试板电路，如下所示。基板电路只包括了一条可以修改的接线，而且没有参考任何已知的电路。

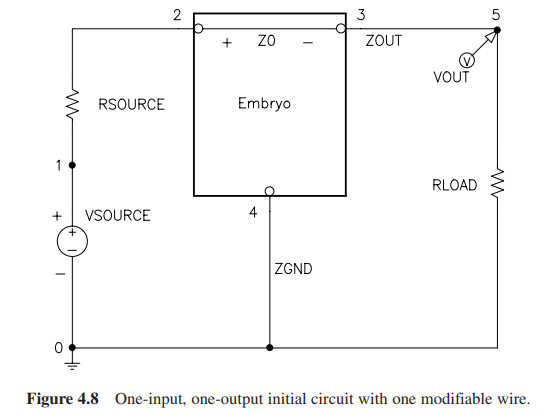
个体结构、函数集和端点集

• 个体结构
  这个问题中每个个体的结构由两种子树构成，用于修改电路拓扑结构的电路搭建子树和用于搜索插入的器件的数值的数值运算子树。
  对于电路搭建子树，由于每一条可修改的接线都需要进行输出，因此一条可修改的接线对应一个结果生成部件。在这个问题中，结构变换操作和自动定义函数都没有被使用。

我们无从得知为什么不使用结构变换操作和自动定义函数。但是Koza在1996年的论文^[4]中有使用结构变换操作和自动定义函数设计模拟电路的案例。

• 函数集
  对于数值运算子树，函数集只有加减：
  \[F_{aps}=\{+,-\}\] 对于修改电路的子树，基函数集为：
  \(F_{ccs}=\){R,C，SERIES，PARALLEL0,PARALLEL1,FLIP,NOP,PAIR_CONNECT_0,PAIR_CONNECT_1,RETAINING_THREE_GROUND0,RETAINING_THREE_GROUND1}
  其中,R和C分别对应在电路中插入一个电阻或者电容，并计算它们的数值；SERIES用于将可修改导线或可修改元件分成由可修改导线或元件组成的串联组合；PARALLEL0,PARALLEL1是两种不同的并联方式，作用是将某个点分割为由可修改导线或元件组成的并联组合；FLIP 用于翻转一个可修改导线或者元器件的极性；NOP代表不进行任何操作；PAIR_CONNECT_0,PAIR_CONNECT_1用于将两个点强行合并到一起。
  RETAINING_THREE_GROUND0,RETAINING_THREE_GROUND1用于将某个点接地。

具体的函数差异并没有在这本书以及原版论文^[5]中进行详细说明。

• 端点集
  对于数值运算子树，端点集为\([-1,1]\)的浮点型数。
  对于电路搭建子树，端点集包括包含一个零参数的发育控制函数和一个零参数的拓扑修改函数。
  \(T_{css}=\){END,SAFE_CUT}
  简言之，零参数函数END是一个发育控制函数，它使与之相关的可修改导线或者元器件变成不可修改的，从而结束特定的发育路径；零参数函数SAFE_CUT是拓扑结构修改函数，用于从发育电路中删除可修改导线或组件，同时保留电路的有效性。

适应度评估

每一个个体的适应度评估的步骤如下：

1. 将个体转换为对基板电路的操作，并将这些操作逐步应用在基板电路上。
   
2. 讲完成修改的基板电路连接到测试板上，并建立SPICE网表。网表应该同时包括基板电路和测试板电路。
   
3. 将网表输入SPICE进行仿真，并得到电路特性。
   
4. 根据电路特性计算个体的适应度。

和上一章一样，评估也不一定非得要用到SPICE软件。如果条件允许甚至可以直接搭建出电路进行仿真，或者使用FGPA、FPAA、FPTA等等方式实现。

具体而言，适应度评估了每一个个体所表示的电路与Philbrick所建立的电路的在时域和频域上的响应特性的差距：

• 在频域上，选择从1mHz到1000Hz的频率响应曲线，包括121个频点。将每一个频点的电压与Philbrick电路上对应频点的电压进行比较：对1Hz到1000Hz的61个频点，如果个体的电压值高于970mV，那么对两者的电压值差的绝对值以1的权重进行惩罚；反之如果个体的电压值低于970mV，那么对电压差的绝对值以10的权重进行惩罚。特别地，对在1mHz上的频点，对电压差加以权重为60的惩罚。最终的子适应度为各个频点上的电压差的加权和。其余的59个频点被忽略。
  
• 在时域上，Philbrick要求10ms之前可以尽可能无失真的传输高频电压，在100ms之后电路的输出电压值应当保持为0.因此，在0到10ms之间的11个采样点，如果输出的电压与1V之间的电压差的绝对值小于30mV，那么加以60的权重对电压差进行惩罚，反之则以600的权重进行惩罚；对于60ms到120ms之间的61个采样点，如果输出的电压与0V之间的电压差的绝对值小于300mV，那么加以1的权重对电压差进行惩罚，反之则以10的权重进行惩罚；

控制参数

种群的大小为660000，此外^[5]中提到单个个体的节点数上限为800.

结果分析

尽管最优秀的个体出现在第214代，适应度为663.03，但是第39代中的最优个体的适应度已经为665.55，两者提升不到0.4%。因此将第39代的最优个体视为是整个任务的最优解，其电路展示如下：

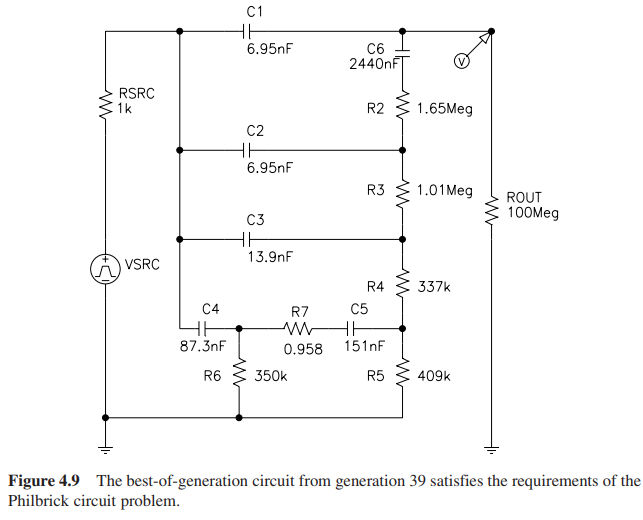
其在频率响应上的对比如下：

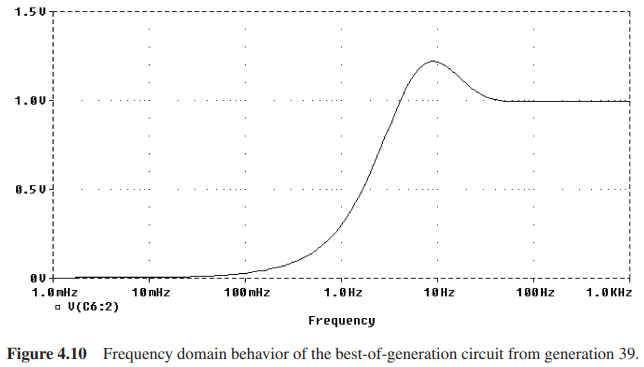
在时域上的对比如下：

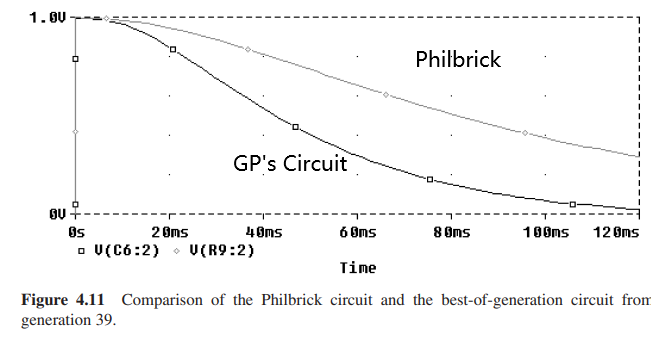
可以发现前10ms两个电路的表现基本一致，但是在10ms之后，遗传编程设计的电路的表现要好于Philbrick的设计。上述的结果满足了可比拟人类的条件。

综合增益大于2的RC电路

那么，是否存在增益大于2的RC电路呢？需要注意的是，在这个设计问题中，遗传编程不再依赖于Philbrick的电路设计，这是一个遗传编程独立解决的设计任务。

准备阶段

初始电路

初始电路和上一个问题差不多，稍微不同的是基板电路包括了两条可以修改的接线，而且没有参考任何已知的电路。

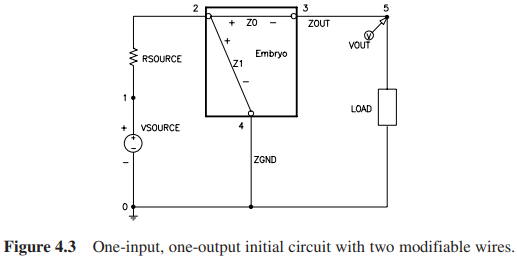
由于函数集当中有若干可以生成和拆分可修改导线的操作，因此就算最开始只有一条可以修改的导线也可以完成这个设计任务。但是这个电路相比上一个任务要复杂一些，为了降低任务的复杂度，所以增加了一条可以修改的接线。

个体结构、函数集和端点集

• 个体结构
  对于电路搭建子树，由于每一条可修改的接线都需要进行输出，因此一条可修改的接线对应一个结果生成部件。这个任务中的个体结构拥有两个结果生成部件。同样地，在这个问题中，结构变换操作和自动定义函数都没有被使用。

• 函数集
  对于数值运算子树，函数集只有加减：
  \[F_{aps}=\{+,-\}\] 对于修改电路的子树，基函数集为：
  \(F_{ccs}=\){R,C，SERIES，PARALLEL0,PARALLEL1,FLIP,NOP,PAIR_CONNECT_0,PAIR_CONNECT_1}
  其中,R和C分别对应在电路中插入一个电阻或者电容，并计算它们的数值；SERIES用于将可修改导线或可修改元件分成由可修改导线或元件组成的串联组合；PARALLEL0,PARALLEL1是两种不同的并联方式，作用是将某个点分割为由可修改导线或元件组成的并联组合；FLIP 用于翻转一个可修改导线或者元器件的极性；NOP代表不进行任何操作；PAIR_CONNECT_0,PAIR_CONNECT_1用于将两个点强行合并到一起。

这里原文当中没有RETAINING_THREE_GROUND0,RETAINING_THREE_GROUND1这两个接地函数，原因未知。

• 端点集
  和上一个任务相同。

适应度评估

适应度评估的流程和上一个任务相同，但是没有了可以用作参考的电路。由于这个问题涉及电路的频域行为，因此输出电压 VOUT 是在频域中测量的。具体来说，SPICE 受命使用不同的输出负载对每个电路进行两次交流分析。在第一次仿真中，将负载电阻的阻值设定为无穷大（即代表开路）。在第二次模拟中，LOAD 由一个 10MΩ电阻器与一个 6pF的电容并联组成（即类似示波器探头的负载）。 在每种情况下，计算适配度时只使用与 1,000 赫兹相关的电压。这个任务中个体的适应度表示如下：
\[\frac{1}{1+v_{out-infinite}}+\frac{1}{1+v_{out-oscilloscope}}\] 其中，\(v_{out-infinite}\)代表1000Hz下的开路电压，\(v_{out-oscilloscope}\)表示1000Hz下的负载电压。
另外，对于无法仿真的个体施加\(10^8\)的惩罚作为适应度。

控制参数

种群的大小为660000，此外^[5]中提到单个个体的节点数上限为800.

结果分析

在初始化阶段就已经出现了较好的个体，适应度为0.956.在第927代，最好的个体的适应度为0.622，其增益为2.24.

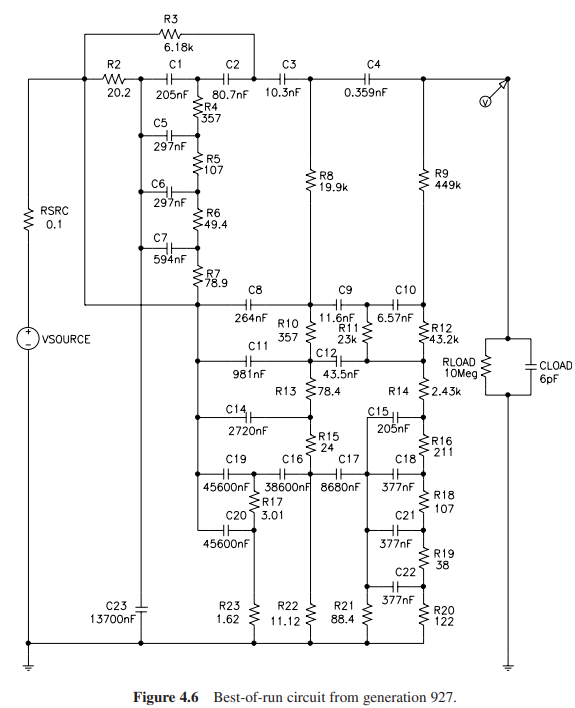
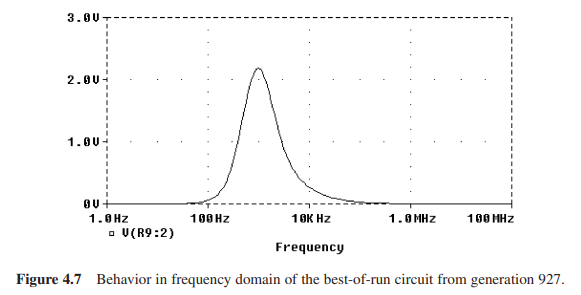
由于这两个任务都被人类认为是“不可能的设计”，因此这两个任务的“A”的程度非常高，AI比也相应地非常高。
对于例程化来说，首先，和上一章的控制器设计任务相比，这一章的设计任务并没有改变遗传编程的运作方式，因此再次说明了遗传编程的高例程化行为。

二输入NAND门的自动综合

之前的问题都是对模拟电路的综合，这个任务则是对混合电路的综合。对电路仿真来说，时域仿真的速度要比频域仿真更慢，而模拟电路的综合往往只要求进行频域分析，但是混合电路的综合往往要求进行时域和频域两方面的分析。因此，混合电路综合的难点在于时域的仿真更加耗时。与此同时，需要进行评估的适应度条件(fitness case)随着门输入个数的增加而指数型增长。
在这个设计任务中，我们要求设计出响应在100ns以内的二输入NAND门。

准备步骤

初始电路

和之前的初始电路不同的点在于，由于是双输入，因此此处的测试板电路具有两个电源和对应的源电阻。基板电路一开始拥有三个可调整的导线。

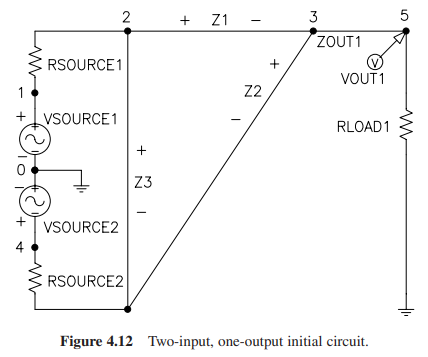
个体结构、函数集和端点集

• 个体结构
  在这个问题中，每个个体的电路搭建子树拥有三个结果生成部件。结构变换操作和自动定义函数都没有被使用。

• 函数集
  对于数值运算子树，函数集只有加减：
  \[F_{aps}=\{+,-\}\] 对于修改电路的子树，基函数集为：
  \(F_{ccs}=\){R,C，SERIES，PARALLEL0,PARALLEL1,FLIP,NOP,PAIR_CONNECT_0,PAIR_CONNECT_1,RETAINING_THREE_GROUND0,RETAINING_THREE_GROUND1,Q_DIODE_NPN,Q_DIODE_PNP,...,Q_THREE_NPN0,...,Q_THREE_NPN11, Q_THREE_PNP0,..., Q_THREE_PNP11, Q_POS5V_COLL_NPN, Q_POS5V_EMIT_PNP, Q_GND_EMIT_NPN,Q_GND_EMIT_PNP,RETAINING_THREE_POS5V_0, RETAINING_THREE_POS5V_1}
  与之前的任务的函数集不同的是增加了大量的和晶体管相关的操作：
  Q_DIODE_NPN,Q_DIODE_PNP各自对应插入一个无连接的NPN晶体管或者PNP三极管； Q_POS5V_COLL_NPN, Q_POS5V_EMIT_PNP各自对应插入一个向NPN的集电极或者向PNP的发射极输入5V的供电的三极管；
  Q_GND_EMIT_NPN,Q_GND_EMIT_PNP各自对应插入一个对NPN三极管或者PNP三极管的发射极接地的三极管；
  RETAINING_THREE_POS5V_0, RETAINING_THREE_POS5V_1是两种不同的将某个点接入5V供电的方式。

此处相当于把三极管所有可能的连接方式提前用端点的方式表现出来了。

此处为了避免仿真错误，所有需要连接电源的器件的电源都是独立的。

端点集和之前相同。

适应度评估

这个电路设计中用0V表示0，5V表示1。
评估过程如下：向个体的输入端输入从00到11的所有波形，然后比对个体的输出波形和2NAND门的理想输入波形的差距： 如果所需的数字信号为 1，而实际电压电压在\([4.7,5.3]V\)以内，或者预期数字信号为0，而实际电压在\([-0.4, 0.4]\)V以内，则与预期输出电压（5V或0V）的偏差绝对值按系数 1.0 加权。

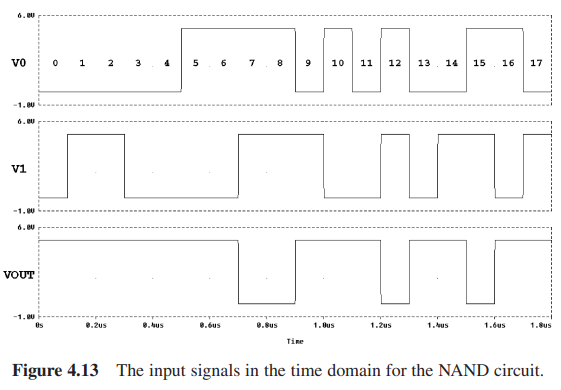
控制参数

由于消耗的计算资源更多，因此种群大小的设置比之前更少，大小为132000.

结果分析

遗传编程在第17代就得出了最好的个体，其适应度为7.85.

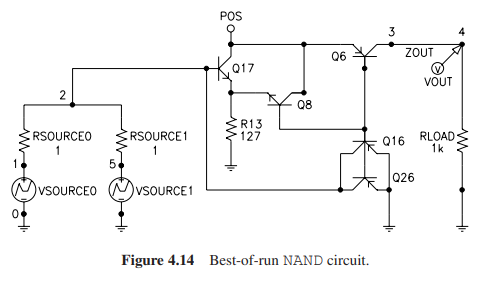
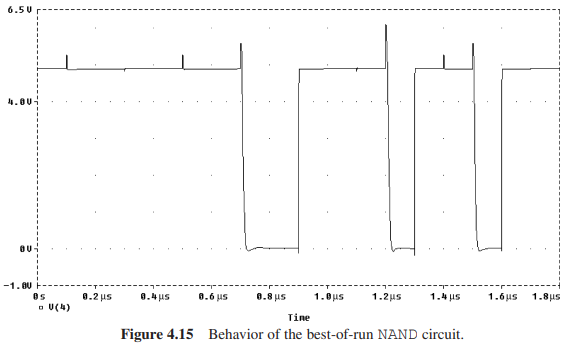
可以发现电路产生的波形中有许多毛刺，这个毛刺出现的原因和解决办法在^[6]中提到。

两个指令集的ALU的自动综合

准备步骤

这个设计任务是使用遗传编程创建一个具有NAND和NOR两条指令的ALU。其初始电路如下：

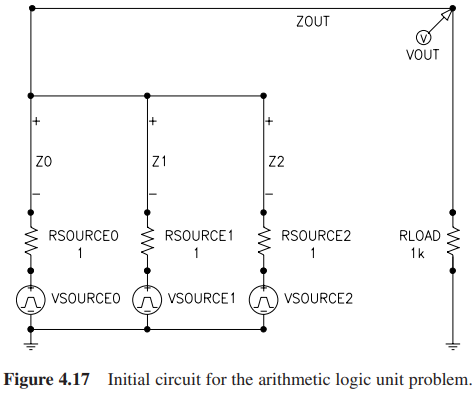
其中第三个输入VSOURCE2用于选择ALU执行的指令是NAND还是NOR。
这个任务用到的端点集和函数集、控制参数和上个任务完全相同。
适应度衡量的基本思路也是输入从000到111的所有波形，检查个体的输出波形与理想波形的差距。

结果分析

遗传编程在第33代找到最优个体，其适应度为215.6：

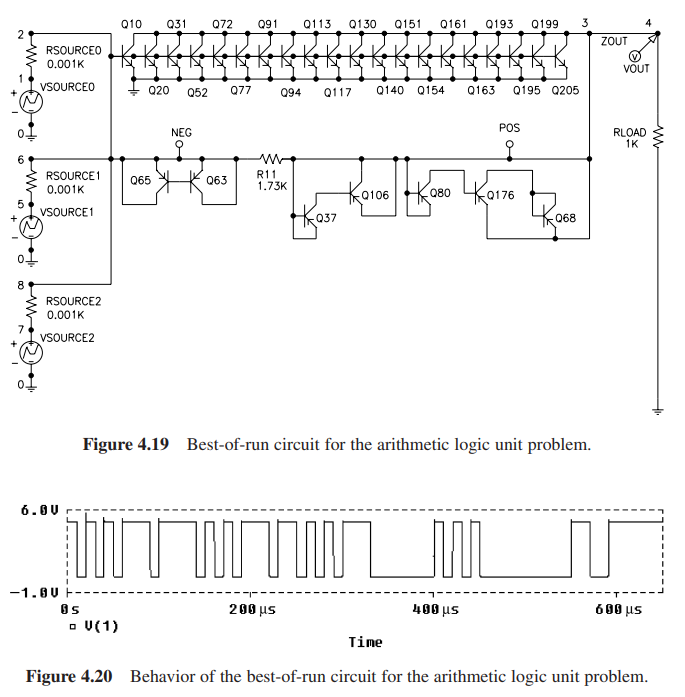
这个问题的准备步骤与以往模拟电路合成问题的准备步骤基本相同，只是本问题的目标不同（因此适应度也不同）。从以前的模拟电路综合问题过渡到现在的问题是例程化的。
遗传编程对这一问题产生的解决方案具有中等程度的 "A"。这个问题的准备步骤包含了少量的 "I"。因此，遗传编程产生的解决方案的人工智能比率为中等偏上。

平方根电路的自动综合

用模拟电路执行数学运算的电路称为运算电路(computational circuit)。之前已经有很多使用遗传编程设计计算电路的例子，但是计受到算资源条件的限制，这些工作在个体仿真阶段使用的都是DC扫描。DC扫描虽然简单，但是以此产生的电路并不能稳定地表现计算电路的功能。

准备步骤

初始电路如下：

其端点集与之前RC电路设计中使用的端点集相同。函数集增加了一个用于添加电感并赋值的函数L。
在适应度评估阶段，需要评估的情况有四种，输入信号分别为斜坡信号、三角信号、阶跃信号和方波信号时的电路输出情况。

对于适应度评估而言，作者发现如果直接使用输出的理想值减去真实值的绝对值的采样加权和(*由于遗传编程只会衡量这些采样点的值是否和理想值对齐)，在没有采样的地方会出现尖刺信号(glitches)（比如NAND设计的最后结果）。进一步地，作者发现尖刺信号是由于输入信号的变化与输出信号变化的时延造成的^[6]，因此作者在适应度设计时重点惩罚了在输入信号变化时个体实际的输出和理想输出的微小差异。
因此，具体来说，作者只考虑与 SPICE 内部创建的信号突变点相对应的时间差。因此，平方根计算电路的适配度量是 SPICE 每个突变点处 VOUT 的实际输出电压与期望输出电压之差的绝对值之和。

结果分析

最好的个体出现在第66代，其适应度为6.26989. 它可以几乎完美的实现对这四种波形的平方根输出。

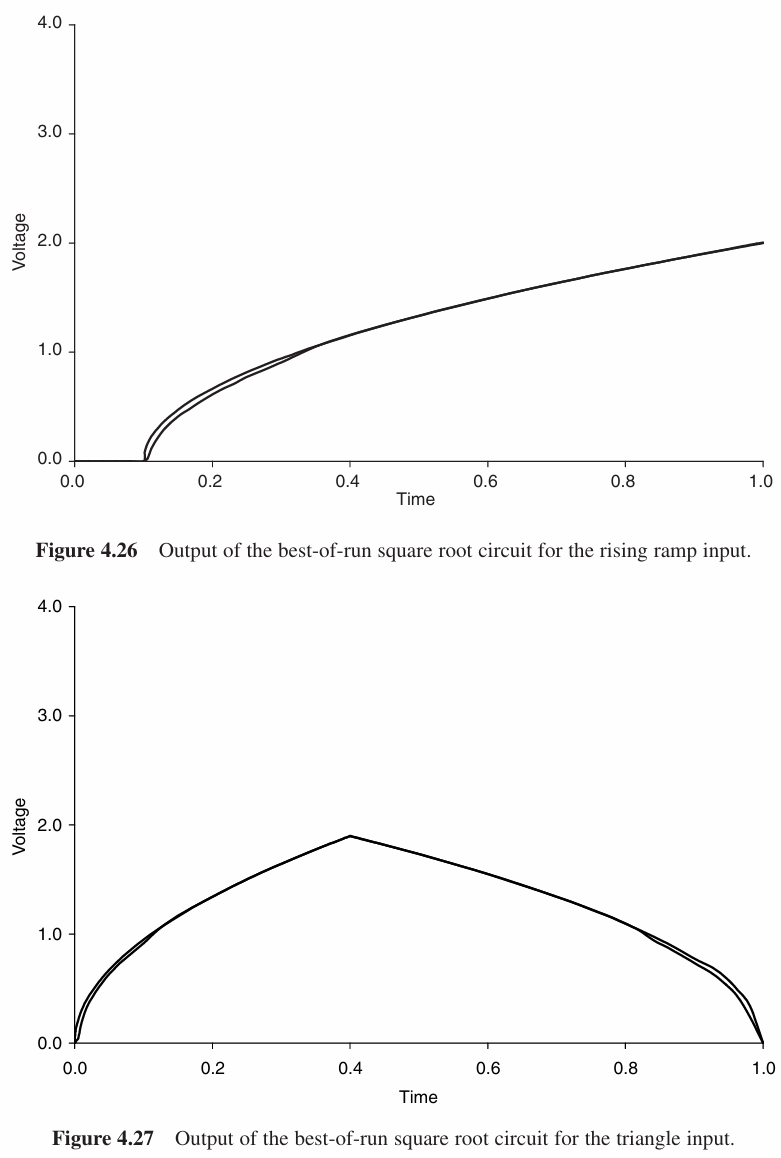
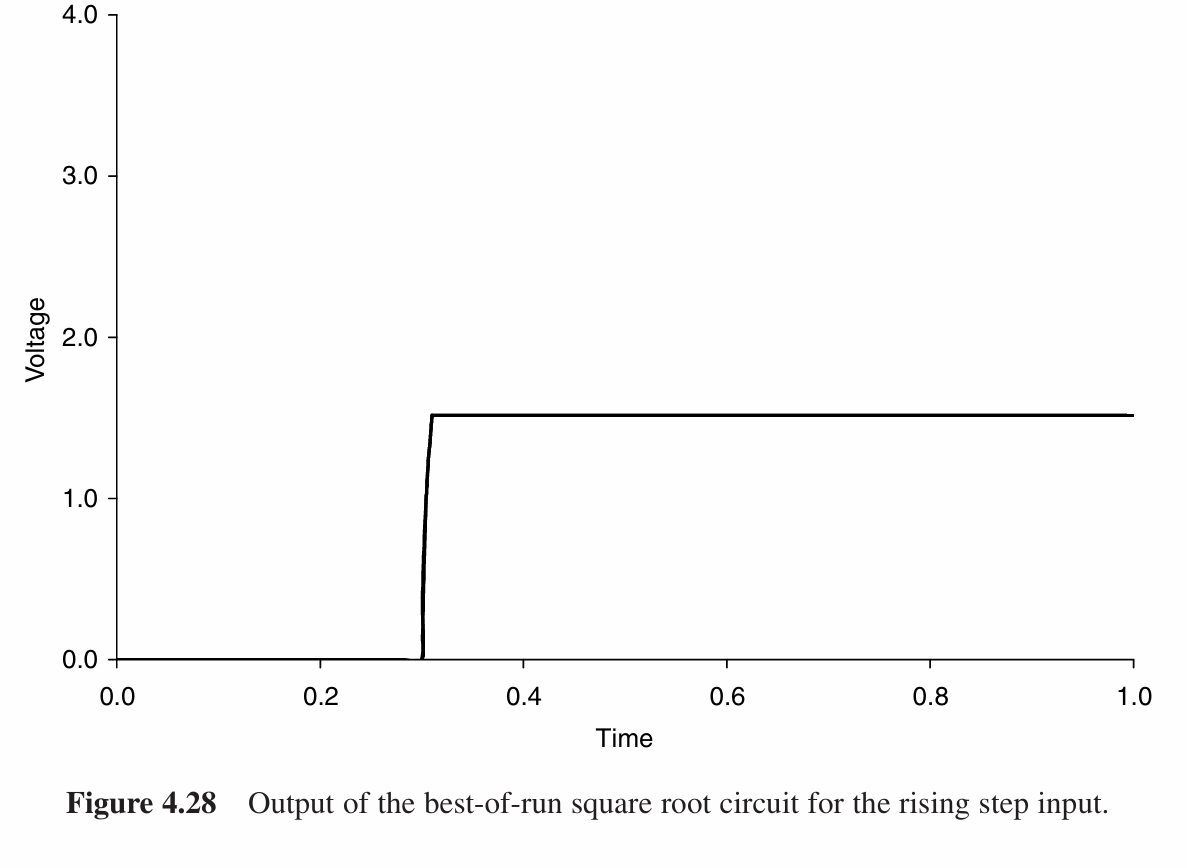
但是，在如上的任务中作者意识到，本书中通过基因创造的电路并不具备人们对所讨论的商业版电路的所有合理要求。商业电路的要求远远超出了本书中的适配措施。
此外，本书中描述的所有电路都是在仿真中验证的，而不是通过实际搭建来验证的。而且，SPICE的仿真是在由分立元件组成的电路上运行的。此外，在制造集成电路时（尤其是在高频工作时），有必要考虑硅芯片上元件的实际物理位置和芯片上导线的实际布线所产生的寄生效应和时序效应。在设计实际电路时，还必须考虑制造上的公差等等。
此外，尽管总体上很好，SPICE中使用的现有器件模型通常是在假设元件将在日常状态下工作的基础上制作的。这些模型并不一定能准确地代表所有可想象的工作状态，尤其是进化过程中可能设计出的工作状态。因此，本书中一些基因进化电路中的某些元件有可能在其模型不能代表其实际行为的情况下工作。

没有测试板的电路自动综合

在本节中，作者将演示在没有测试板中内置源电阻器和内置负载电阻的情况下，运行遗传编程可以解决电路综合问题。测试板本身是一种人类知识(I)和自动运算量(A)之间的权衡，取消测试板就需要增加计算机时间成本。
这一小节中将使用一个自动综合的低通滤波器例子来说明上述观点。
这个任务的设计目标是为了设计一个通带1000Hz，截止频率为2000Hz，衰减低于1000的低通滤波器。同时，这个低通滤波器在通带的波纹的电平应在\([970,1030]mV\)以内，止带的点平应该在\([0,1]mV\)以内。

准备步骤

由于没有测试板，但是还是需要让基板连接电路的输入、输出端和接地，以便测试出基板的电学性质，但是这并不影响遗传编程在没有任何先验结构的支撑下对基板电路进行修改的过程。

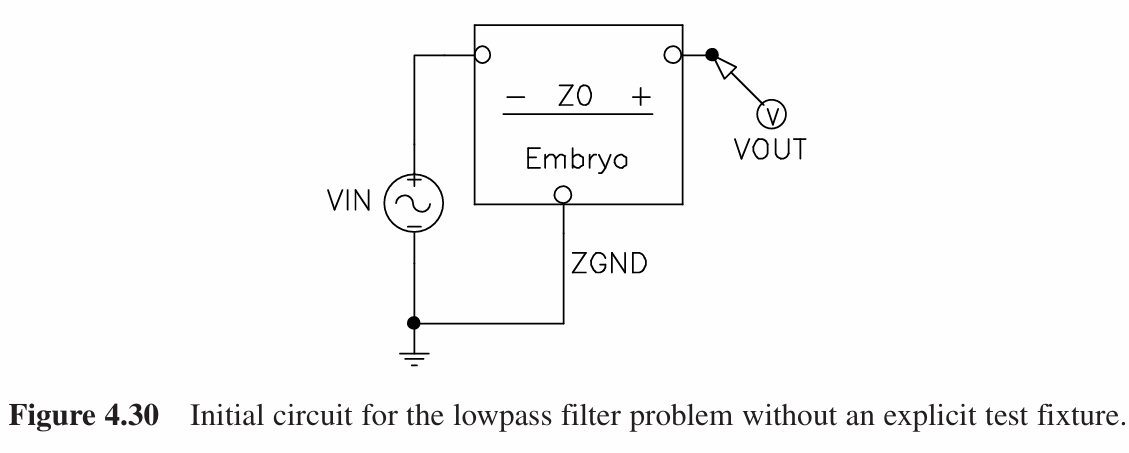
由于并没有确定基板的连接方式，所以有些进化得出的连接操作可能会在SPICE仿真中出现问题，为了避免这种情况，作者采取了如下两种方法：

• 首先是对悬垂线(dangling wire)的处理。SPICE仿真中不允许电路中存在悬垂线。因此，在这个任务中在仿真之前将电路中所有的悬垂线末端添加一个1GΩ的电阻并接地。由于这个电阻值很高，因此添加的这些电阻对电路行为没有明显影响。但是，添加这些无功能电阻器可以使 SPICE 对电路进行仿真。
  这些非常大的电阻相当于断路，不具备任何功能，所以不应将这些添加的高阻值电阻与缺失的源电阻或负载电阻（它们必须具有非极端阻值才能执行所需的功能）相混淆。

• 为了避免短路，在VIN后面增加了一个1pΩ的电阻来避免由于短路错误导致SPICE无法仿真。和上一个方法一样，这些非常小的电阻相当于导线，也不具备任何的实际功能，但是可以让SPICE能够顺利仿真。

函数集和端点集

函数集需要考虑电路的连接，于是电路搭建子树的基函数集新增加了INPUT_0这个函数，表示将一个点接入端口0。同理也可以加入INPUT_1，INPUT_2等等函数让电路的某个点接入不同的输出信号；表示输出端连接的OUTPUT_0函数亦是如此。
函数集表示如下：
\(F_{ccs}=\){TWO_LEAD,SERIES,PARALLEL_NEW,NODE,TWO_GROUND,THREE_GROUND,INPUT_0,OUTPUT_0}

其中TWO_LEAD函数将在第 10.1.4 节中介绍，该函数提供了一种在发育电路中插入双引线元件（如电阻器、电容器和电感器）的方法;
两个GROUND函数分别提供了两种不同的接地方式：使用TWO_GROUND接地后会产生两个新的可调整的导线；使用THREE_GROUND接地后会产生三个新的可调整的导线。

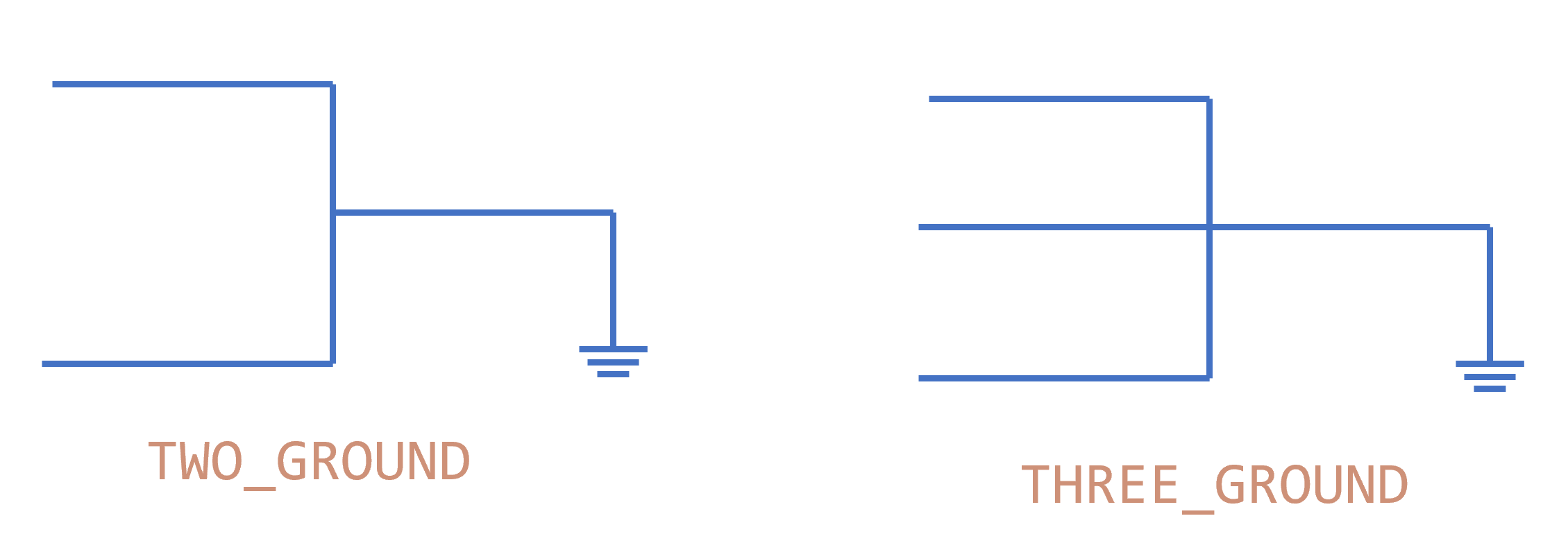
对于端点集，PARALLEL_NEW函数的端点集和其他函数不同：
\(T_{parallel}=\){UP_OR_LEFT, DOWN_OR_RIGHT}
其他函数的端点集和之前的任务都相同：
对于数值运算子树，端点集为\([-1,1]\)的浮点型数。
对于电路搭建子树，端点集包括包含一个零参数的发育控制函数和一个零参数的拓扑修改函数。
\(T_{css}=\){END,SAFE_CUT}

适应度评估

对于1Hz到1000000Hz的101个频点，适应度是所有频点的电平与理想电路频率响应上对应频点的电平值的差的绝对值的加权和：
\[F(t)=\sum_{i=0}^{100}w_i|\hat{f}_i-f_i|\] 其中\(w_i\)是权重；\(\hat{f}_i\)是理想的频率电平；\(f_i\)是个体在\(i\)出的频率响应。

权重的赋予方式是：对于1Hz到1000Hz的61个频点：如果该区间的电压等于理想值 1 伏，则偏差为 0.0。如果电压在 \([970,1030]mV\)之间，则偏离 1 伏特的绝对值按系数 1.0 加权。否则，偏离 1 伏特电压的绝对值按系数 10.0 加权; 对于2000Hz到1000000Hz的35个频点：如果该区间的电压等于理想值 0V，则偏差为 0.0。如果电压在 \([0,1]mV\)之间，则偏离 1 伏特的绝对值按系数 1.0 加权。否则，偏离 1 伏特电压的绝对值按系数 10.0 加权;
对于1000Hz到2000Hz的频点，由于设计中不关心，权重始终为0.

控制参数

种群大小为1000000. （*需要足够大才能找到目标解）

结果分析

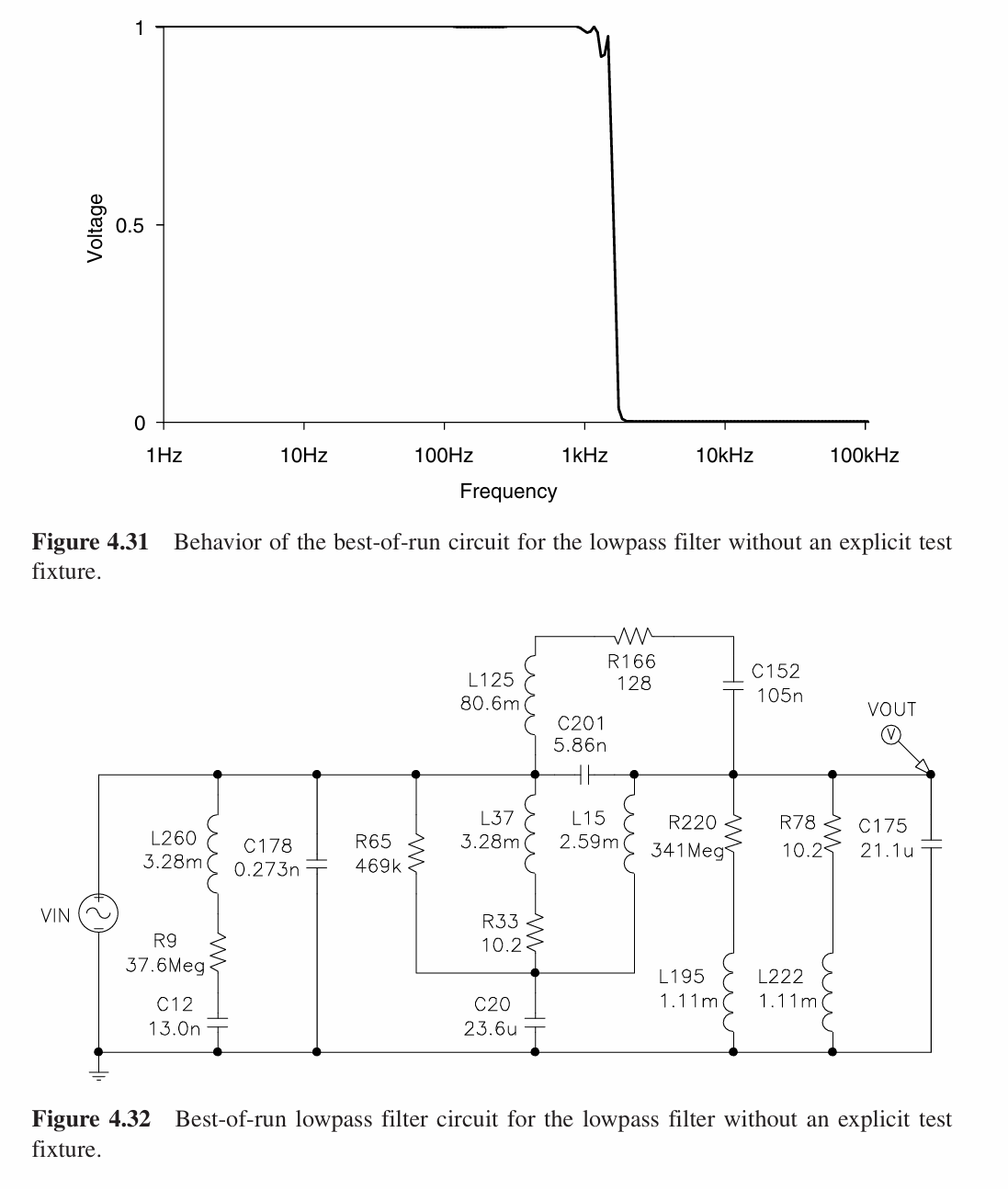
第211代中出现最佳个体，其电路和频率响应如下：

然而，事实上在第211代一次运行需要处理 212,000,000 个个体，运行耗费了 9 个小时的计算时间。这一事实有力地表明，不提供计算资源会大大增加成本。不提供测试板会大大增加计算资源成本。

1. H. Kitano, Designing Neural Networks Using Genetic Algorithms with Graph Generation System, Complex Systems, 1990. ↩︎
2. Gruau, Frédéric. (1994). Automatic Definition of Modular Neural Networks. Adaptive Behavior - ADAPT BEHAV. 3. 151-183. 10.1177/105971239400300202. ↩︎
3. George A. Philbrick,. Dover, Mass., Delayed-Recovery Electric Filter Network, US Patent: 226963, 1951. ↩︎
4. Koza, John R., Forrest H. Bennett, David Andre and Martin A. Keane. “Reuse, Parameterized Reuse, and Hierarchical Reuse of Substructures in Evolving Electrical Circuits Using Genetic Programming.” International Conference on Evolvable Systems (1996). ↩︎
5. John R. Koza et al, Searching for the Impossible using Genetic Programming, 1999. ↩︎
6. Bennett, Forrest H., John R. Koza, Martin A. Keane, Jessen Yu, William Mydlowec and Oscar Stiffelman. “Evolution by Means of Genetic Programming of Analog Circuits that Perform Digital Functions.” Annual Conference on Genetic and Evolutionary Computation (1999). ↩︎