强类型遗传编程

D. J. Montana, "Strongly Typed Genetic Programming," in Evolutionary Computation, vol. 3, no. 2, pp. 199-230, June 1995, doi: 10.1162/evco.1995.3.2.199.

强类型遗传编程(Strongly Typed Genetic Programming, STGP)是一种改进的遗传编程算法。它对遗传编程的改进有两点：

• STGP中对函数的声明和返回进行了类型限制
• 引入了泛化类型（Generic Type，简称泛型）和泛化函数(Generic Function, 简称泛函)

问题动机

在标准的遗传编程中，其假设了一种封闭性(closure)：任何函数都可以处理来自其他函数和端点的返回值类型。这种封闭性的设计让遗传编程并不适合处理混合的数据类型，且会损害遗传编程的性能。

• 函数集和端点集的设计
  在过去，Koza非常小心的定义了函数集和端点集，以减少这种限制性。比如在布尔函数的设计上，为了避免返回产生布尔类型的数值，Koza直接将判断语句整合进了函数，使用了类似IF-LESS-THAN来替代LESS-THAN之类的函数，如此判断语句并不会单独返回布尔类型。但是这种方式的使用条件比较局限，并不是所有的函数都可以通过很小心的设计来绕开使用或者返回多种数据类型。

• 动态类型
  第二种方式是使用动态类型(dynamic type)，让函数强制兼容不同的类型。这种动态类型的实现方式有两种，第一是参数多态(parametric polymorphism)，也就是同一个函数根据不同的参数类型执行不同的操作并且返回不同的类型的值；第二种方法是当函数出现类型错误时，让函数返回Flag标识并在评估个体时给予高惩罚。
  第一种方法在问题符合自然逻辑的情况下表现较好，比如让函数同时支持复数和实数的计算，可以将实数看做是虚部为0的复数。但是对于那些不符合自然逻辑的函数设计，有时候即便是可行，也不太可能将不同类型的变量泛化为新的数据类型的一部分。（比如上面例子中将实数泛化为复数） 此外，设置错误标识是保证动态类型的函数可以强制兼容非法的类型，但是这样做会花费过多额外的开销在那些类型非法的个体上。

• 强类型
  第三种解决标准遗传编程封闭性的方法是使用强类型(constrained types)，限制突变操作始终生成合法的树。在Koza版本的遗传编程的“高级功能”中，Koza指定了每一个函数所支持使用的端点集。

STGP借用了强类型这一思想，但是和Koza的版本不同的是，STGP中并非为每一个函数指定适合的端点集，而是指定了每一个函数的声明和返回的类型，通过指定类型来限制语法合规。这样做的好处是面对更加复杂的问题时无需为每一个函数都分别指定端点集，免去了这部分所需要的先验知识。

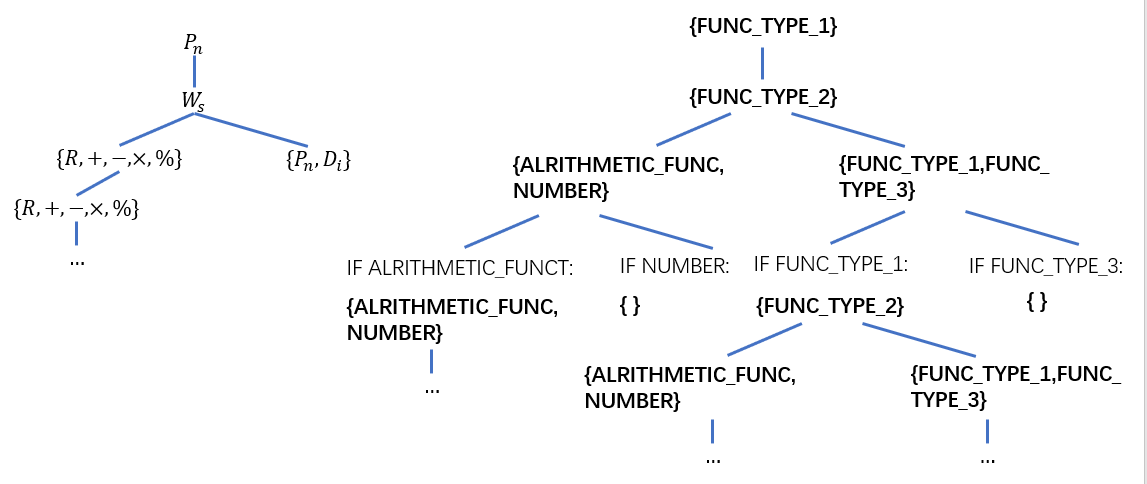
(左：Koza的强类型，右：STGP的强类型)

与之出现的新问题是，有一些函数的表现相同，但是需要支持的输入或者返回的类型不同。比如VECTOR_ADD_3表示1×3的向量相加，而VECTOR_ADD_4表示1×4的向量相加，同样是向量加法，但是因为输入的数据类型不同而需要反复定义功能类似的函数。为了避免这个问题，改进的STGP中引入了泛型和泛函。引入泛型和泛函的另一个动机是为了让程序可以通过创造小的程序逐步累计来创造足够大和复杂的程序。泛函可以作用于相对广泛的类型上，这样有利于代码重用。

基本的强类型遗传编程

个体表示和初始化

个体表示

在基本的STGP中，所有构成个体的元件(函数和端点)都有自己的类型。每个函数限制了返回值和声明的类型。此外，为了近一步控制使用多种数据类型，还额外规定：

• 树的根节点返回的类型和目标问题要求返回的类型相同。
  
• 父节点需要的声明的类型和子节点需要返回的类型相同。
  

一个关于个体表示的例子是，如下图，如果函数集为{DOT-PRODUCT-2,DOT-PRODUCT-3,VECTOR-ADD-2,VECTOR-ADD-3,SCALAR-VECT-MULT-2,SCALAR-VECT-MULT-3}，端点集为{V1,V2,V3},V1和V2的类型为VECTOR-3;V3的类型为VECTOR-2，问题要求返回的类型为VECTOR-3.
那么如下展示了合法的个体和不合法的个体：

初始化

初始化过程中STGP存在两个限制：

• 每个节点的返回值与其上层节点的所要求的声明的类型相同。
  
• 生成过程不会选择让子树非法的节点，如果没有可以选择的节点，那么会尝试其他的生成深度和生成方法。

比如如下的个体的生成方式展示：

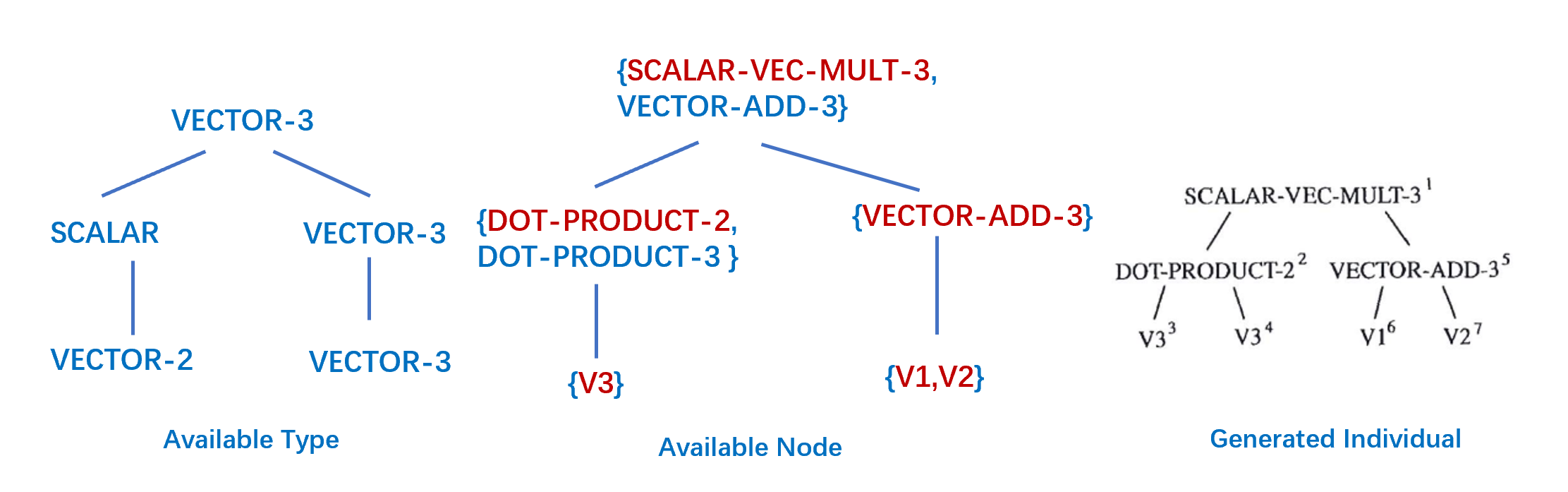
由于问题需要返回VECTOR-3，因此根节点可以选择函数SCALAR-VECT-MULT-3或者VECTOR-ADD-3，此处随机选择SCALAR-VECT-MULT-3； SCALAR-VECT-MULT-3的声明需要一个标量和一个类型为VECTOR-3的向量，对于结果返回为标量的函数，可以选择DOT-PRODUCT-2,DOT-PRODUCT-3，此处随机选择DOT-PRODUCT-2；返回VECTOR-3的函数只有VECTOR-ADD-3；
对于DOT-PRODCT-2，其声明是两个VECTOR-2的向量，只能选择V3； 对于VECTOR-ADD-3，其声明是两个VECTOR-3的向量，可以选择V1或者V2.

为了实现第二个限制，STGP必须遍历完所有可以选择的节点。STGP的实现方式是将每一层级所有可用的类型都以表格的形式存放，并且以链表的形式连接。
实现的伪代码如下：

depth = 1 #对于深度为1的类型表
for j in terminal_set:
  if type(j) not in table_entry(depth):
    table_entry(1).append(type(j)) # 将terminal set中的类型加入第一张表

for depth in [2, Max_Depth]:
  if using_growing_method==TRUE: # 如果使用了growing做初始化方法
  # 那么将上一张表的所有类型加入下一张表
  for k in function_set:
    table_entry(depth).append(table_entry(depth - 1)) 
    # 如果这个函数的声明类型在上一张表，但是返回类型没有在这一层的类型表中
    if (return_type(k) not in table_entry(depth)) & (arg_type(k) in table_entry(depth - 1)):
      table_entry(depth).append(return_type(k)) # 加入返回类型

遗传操作

突变

突变的操作和标准遗传编程类似，但是突变中新生成的树也需要遵守初始化生成树的原则。

交叉

交叉的第一个交叉点可以随机任选，但是第二个交叉点的选择上需要选择和第一个交叉点对应子树的类型相同，也就是交叉点所属的父子树所需要的声明的类型相同。

泛化函数和泛化类型

基本的STGP的最大的问题是，即便是所要求的函数的功能类似，但是因为输入类型的不同需要创建多个功能类似的函数。比如矩阵加法，就需要对输入的不同维度的矩阵分别创建不同函数。这个问题可以通过使用泛化函数解决(generic function)。泛函是一种参数多态，它是一种可以处理多种不同输入类型的函数。

上表展示了泛型和泛函的使用例子：

Function Name	Argument Type	Return Type
DOT-PRODUCT	VECTOR-i VECTOR-i	FLOAT
VECTOR-ADD	VECTOR-i VECTOR-i	VECTOR-i
MAT-VEC-MULT	MATRIX-i-j VECTOR-j	VECTOR-i
CAR	LIST-OF-t	t
LENGTH	LIST-OF-t	INTEGER
IF-THEN-ELSE	BOOLEAN t t	t

需要注意的是，STGP中所有的泛型函数只能有一个返回类型。
在泛函运行的过程当中需要确定输入一个固定的输入类型，这一过程称为实例化(instantiate)。泛型函数在个体树被生成(种群初始化阶段和变异中随机生成的子树)的过程中被实例化。在实例化之后这个函数会一直以实例化运行。
引入泛型函数后，需要对STGP作出两点改变：

• 第一点是，在没有泛型函数时每一个树的深度的类型是通过表得出的，在生成过程中需要检查树的声明类型是否在table_entry(depth - 1)返回类型是否在table_entry(depth)。引入泛型函数后，就需要考虑更多的可能性，于是每一个表中就需要加入所有的合法的可能组合类型：
  

  # 对于所有可以组成函数声明的类型组合
  for k in [combination of types in table_entry(i-1)  into arg_types in the function]:
    # 如果这样的类型组合是合法的，并且不在table_entry(depth)中：    
    if (arg_type_valide==1) & (return_type(k) not in table_entry(depth)):  
      table_entry.append(return_type(k))

• 第二个改动来自于生成树的过程。在生成树的过程中需要进行的类型检查在引入泛型函数之后也需要尝试所有可能的类型组合：
  

  for k in [combination of types in table_entry(i-1)  into arg_types in the function]:
    if arg_type(k) is valid :
      arg_type_valid = 1
    else:
      arg_type_valid = 0

泛型

泛型并不是一种数据类型，而是泛函支持的可能的数据类型的集合。泛型在树的生成过程中被视为是一种数据类型，但是在评估过程中由于实例化而视为是具体的值。使用泛型的目的是为了消除遗传操作中可能的非法性，同时减少了对先验知识的依赖和可能存在的先验偏见（避免了因为指定数据类型而导致的偏见）。有了泛化函数和泛型之后，遗传编程真正学习的是函数本身的结构。

VOID类型

VOID是一种特殊的数据类型，表明这个函数只是执行一系列操作，不返回任何数据。虽然一个函数可能既有作用(side effect)也要返回值，但是如果一个函数只执行命令而不返回任何值也能工作的话，那么就应该有一个单独的存储过程来执行这些作用。这也可以看做是减少偏见的一种方式，在这里指的是更简单的、不需要任何返回的解决方案。

本地变量

STGP同样支持本地变量。本地变量的类型由用户直接指定。本地变量的值的传入和传出是通过两个函数GET-VAR和SET-VAR进行的，每一个本地变量被创建之后都会自动创建属于自己的GET-VAR-i和SET-VAR-i。SET-VAR-i用于让本地变量i的值自动等于声明；GET-VAR-i用于返回本地变量i的值。

错误处理

STGP采用了一些机制来保证避免了类型错误。STGP中一些用于避免其他在执行函数时出错的方式的大体思路是，函数在（除了VOID函数外）运行过程中总会返回指向数据的指针，当函数运行过程出现错误时，设定函数返回一个NULL指针并停止运行这个函数。
STGP中一些常见的错误即处理如下。

奇异矩阵的逆

在数学上，奇异矩阵是不可逆的，即不存在满足矩阵乘法逆运算的逆矩阵。 因为逆矩阵的存在要求矩阵的行列式不为零。
Koza的方式是如果矩阵逆的操作对象是奇异矩阵，则对其进行“伪求逆”操作，即返回这个矩阵的特征矩阵。这样做的问题是当评估的数据中含有奇异或者非奇异矩阵时，保护的逆操作计算可能会对非奇异/奇异矩阵带来错误的结果。
因此，更好的办法是直接返回错误标识。

错误的列表元素

LISP语言中的CAR函数用于返回列表中的第一个元素，如果表为空则返回NULL。但是CAR函数要求返回值的类型需要与列表中元素的类型一致。在STGP中，当CAR所要求的一致性不能够被满足时，返回错误标识。

零为被除数

在Koza的版本中，当零作为被除数时会返回1. 但是在STGP的实验中并未涉及任何标量除法，因此 这个错误类型不会出现。

超时

为了确保评估工作不会因为评估某一个个体而陷入困境，STGP对评估的最长时间设定了一个与问题相关的限制。某些函数会检查个体评估是否超时，如果超时则返回错误标识。