PolyGP：一种多态遗传编程

PolyGP是由Tina Yu和Chris Clack^[1]共同设计的一种遗传编程算法。PolyGP借用了STGP^[2]中的参数多态的思想并进一步延伸，并使用了Robinson的合一算法(Unification Algorithm)^[3]改进了STGP中创建个体为了符合类型合法而导致的链表式结构的问题。PolyGP中最大的改动是将Koza的标准遗传算法中的个体表示从LISP语言的S-expression迁移到了Lambda演算(λ-calculus)中，并依据科里化(Currying)的个体结构将交叉迁移到了新的表现形式中。这些改动使得遗传编程可以真正学习程序的结构而不受变量和变量类型的限制。

背景知识

多态

多态(Polymorphism)是编程的一种程序特性，是指为不同的数据类型实体提供统一的接口，或者用单一的符号来表示不同的类型。多态有特设多态、参数多态和子类型三种。此处PolyGP和前身STGP使用的是参数多态(Parametric Polymorphism)，指的是一个类型或者多个类型不靠名字而是靠可以标志任何类型的抽象符号。在PolyGP中，多态指的是一个函数可以接受多种类型作为函数的输入(参数)或者接受多种类型作为函数的输出。
传统的模块化遗传编程的方法比如Koza的ADF及其后续的EDF、ARL都是单态的，每一个封装好的模块函数中的每一个参数或者返回只能支持一种特定的类型，比如void mono_func_demo(int,char)。而PolyGP和STGP中的函数中每一个参数或者返回都支持多种可能的类型，比如{int, char} poly_func_demo({str,int},{float,str,int})。

实例化和语境实例化

PolyGP中的多态函数在定义中使用了一些临时的占位符（泛化类型变量、泛化冗余类型变量、临时类型变量等等），这些临时的占位符被具体化为某一个特定的值的过程称为实例化(instantiation)，也就是多态函数到单态函数的过程。 比如{int, char} poly_func_demo({str,int},{float,str,int}) -> char poly_func_demo(int,int) PolyGP中采用的实例化的策略为语境实例化(contextual instantiation)，即当一个占位符被实例化的时候，多态函数中其他出现这个占位符的地方也会被实例化为相同的值，多态函数变为单态函数。但是在此次调用结束后函数集中的单态函数将会重新退化到原来的多态函数。
PolyGP中规定语法树中实例化的顺序为先上后下，先右后左。

Lambda演算^[4]

Lambda演算(λ-calculus)是一种在结构上极其简单的编程语言。

Lambda演算由变换规则(transformation rule)和单函数定义(single function defination)两部分组成，任何可计算的函数都可以用这种方法进行表示，其类似于图灵机(Turing machine)，但是相比于图灵机更强调变换规则的使用。变换规则利用了编程中替换(substitution)的思想。

表示

要解释变换规则，首先需要了解Lambda演算中的表示(expression)。表示是Lambda演算中的计算实体，它可以是一个变量或者是函数。Lambda演算的表示可以通过如下的递归进行定义：

<expression> := <name>|<function>|<application>
<function> := λ<name>.<expression>
<application> := <expression><expression>

在Lambda演算中，称变量为name——它只是一个用于描述的名字，没有任何作用能力。
Lambda演算中不同成员之间的交互依赖于函数function，任何感兴趣的单位都可以被视为函数，如此这些单位将具有使用变换规则的能力。函数表示为λ<name>.<expression>，其中.之前的是函数的参数变量，由λ限定表示这个变量是该函数的“自变量”，后面的表示expression则是函数体的body部分，描述函数的行为。
应用application是变换规则的具体化，<application> := <expression1><expression2>的表示相当于是把expression2的结果带入expression1中。
比如下面的例子：
\[(λx.x)y\] 实际上相当于是将变量\(y\)带入到以\(x\)作为自变量的函数中，因此这个应用的结果是将\(y\)替换\(x\)，得到最后的函数结果为\(x\)。有时候，这样的替换也可以简单表示为\([y/x]x\)。
函数的推演过程用\(→\)表示，因此上述应用的计算过程可以表示为： \[(λx.x)y→λy.y→y\]

自由变量

Lambda演算中所有的<name>对函数而言都是本地变量，函数中那些没有被λ限制的变量称为自由变量(free variable)，例如：\((λx.xy)\)中\(y\)是自由变量。
在如下的情况中<name>是一个自由变量：

• <name>单独存在，比如\(a\)在\(a\)中是自由变量。
  
• <function>中没有被\(λ\)固定。
  
• 对于<application>，如果一个变量在前后任意一个<expression>中是自由变量，那么其在<application>中也是自由变量。

替换

替换是应用的化简原则，其规则是：
对于<application> := <expression1><expression2>，将<expression1>中所有的自由变量用<expression2>替换。如果<expression1>中用λ固定的部分与<expression2>重名，那么则需要改名。
下面举了一个推演<application>的例子：
\[(λx.(λy.xy))y→(λy.(λy.xy))→(λy.(λt.xt))→(λt.yt)\]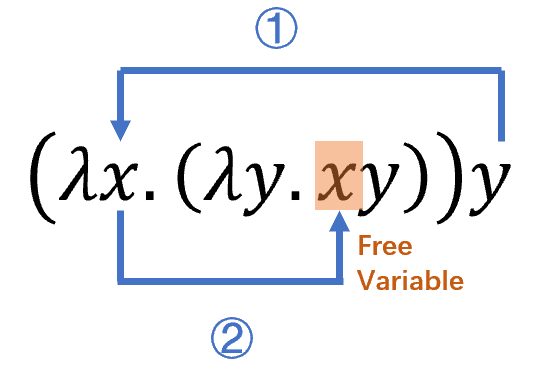

科里化和偏函数

柯里化(Currying)是把接受多个参数的函数变换成接受一个单一参数（最初函数的第一个参数）的函数，并且返回接受余下的参数而且返回结果的新函数的技术。 在直觉上，柯里化声称「如果你固定某些参数，你将得到接受余下参数的一个函数」。所以对于有两个变量的函数，如果固定了一个变量，就得到有一个变量的函数。 柯里化在理论计算机科学中提供了一种研究带有多个参数的函数的方式，尤其在只接受一个单一参数的lambda演算中。

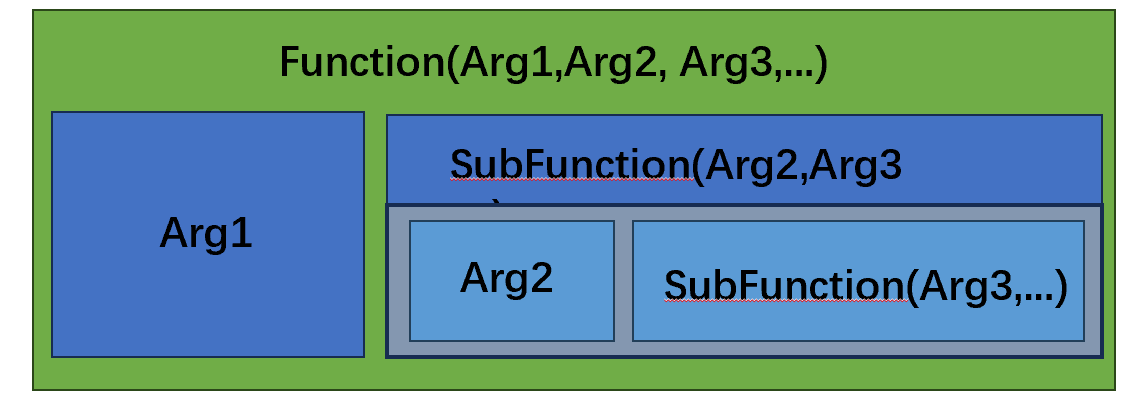
例如，以下是一个柯里化的示例函数：

var foo = function(a) {
    return function(b) {
        return a * a + b * b;
    }
}

// 调用上述函数：
var result = foo(3)(4); // 结果为 25

其中子函数的部分也可以被提取出来独立运行，被视为是父函数的部分表达，称为偏函数(Partial Application)^[5]。偏函数为PolyGP提供了在lambda演算下实现交叉的可能。

有类型的Lambda演算

标准的Lambda演算是没有数据类型的，但是后续有若干学者用各种方式实现了有类型的Lambda演算(Typed Lambda calculus)。PolyGP中使用的是Hindley–Milner类型推论算法^[6]。

• function和expression的类型
  在这种方法中，name、function和expression都具有类型，function和expression的类型表示为：
  \[F1^{σ1→σ2}\] 其中，\(σ1\)表示的是函数的参数类型；\(σ2\)表示的是函数的返回类型。
  PolyGP的论文中使用了科里化的表示方法：
  \[(F1^{σ1→σ2} ARG1^{σ1})^{σ2}\] 其中\(ARG1\)是函数\(F1\)的参数。
  使用科里化的表示方法的目的是为了更好的表示有多个参数的函数，如下面的函数\(F2\)拥有两个参数\(ARG1\)和\(ARG2\)，其类型分别为\(σ1\)和\(σ2\)，函数的返回类型为\(σ3\)，简单表示为：
  \[F2^{σ1→σ2→σ3}\] 展开表示为：
  \[((F2^{σ1→σ2→σ3} ARG1^{σ1})^{σ2→σ3} ARG2^{σ2})^{σ3}\]

  函数的嵌套需要满足子函数的返回类型应该是父函数的参数类型，如此才满足合法性。比如上面的函数\(F1\)的返回类型正好满足\(F2\)中\(ARG2\)的类型，因此可以实现\(F2\)中嵌套\(F1\)：
  \[((F2^{σ1→σ2→σ3} ARG1^{σ1})^{σ2→σ3} (F1^{σ1→σ2} ARG1^{σ1})^{σ2})^{σ3}\]

  这种表示方法可以被转换为树形结构，下图展示了上面的三个例子是如何被树形结构化的：

  

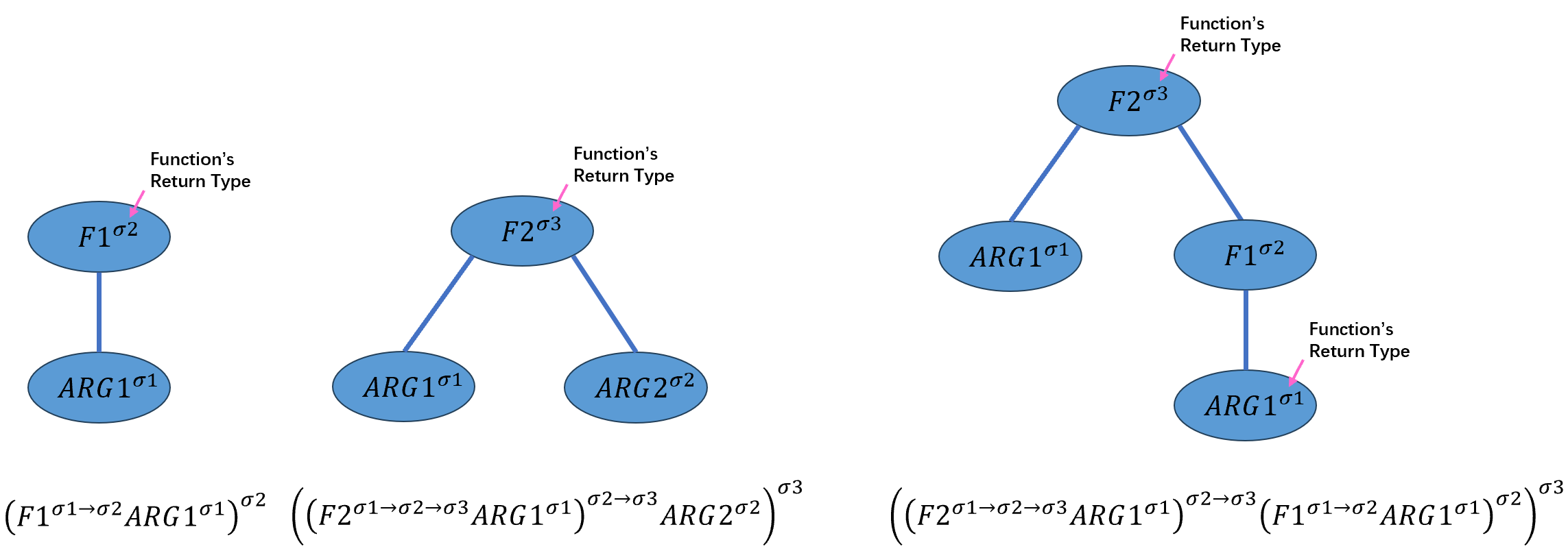
• application的类型
  应用application的类型可以根据expression的类型推理得出：
  如果expression1有类型\(σ1→σ2\)，expression2有类型\(σ1\)，那么一个应用<expression1><expression2>的类型就应该是\(σ2\)。

算法结构

PolyGP相比于标准GP最大的改进在于引入了类型系统(type system)，在种群初始化和遗传操作（下图中的evolvor和creator）两个阶段中用于保证所有的个体都是类型合法的。

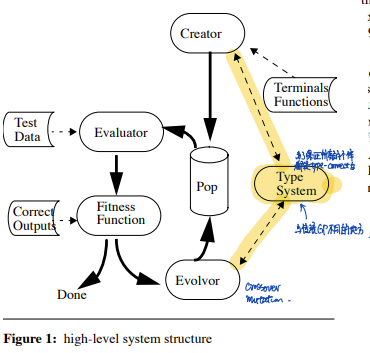
种群初始化与个体表示

PolyGP中的个体表示为有类型的lambda演算的函数。种群初始化的过程中调用了类型系统来检查类的合法性。

元素的类型

同STGP一样，端点集和函数集中的每一个元素（端点/基函数）都具有类型，PolyGP中的类型有如下5种：

σ::τ        build in type
  |v        type variable
  |σ1→σ2    function type
  |[σ1]     list of elements all of type σ1
  |(σ1→σ2)  priority
  τ::int | string | bool | generic_i
  v::dummy_i | temperary_i

• 内置类型\(τ\)：比如int，string,bool等等，除此之外还有泛化类型generic_i
• 类型变量\(v\)：包括冗余类型变量和临时类型变量，以下会详述
• 函数的类型\(σ_1→σ_2\)：表示函数的类型，在有类型的Lambda演算中已经介绍过
• 列表的类型\([σ_1]\)表示列表中所有元素的类型都是\(σ_1\)
• 优先级\(()\):用于表示类型推论的优先级

类型变量

此外，为了实现多态性，在PolyGP中引入了三种不同的类型变量用于在不同的阶段表示个体：

• 泛化类型变量(generic type variable)
  类型变量(type variable)是一种用于表示类型的变量，这个变量的具体值是某一种数据类型，比如x -> int。所谓泛化类型变量就是这个类型变量可以允许多种类型的具体值。泛化类型变量在进化的过程中永远不会被实例化，在进化的过程中会被看做是内置的类型。
  泛化类型变量用于在进化过程中表示函数集中的多态函数的类型。
  
• 冗余类型变量(dummy type variable)
  冗余类型变量用于在构建个体中表示函数集或者端点集中多态函数的类型。在创建个体的过程中每一次用到含有冗余类型变量的函数时，都需要对冗余类型的变量进行实例化。
  比如：已知函数集中的两个多态函数\(f1\)和\(f2\)的参数类型是一致的（或者两者的类型存在某种关联），但是并不对具体的参数类型值做限定，那么此时就用冗余类型变量\(α\)进行标记：\(f1^{α→[\alpha]}\),\(f2^{α→α}\)。创建个体的过程中如果要调用这两个函数，那么\(α\)将会被实例化为具体的类型，比如\(f1^{int→[int]}\),\(f2^{int→int}\)。
  在冗余类型变量实例化的过程中，会根据父函数所要求的类型实例化为特定的类型；如果没有要求(比如父函数只对子函数的返回类型做要求，并未对参数类型进行限制)，子函数的冗余类型变量将会被实例化为临时变量。
  
• 临时类型变量(temporary type variable)
  临时变量会在遗传操作的过程中根据其中一个亲本的类型进行实例化。
  需要在创建个体的过程中，如果需要一个冗余类型变量和一个临时类型变量类型相符(unify)，这个时候冗余类型变量会先实例化为一个特定的临时类型变量，之后再根据遗传操作实例化为其他的类型变量。

多态的函数和端点会使用冗余类型变量来进行表示。但是如果函数和端点是程序的参数或者输出，那么则使用泛化类型变量。

需要再次强调的是，PolyGP中使用的是语境实例化。

合一算法

个体创建的过程中，和STGP一样，要求个体要求其父函数的参数的类型与子函数的返回的类型相同。

这一规则是通过合一算法(unification algorithm)进行检查的。
合一是找到使两个给定表达式相等的替换的过程。具体而言，合一算法规定了两个表达式中的变量如果代换为相应的表达式之后是否可以等价。在类型系统中，合一算法可以规定在特定的实例化下两个类型变量是否被视为是合一的(unified)/等价的。
在合一算法中，定义替换(substitution)：
\[θ=\{(X_i,t_i),...\}\] 其中\(X_i\)是一个类型变量，\(t_i\)是一个特定的类型，比如\(\{(a,int)\}\).
对替换应用到一个函数类型(指形如为arg_type → return_type的类型)\(A\)的结果\(Aθ\)是这个类或者函数\(A\)中所有出现\(X_i\)的地方都被替换为\(t_i\)，比如：
\[α→α\{(α,int)\} = int → int\] 那么对于两个函数类型\(A\)、\(B\)，如果存在一个替换\(θ\)使得:
\[Aθ=Bθ\] 那么称两个函数类型\(A\)和\(B\)是合一的。
比如对于\(A:X_1→[string]\)和\(B:int→X_2\)，可以找到一个替换\(θ=\{(X_1,int),(X_2,[string])\}\)使得\(Aθ=Bθ\)，那么类型\(A\)和\(B\)是合一的。

有些时候两个类型可能会有不止一个替换可以使其合一，在这种情况下，合一算法会返回更为通用的替换。也就是说，合一算法会更倾向于返回含有类型变量的替换。

在个体生成的过程中，合一算法会始终检查每一级的子函数的返回类型是否与上一级的父函数参数的类型对特定的实例化目标合一。
在PolyGP中，合一化要求的替换必须要是有意义的，也就是说冗余类型变量和临时类型变量不能够做合一化。

种群初始化

PolyGP的个体生成使用的是Full初始化方法（即深度优先，在未达到深度前只选择函数集中的元素），此外还需要遵循合一算法的类型检查。
此外，PolyGP中还设计了一个回溯机制(trackback)：生成过程中无法找到满足特定类型的端点/基函数时，则返回到上一个合法的节点，重新选择该节点上的函数。

个体生成的例子

这个例子的要求如下：

Output Type: [G2]
Terminal Set: {L::[G1],NIL::[α],F::(G1→G2)}
Function Set: 
        { HEAD::[α]->α,
          IF-ELSE::bool -> α -> α → α,
          TAIL::[α]->[α],
          CONS::α->[α]->[α],
          NULL::[α]->bool,
          F::G1->G2,
          MAP::(G1->G2)->[G1]->[G2]}
Max Tree Depth: 3

其中α是冗余类型变量；G1和G2是泛化类型变量。

这里的F::(G1→G2)是一个高阶函数(high order function)，可以理解为一个零输入函数，作为端点使用。

某个个体生成的具体步骤（附图文解释和说明）

1. 首先选取一个函数IF-ELSE（图中用IF替代，作者此处写明为IF函数，疑似笔误），其需要三个输入参数类型分别为bool、α、α，由于程序需要返回的类型为[G2]，因此IF-ELSE的返回类型需要是[G2]，因此α需要被实例化为[G2]:
   \[(((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} ARG2^{[G2]})^{[G2]→[G2]} ARG3^{[G2]})^{[G2]}\]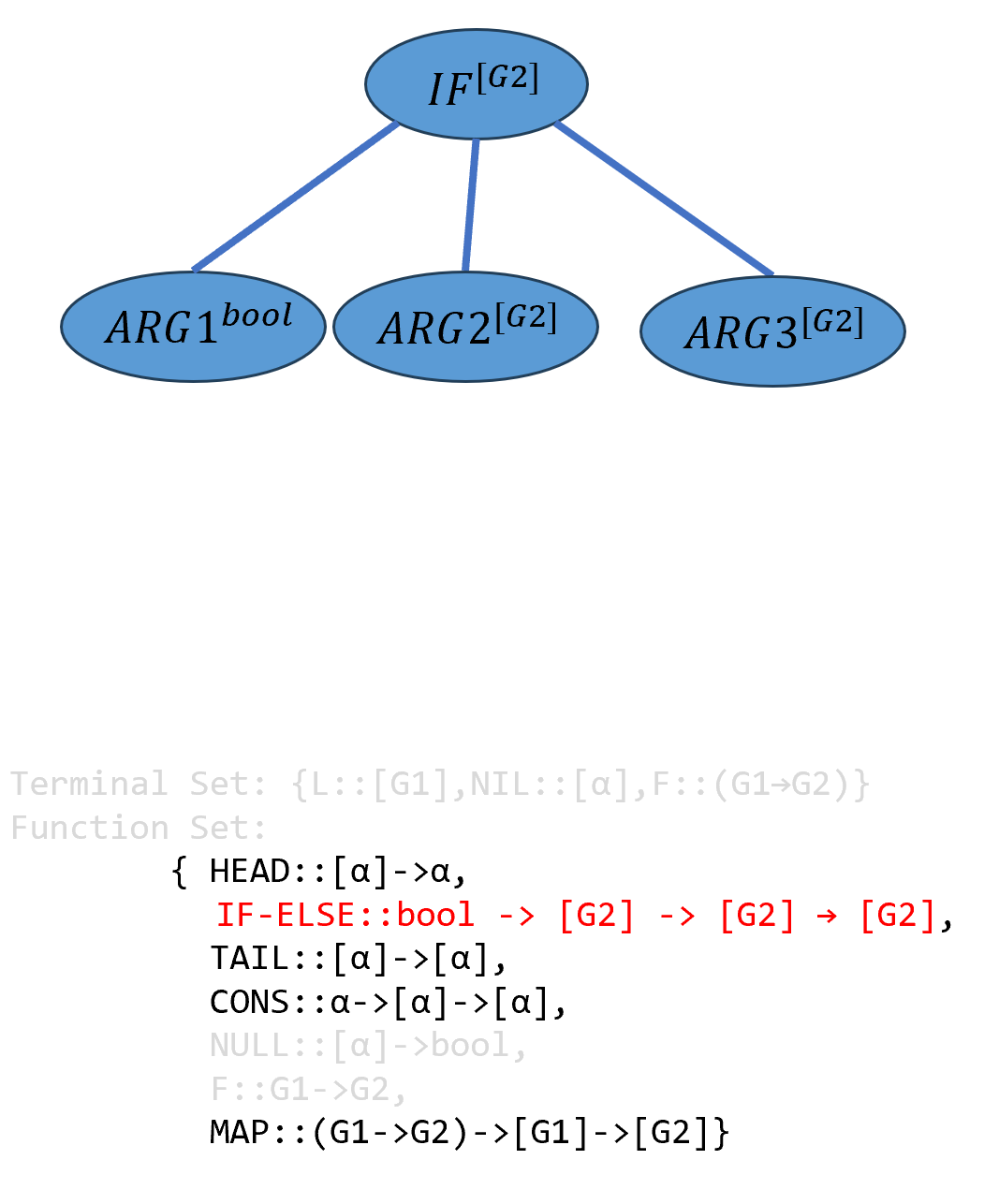

2. 根据先上后下，先右后左的原则，寻找函数集中合适的\(ARG3\)（即返回类型为[G2]的函数），此时类型系统随机选择了MAP函数作为\(ARG3\)，它的返回类型正好是[G2]，它引入了两个新的输入参数\(ARG4\)和\(ARG5\)类型要求对应为(G1→G2)和[G1]:
   \[(((IF-ELSE-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} ARG2^{[G2]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} ARG4^{(G1→G2)})^{[G1]→[G2]})ARG5^{[G2]})^{[G2]}\]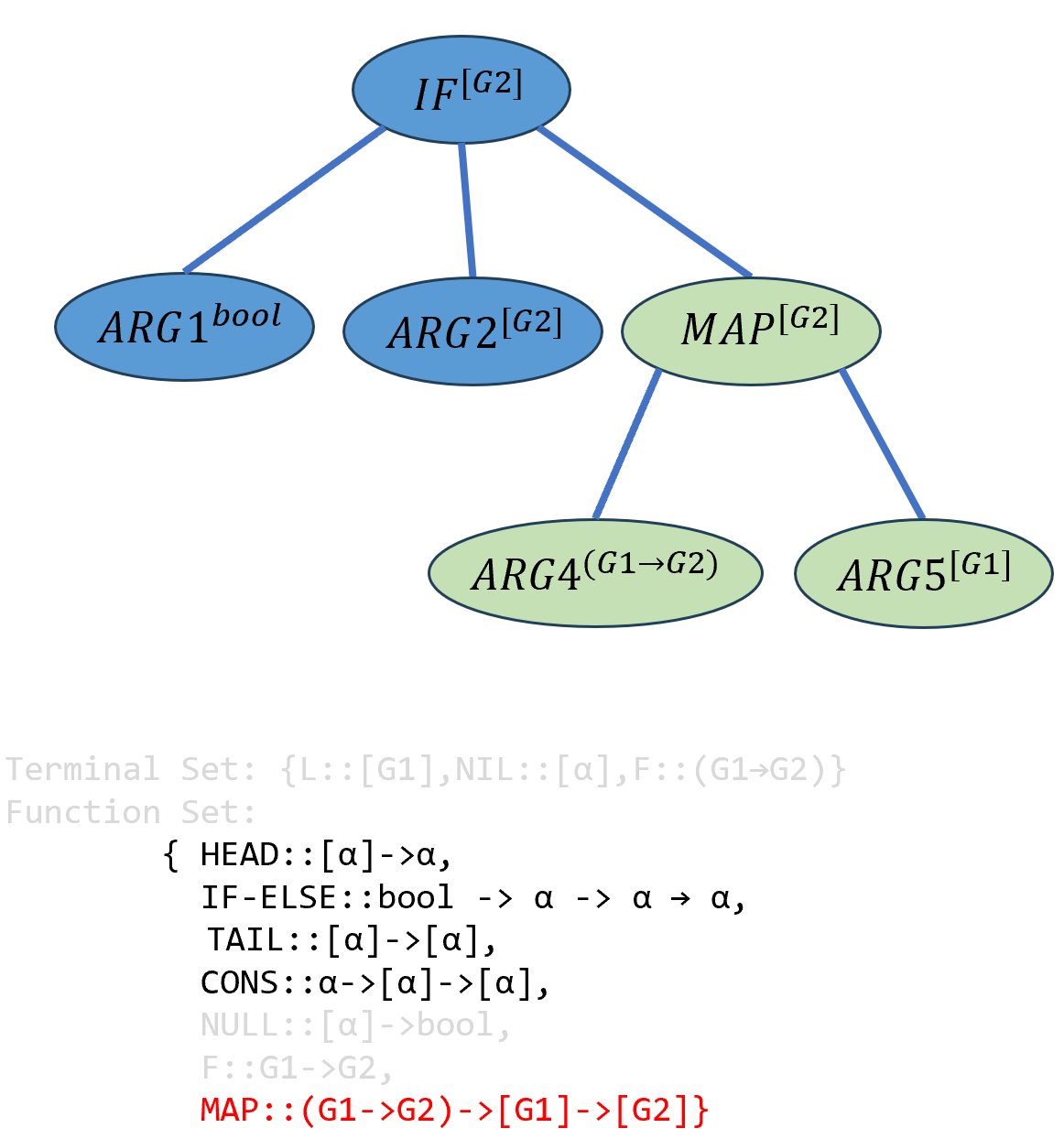

3. 由于达到了最大深度，于是开始选择端点，按照MAP函数的参数类型要求，只能用\(F\)填入\(ARG4^{(G1→G2)}\)：
   \[(((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool}) ARG2^{[G2]})^{[G2]→[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})ARG5^{[G2]})^{[G2]}\]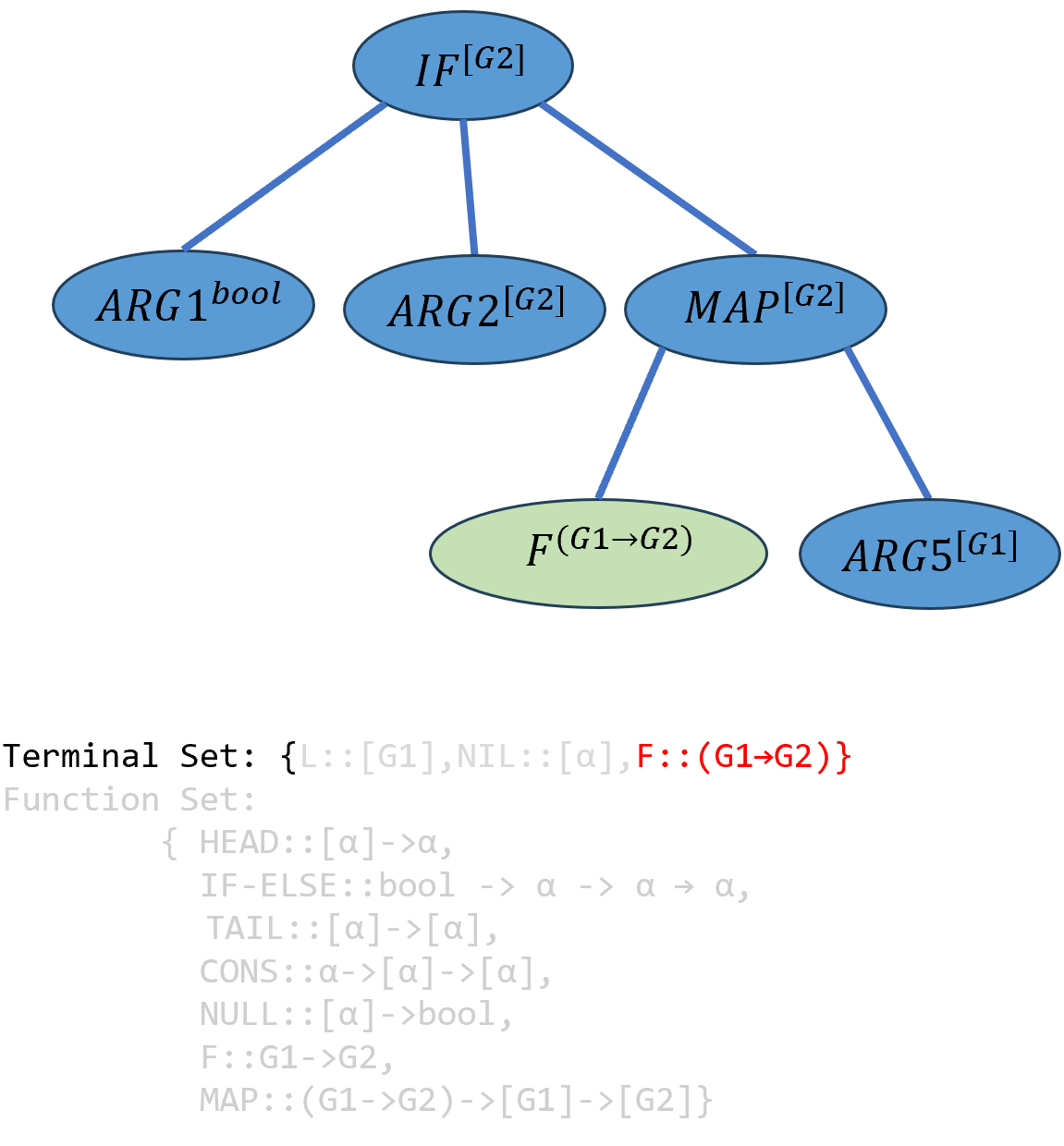

4. 同理只能用\(L\)填入\(ARG5^{[G1]}\): \[(((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} ARG2^{[G2]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]

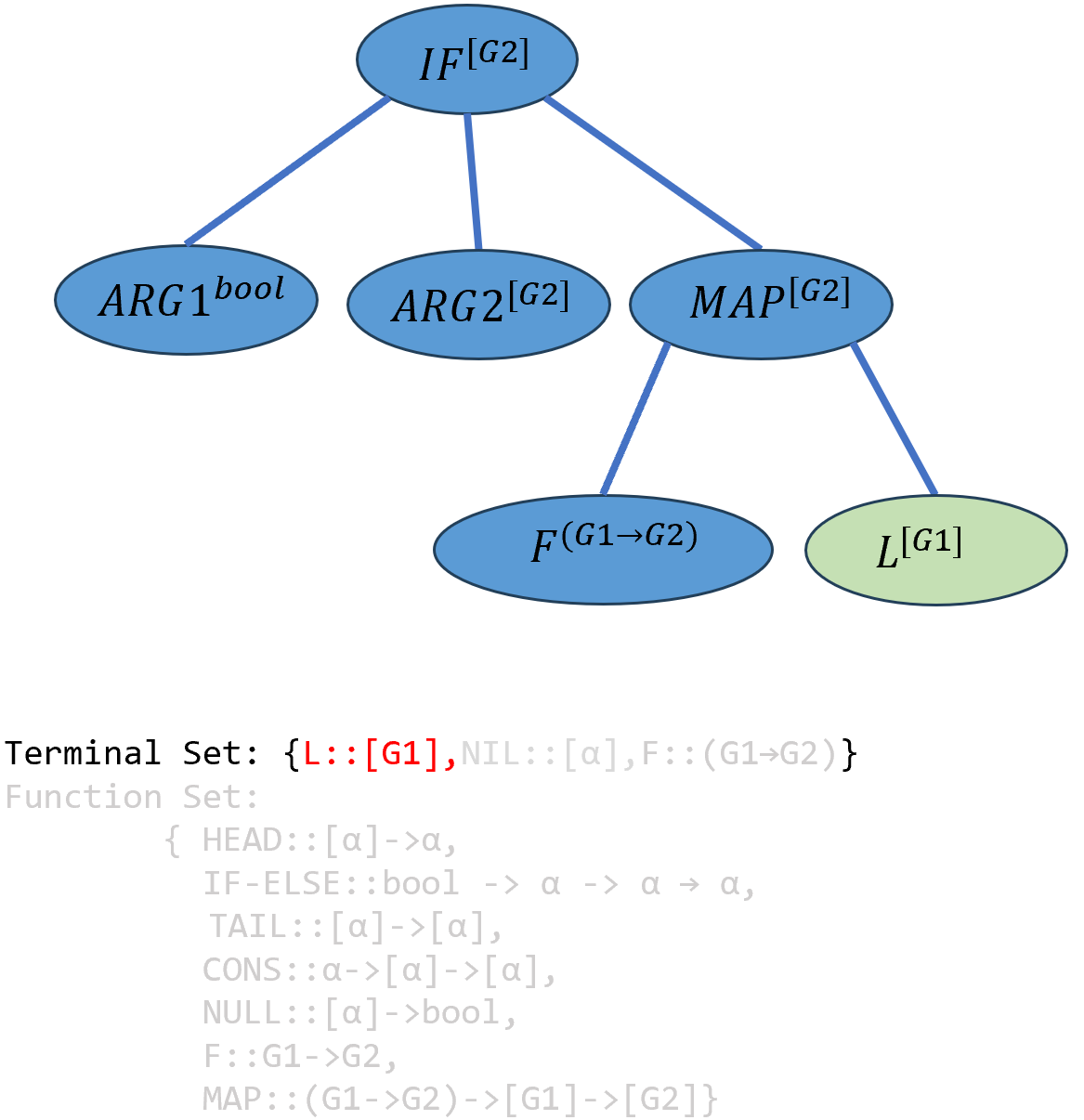
5. 接下来实例化\(ARG2\)，类型系统随机选择了IF-ELSE作为\(ARG2\)并引入了新的参数\(ARG6\)、\(ARG7\)、\(ARG8\)，这些参数的类型分别为:bool、[G2]、[G2].
   \[(((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} ((IFELSE^{bool→[G2]→[G2]→[G2]} ARG6^{bool})^{[G2]→[G2]→[G2]} ARG7^{[G2]})^{[G2]→[G2]}ARG8^{[G2]})^{[G2]})^{[G2]→[G2]} (((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]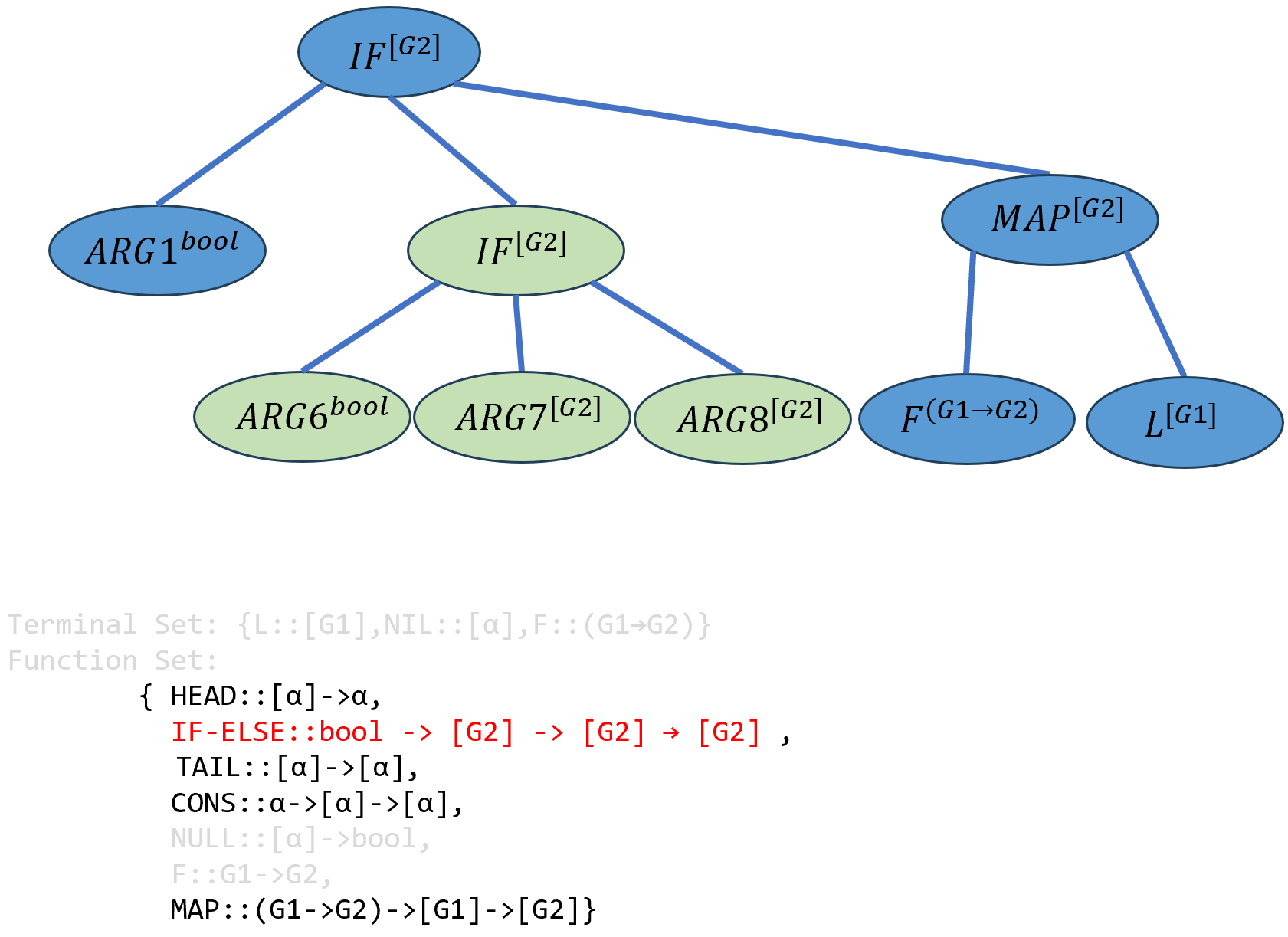

6. 达到最大深度，按照和3、4相同的方法，对\(ARG8\)和\(ARG7\)，要求类型为[G2]的端点，只能填入\(NIL\)，同时该函数中的\(α\)被实例化为G2:
   \[(((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} ((IFELSE^{bool→[G2]→[G2]→[G2]} ARG6^{bool})^{[G2]→[G2]→[G2]} NIL^{[G2]})^{[G2]→[G2]}NIL^{[G2]})^{[G2]})^{[G2]→[G2]} (((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]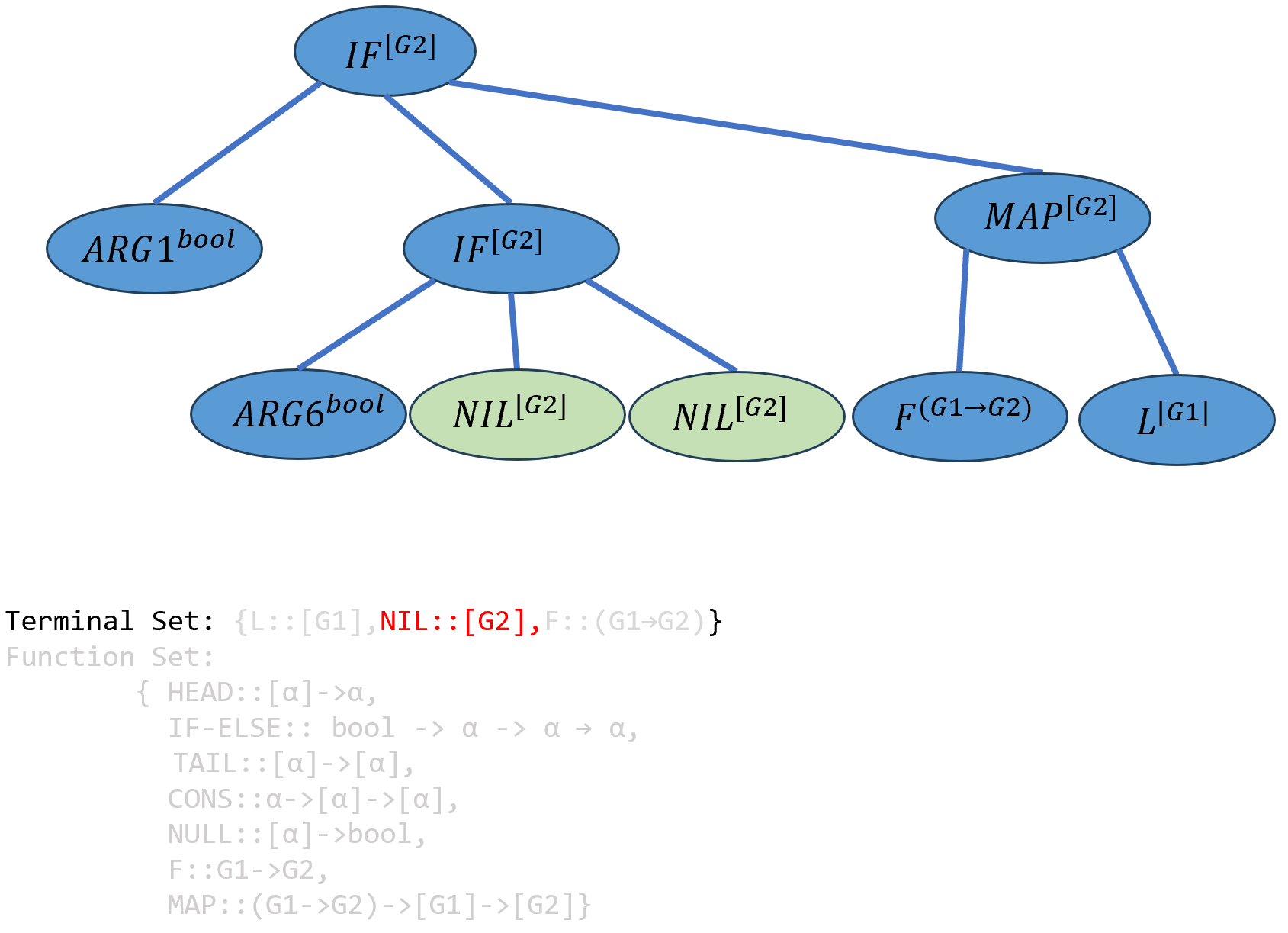

7. 对\(ARG6\)实例化，但是端点集中没有bool类型的端点，生成出错，因此退回到上一级函数生成的节点重新选择其他函数。
   

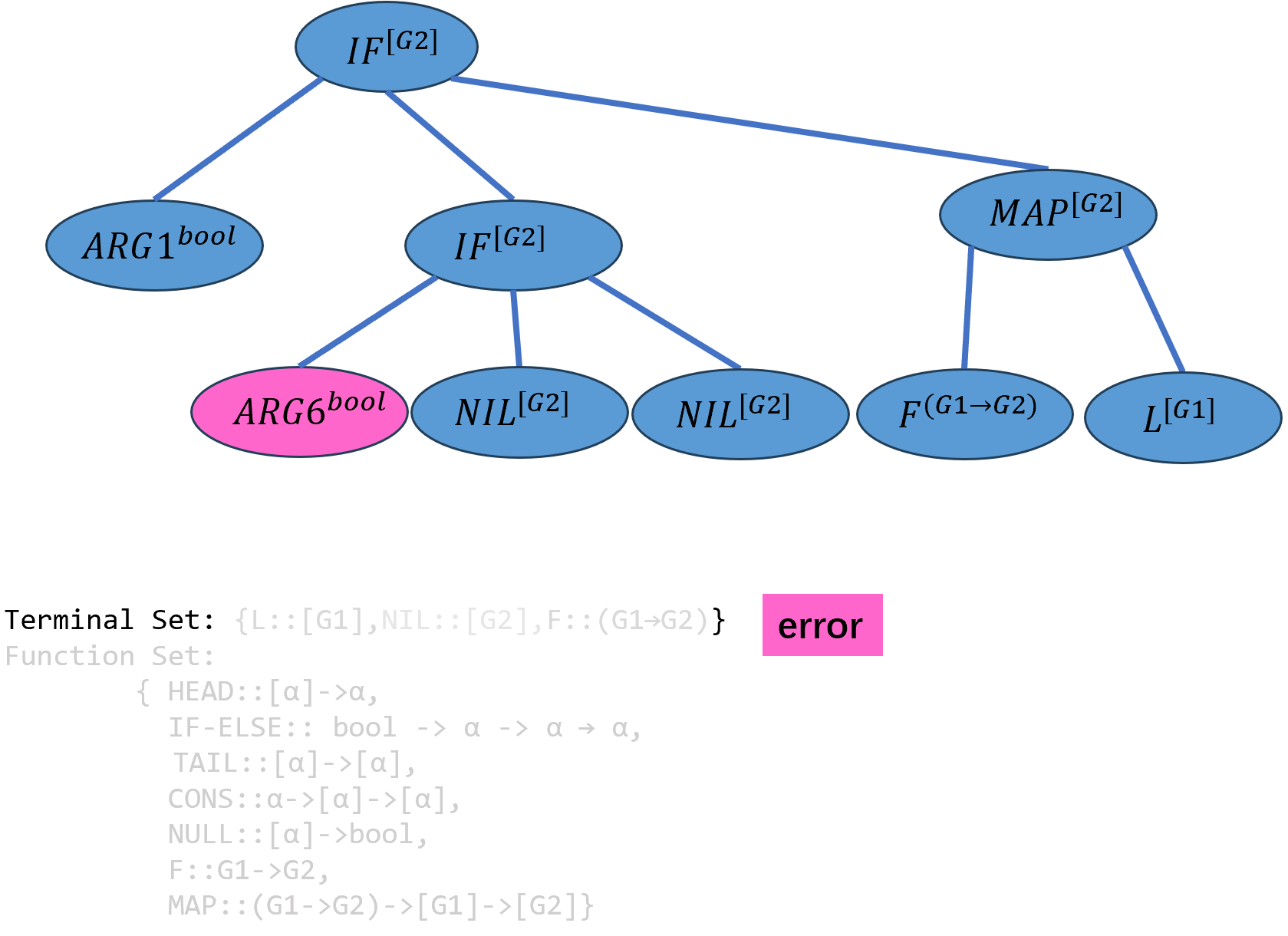
8. 重新选择\(ARG2\)的实例化，这次选择HEAD函数，该函数中α被实例化为[G2]，并引入新的参数\(ARG9\)，其类型为列表的列表[[G2]]:
   \[((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} (HEAD^{[[G2]]→[G2]} ARG9^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]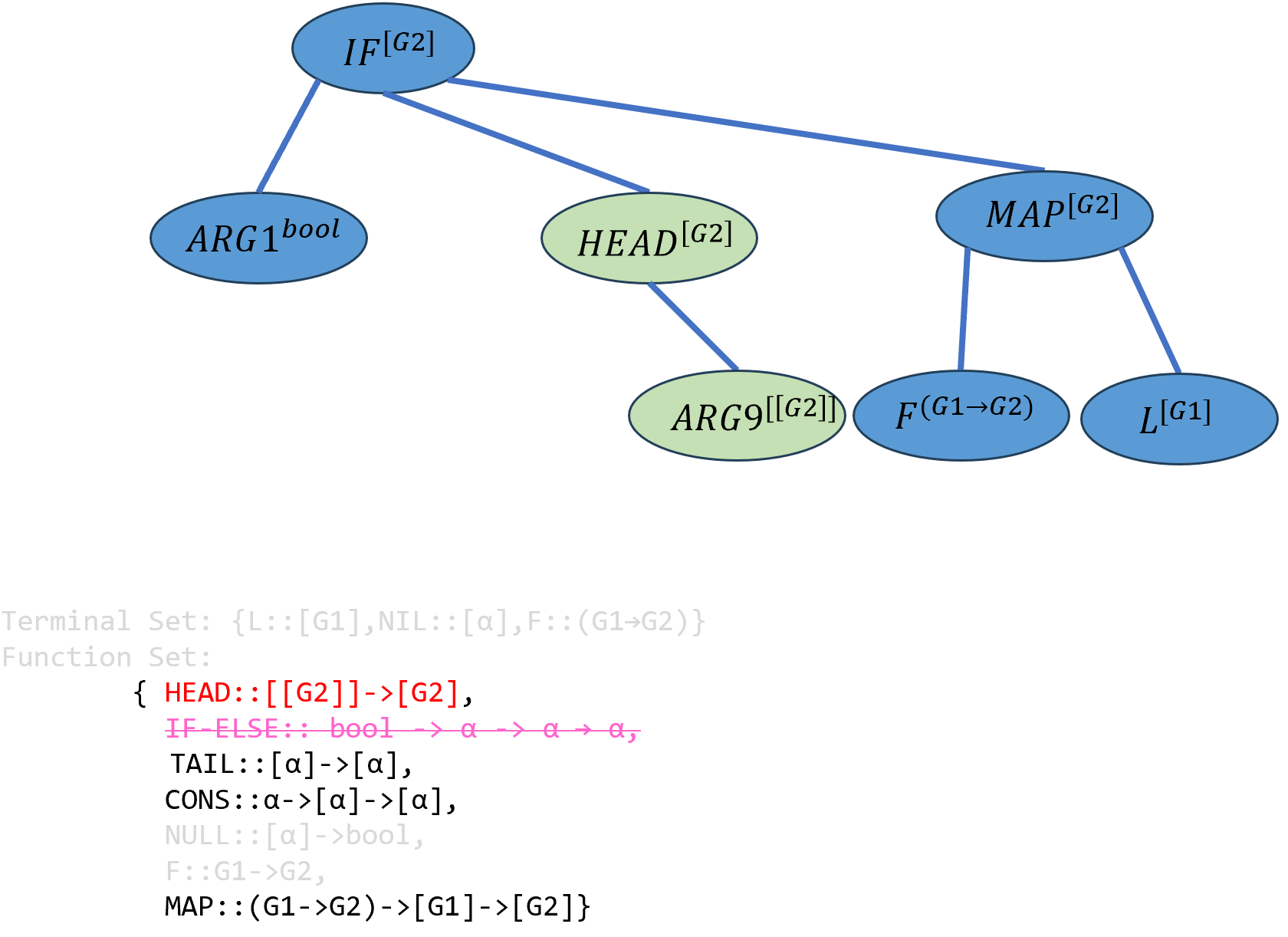

9. 实例化\(ARG9\)，只能填入\(NIL\)，同时该函数中的\(α\)被实例化为[[G2]]:
   \[((IF-ELSE^{bool→[G2]→[G2]→[G2]} ARG1^{bool})^{[G2]→[G2]→[G2]} (HEAD^{[[G2]]→[G2]} NIL^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]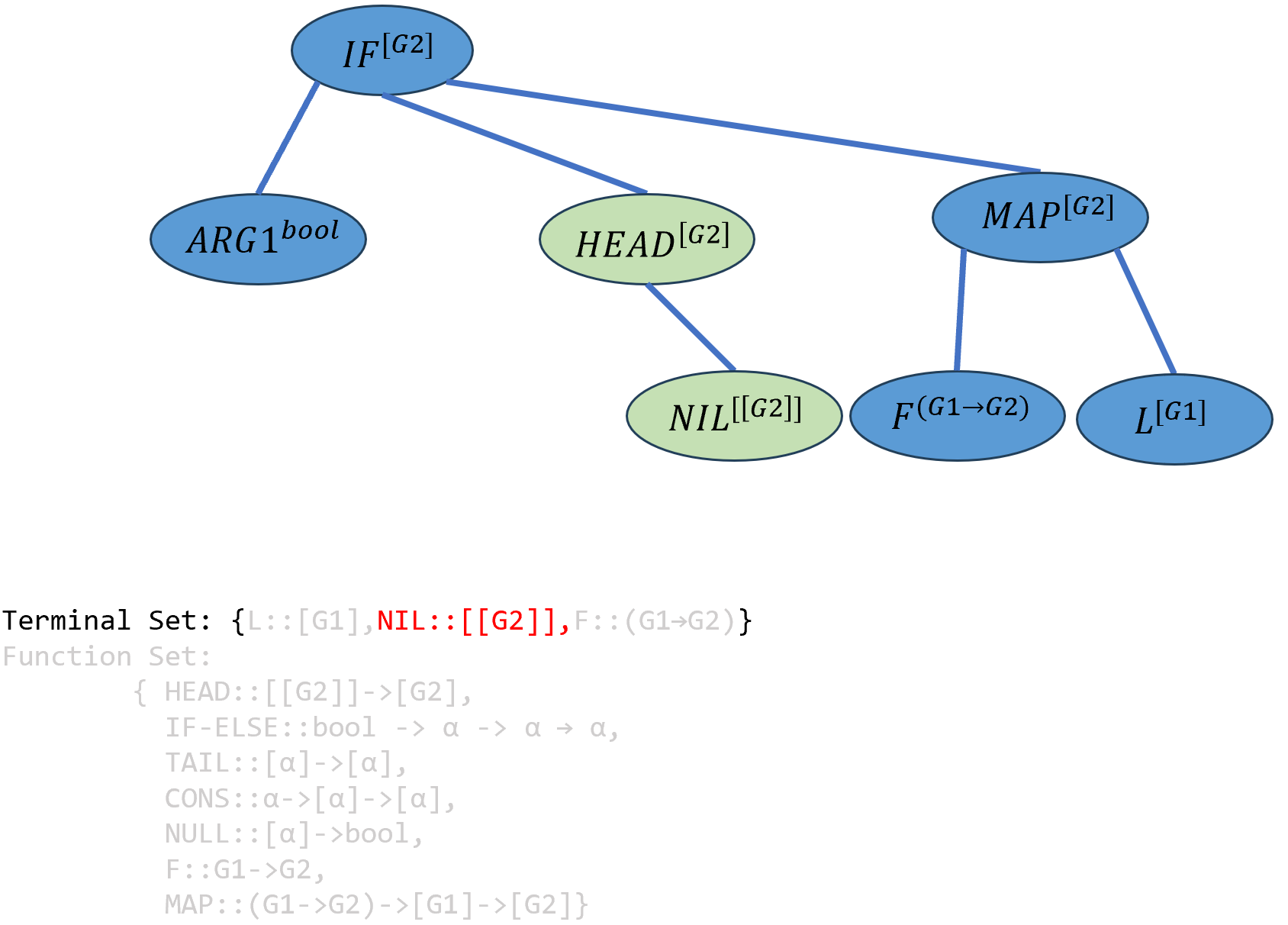

10. 实例化最左边的\(ARG1\)，由于\(IF-ELSE\)函数不能在此层出现，函数集中唯一的选择是\(NULL\)，由于其参数类型为α且并没有任何限制，按照冗余类型变量的机制，新建一个临时类型类型变量T1并将α实例化为这个类型变量。
    \[((IF-ELSE^{bool→[G2]→[G2]→[G2]} (NULL^{bool→[T1]} ARG10^{[T1]})^{T1})^{[G2]→[G2]→[G2]} (HEAD^{[[G2]]→[G2]} NIL^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]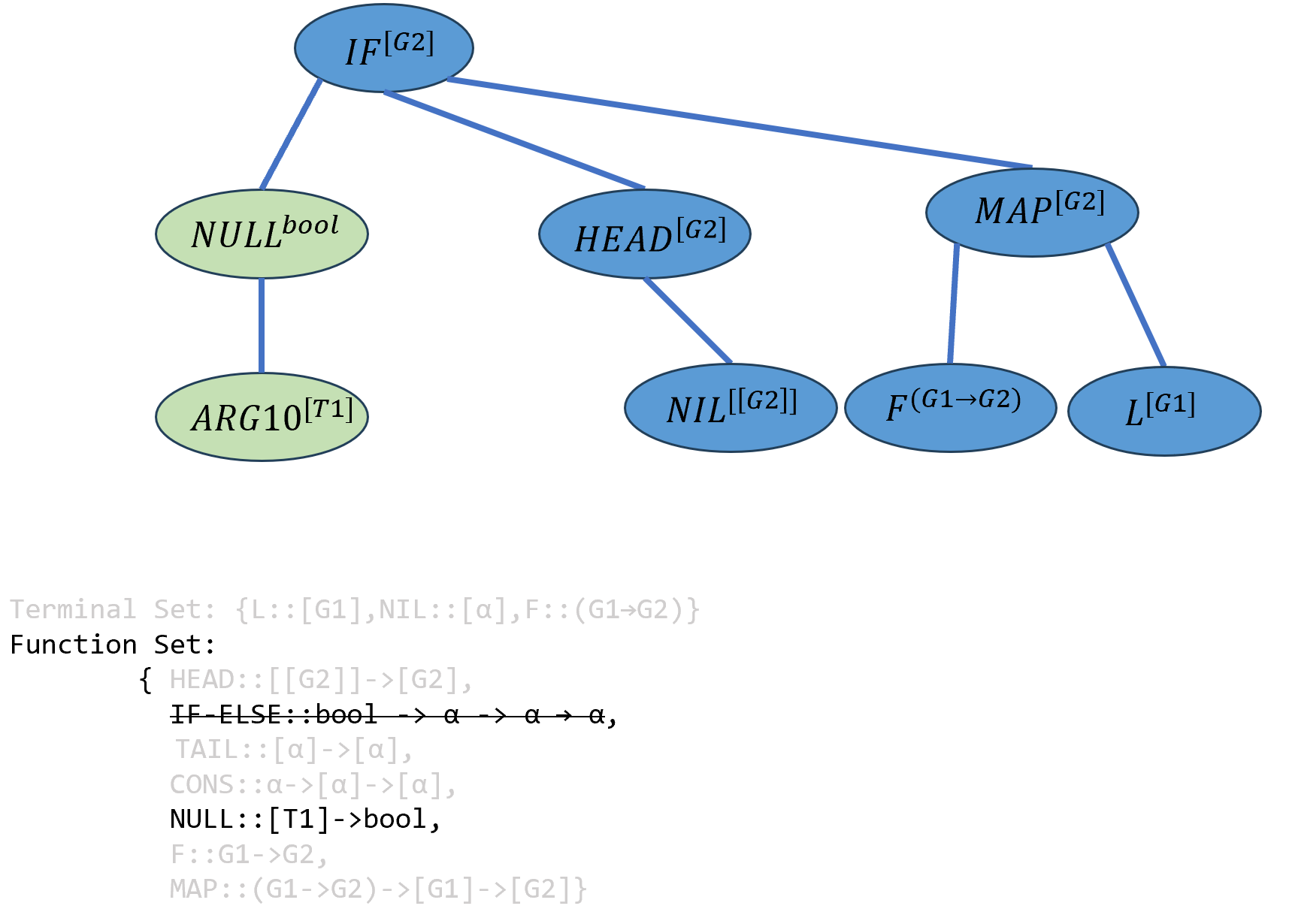

11. 实例化\(ARG10\)，其类型为[T1]应当是一个列表，因此\(L\)和\(NIL\)都符合要求，类型系统随机选择了\(NIL\)，由于\(NIL\)中的冗余类型变量α不能临时类型变量T1和进行合一化操作，此处只能将α实例化为新的临时类型变量T2.
    T2会在遗传操作中被实例化。
    \[((IF-ELSE^{bool→[G2]→[G2]→[G2]} (NULL^{bool→[T1]} NIL^{[T2]})^{T1})^{[G2]→[G2]→[G2]} (HEAD^{[[G2]]→[G2]} NIL^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\]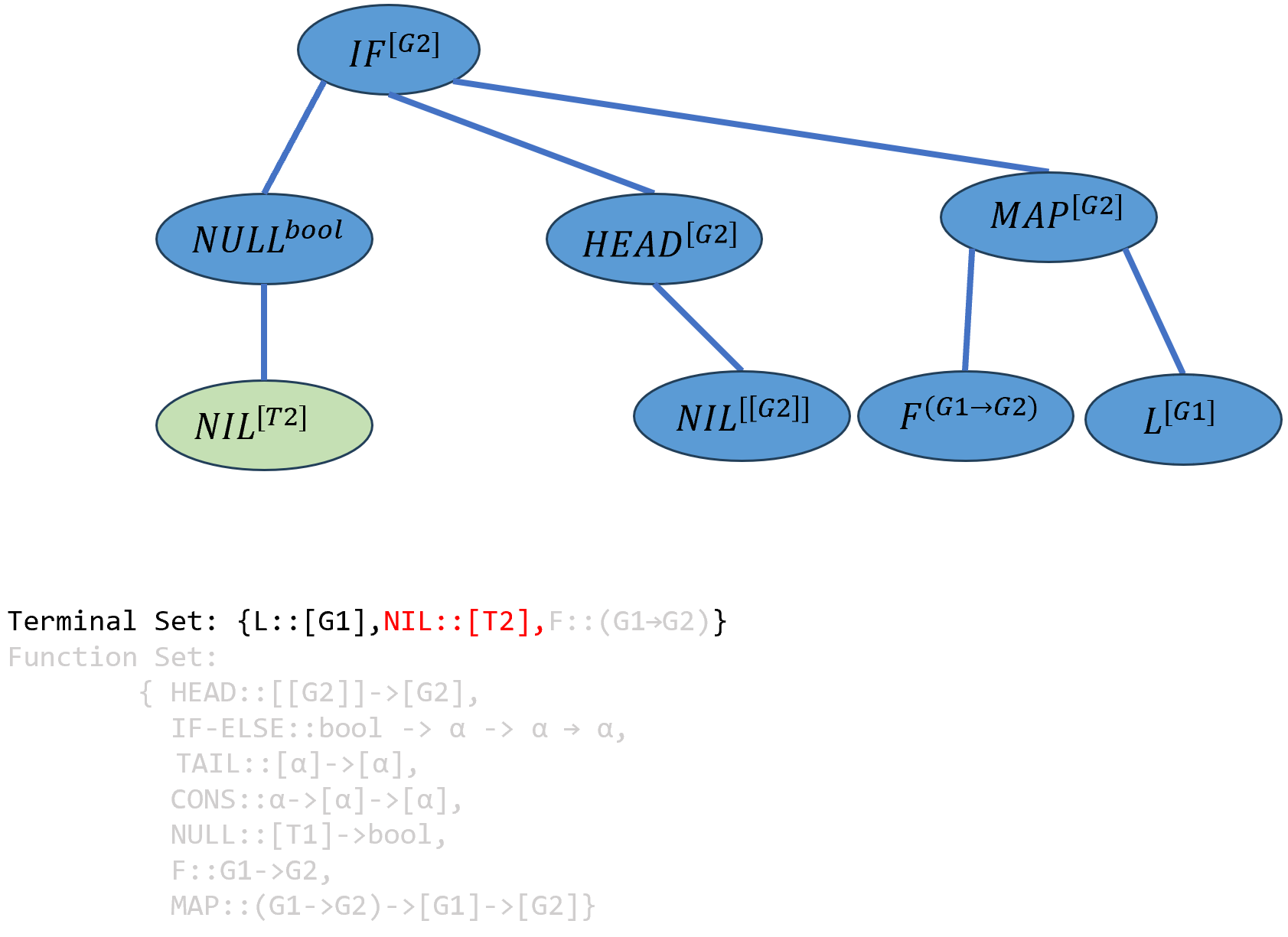

最终的个体为：

整个生成该个体过程的动画：

递归

PolyGP中允许个体含有递归结构，实现的方法也很简单，正在生成的个体会被命名然后放入函数集中，如此实现递归调用。如果输入列表(input list,用于记录个体的全部输入)过长，那么将停止递归。

评估

每个个体都是一个Lambda推演中的表示expression，评估的过程则是将数据集应用到这个表示中：
\[(λx.E)(dataset) → E[dataset/x]\]

遗传操作

进化的过程PolyGP中使用了遗传算法的稳态机制(steady-state)，在稳态机制中交叉后产生的新个体将会直接替代原有种群中适应度最低的个体。PolyGP的作者认为稳态机制可以保证产生的个体可以直接加入到现有种群中进行遗传操作加快进化，而不至于等到下一代。

交叉

PolyGP的交叉依赖于个体科里化的表达。
在较低端树叶层级的交叉与点突变作用类似，相当于随机搜索。因此为了产生更大规模的遗传物质交换，系统限制了交叉只能出现在application的节点，即任何可以被抽象为<expression1><expression2>的节点上。
PolyGP的交叉仍然是一种类保护的交叉，其具体做法如下：
第一个交叉点可以在亲本的application节点上任意选择，选择好后返回这个节点对应的深度和返回类型。第二个交叉点需要按照第一个交叉点的深度和返回类型选择与之相符合的节点：

• 深度信息是为了防止交叉之后的子树超过最大深度
  
• 第二个交叉点下子树返回的返回类型需要与第一个交叉点下子树的返回类型合一，如此保证新生成的树的合法性。

同时，在交叉的过程中，第二交叉点下子树的存在的临时类型变量会根据第一个交叉点所要求的返回类型进行实例化。
需要注意的是，PolyGP中的交叉操作是单后代交叉，最终产生的后代是由第一亲本决定的。

交叉的例子

现在有两个亲本：
\(P1\)为上个例子中的结果：
\[((IF-ELSE^{bool→[G2]→[G2]→[G2]} 【×】\underline{(NULL^{bool→[T1]} NIL^{[T2]})^{T1})^{[G2]→[G2]→[G2]}} (HEAD^{[[G2]]→[G2]} NIL^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\] \(P2\)的写法如下：
\[((IF-ELSE^{bool→T1→T1→T1}【×】\underline{(NULL^{[G1]→bool}L^{[G1]})^{bool})^{[T1]→[T1]→[T1]}}(HEAD^{[T1]→T1}NIL^{[T1]})^{[T1]→[T1]}(HEAD^{[T1]→T1}NIL^{[T1]})^{T1})^{T1}\] 【×】为交叉点，下划线的部分是交叉的部分。
交叉的结果为：
\[((IF-ELSE^{bool→[G2]→[G2]→[G2]} \overline{(NULL^{[G1]→bool} L^{[G1]})^{bool}})^{[G2]→[G2]→[G2]} (HEAD^{[[G2]]→[G2]} NIL^{[[G2]]})^{[G2]→[G2]} ((MAP^{(G1→G2)→[G1]→[G2]} F^{(G1→G2)})^{[G1]→[G2]})L^{[G2]})^{[G2]}\] 上划线的位置为交叉的部分。

下面的动画展示了这一过程：

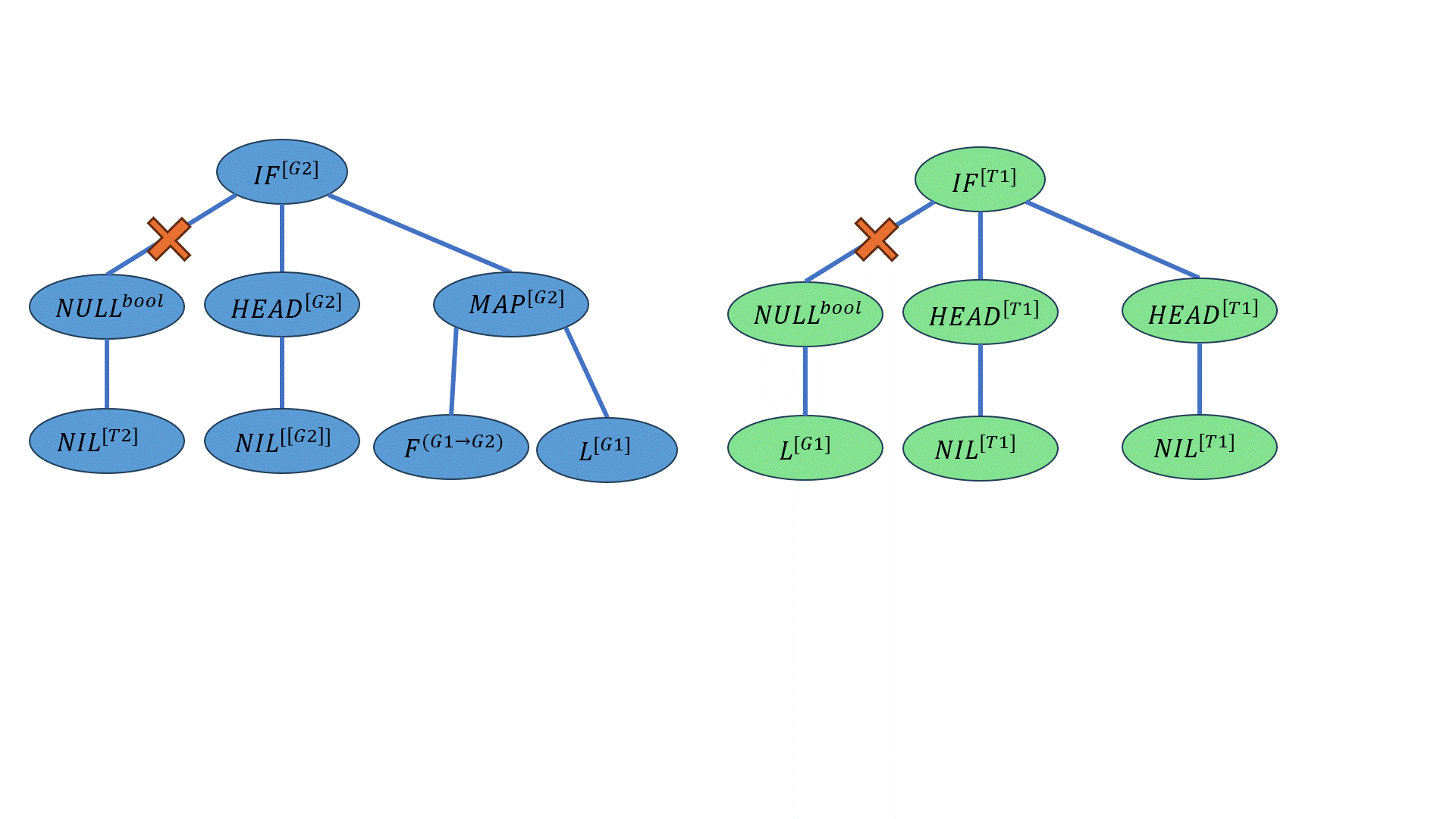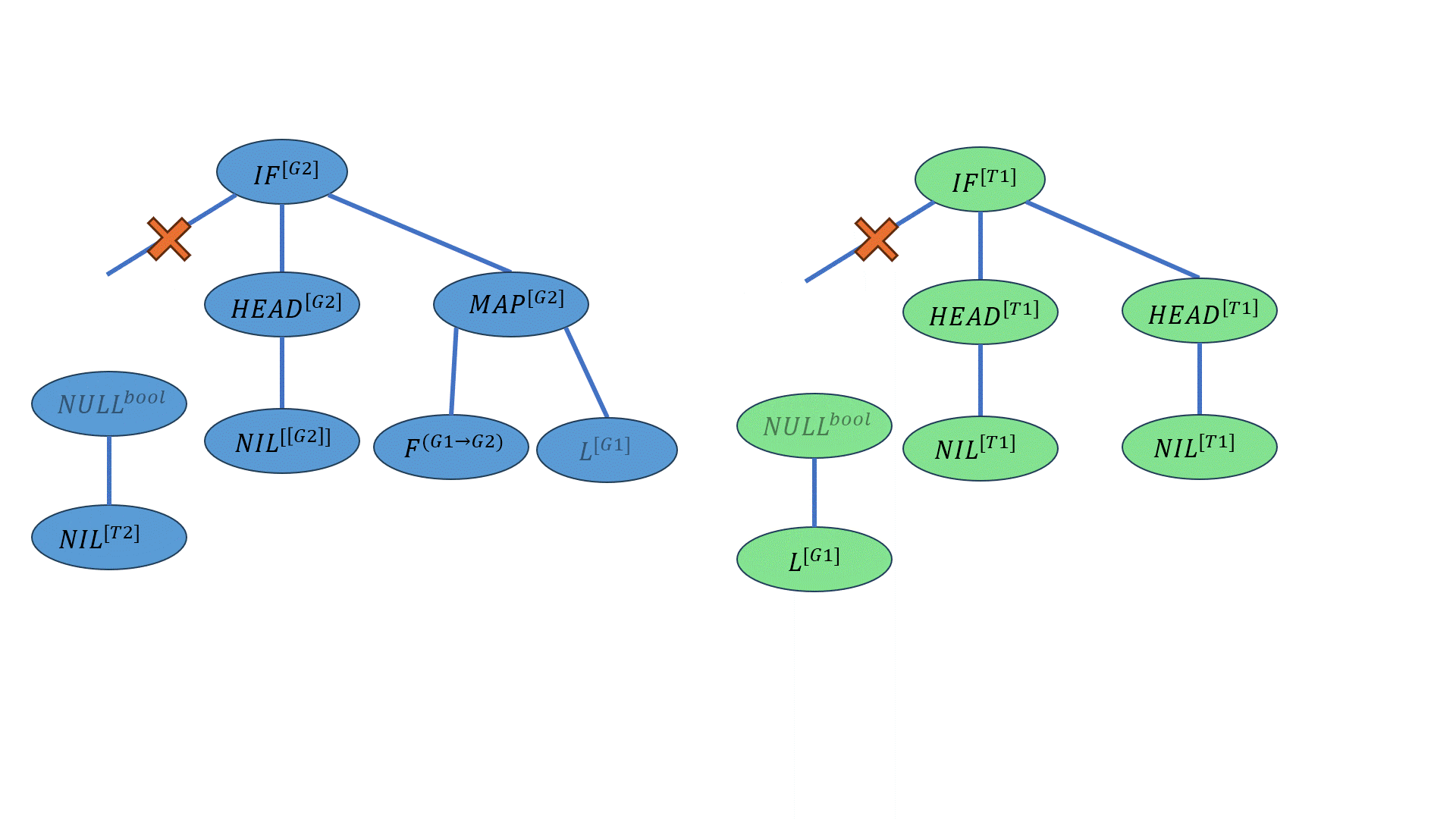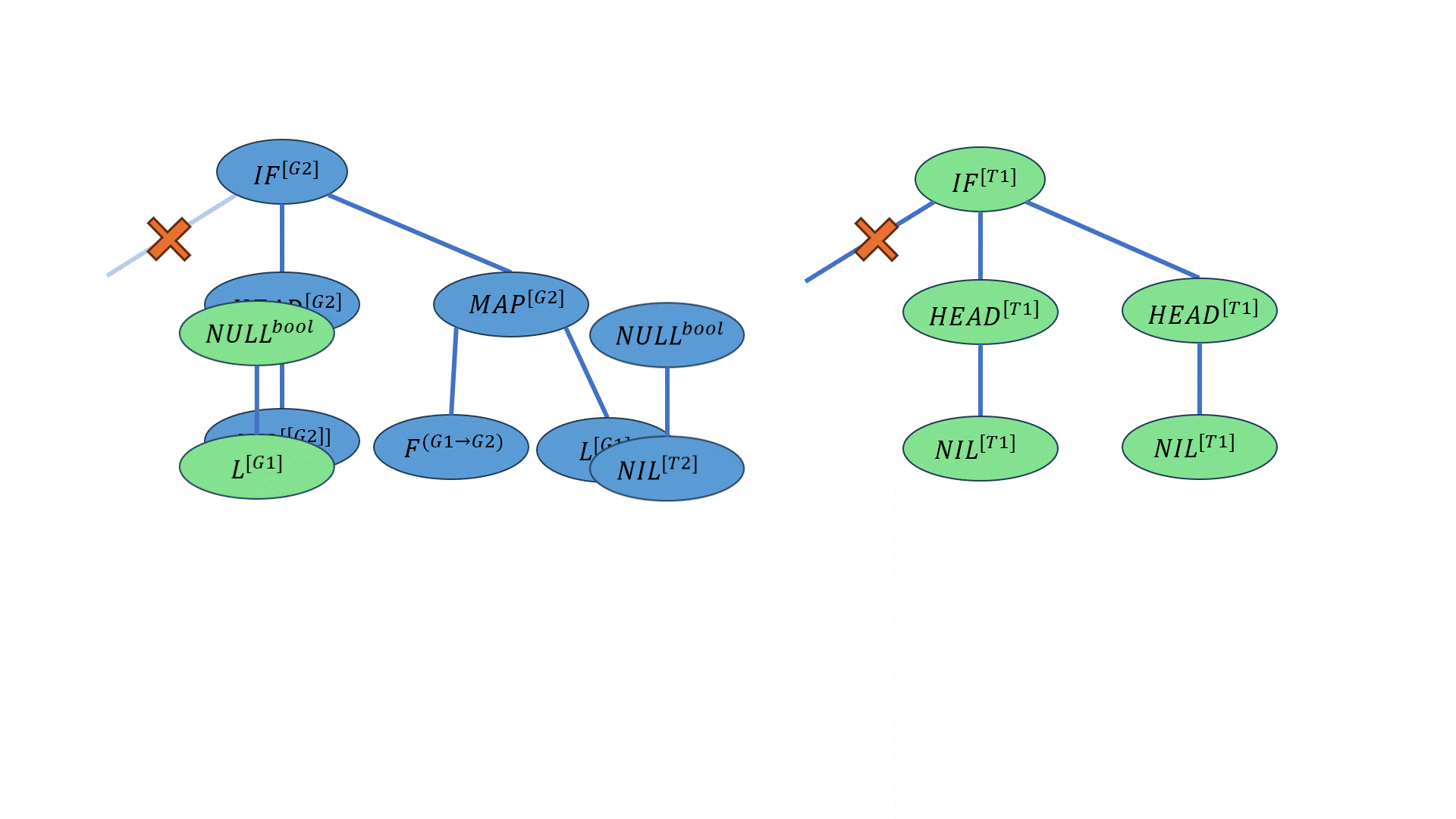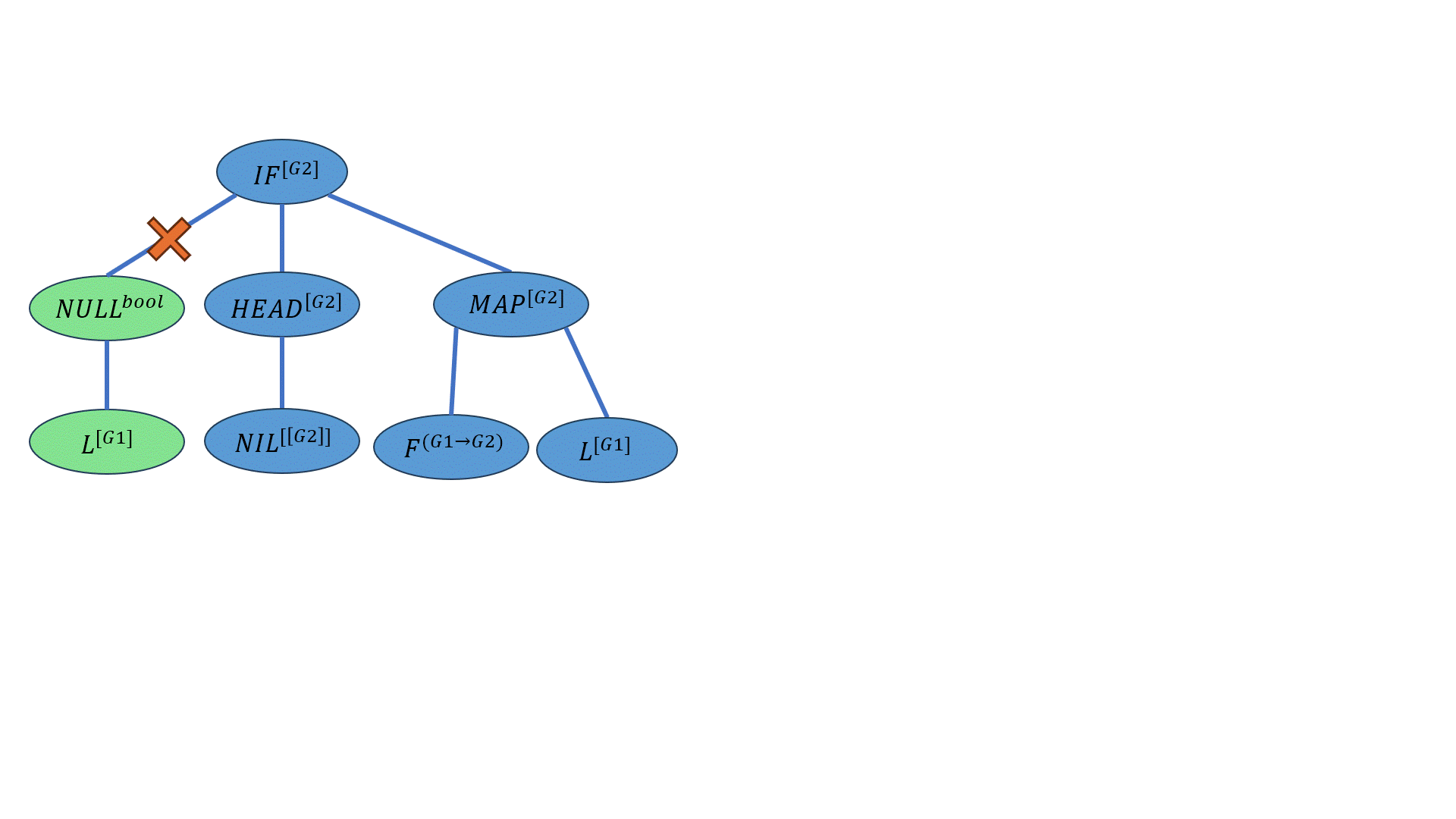
突变

突变使用的是点突变：随机在个体上选择一个结点并返回深度和类型，然后将该点下方的子树替换为一个随机生成的子树。子树的随机生成方式同个体的随机生成方式，并且需要满足要求的深度和返回类型。

1. Tina Yu, Chris Clack., PolyGP: A Polymorphic Genetic Programming System in Haskell, 1998. ↩︎
2. David J. Montana, Strongly Typed Genetic Programming, 1995. ↩︎
3. Robinson, J. A. (1965). A machine-oriented logic based on the resolution principle. Journal of the ACM (JACM), 12(1), 23-41. ↩︎
4. Rual Rojas, A Tutorial Introduction to the Lambda Calculus, 2015. ↩︎
5. Chris Clack, Tina Yu, Performance Enhanced Genetic Programming, 1995. ↩︎
6. R.Milner. A Theory of Type Polymorphism in Programming. Journal of Computer and System Sciences, 1978. ↩︎