同源交叉的模式定理

Riccardo Poli et al,. Exact Schema Thoery and Markov Chain Models for Genetic Programming and Variable-length Genetic Algorithms with Homologous Crossover, Genetic Programming and Evolvable Machines, 2004.

在这篇论文当中，Poli等人对GP构建了两种不同的Schema Thoery 模型： Exact Schema Theory和Markov模型，这两种模型分别从不同的视角描述了一个Schema在进化过程中的动态演进过程。但是这两个模型的实质上是对同一个GP的进化过程进行的不同视角的描述。

定义

进化计算的动态性研究中，不同的学者对于基本术语的理解和定义不太相同。在正式介绍这两种不同的概率模型之前，现在对这些术语在本文中的意义进行规范。

树的坐标表示

为了更好的公式化一颗树中节点的位置，定义树存在于一个以根节点的位置作为原点的坐标系当中，这个坐标系的表示如下图所示：

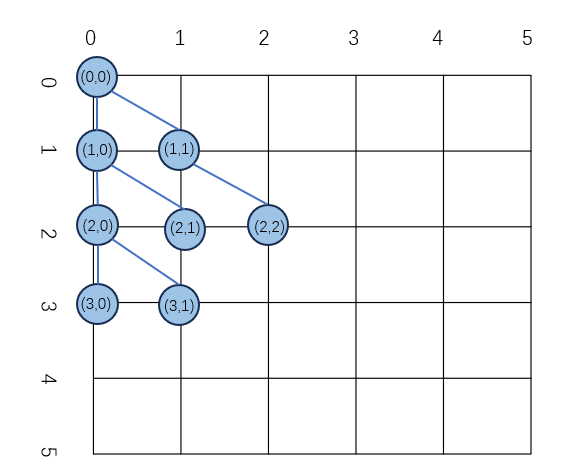
模式

模式(schema)是一组具有共同语法特征的个体。(a set of points of the search sapace sharing some syntactic feature)。模式带有don't care符号\(=\)，\(=\)可以是任何的端点或者函数。模式是对一群个体的拓扑结构的归纳，一组模式中的所有个体的结构在不是“=”的节点上是相同的。

对于任何一个模式\(H\)，Holland的模式定理可以简化为这个模式的在下一代中期望的个体数目是这一代的种群大小\(M\)与一个和\(H\)、\(t\)相关的系数的乘积之和：
\[E[m(H,t+1)]=Mα(H,t) \tag{0-1}\] \(α(H,t)\)称为schema \(H\)的转换概率，表示第\(t\)代个体\(H\)经过选择和繁殖后留存到下一代的概率。

如果考虑交叉过程，这个转换概率应当分为发生交叉和不发生交叉两部分：
\[α(H,t) = (1-p_c)p(H,t)+p_cα_c(H,t) \tag{0-2}\] 其中\(α_c(H,t)\)为发生交叉的转换概率。

最大相似区域

最大相似区域(common parts/common regions)是指两个亲本从根节点开始的最大的拓扑结构重叠区域。

理论1：

如果交叉发生在最大相似区域中，整个schema的多样性将不会发生任何变化。
下图展示了最大相似区域的定义以及这个理论在单点交叉上成立的图示：

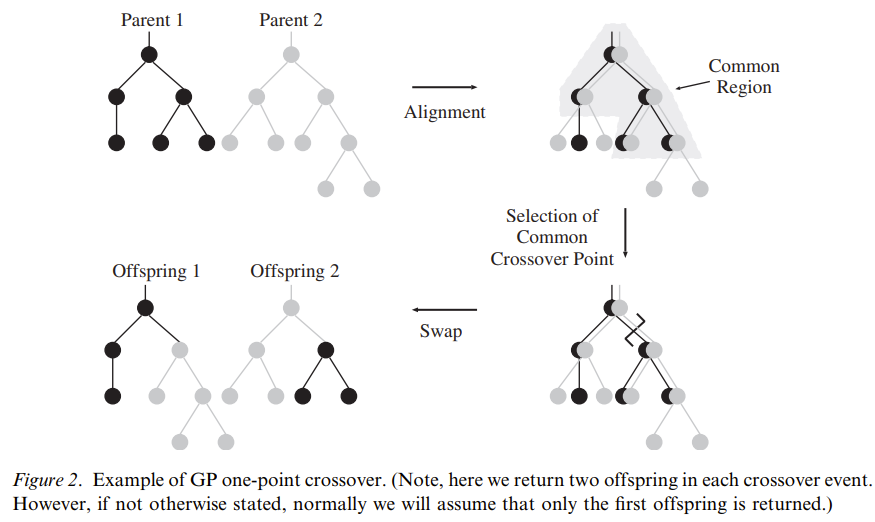
因此，要想保证schema不会受到破坏，两个亲本的交叉应当发生在它们的最大相似区域中。

最大相似区域的数学定义

首先定义函数\(A(d,i,h)\)用于返回树\(h\)在坐标\((d,i)\)处的节点需要的参数个数(arity)，如果\(h\)在\((d,i)\)处没有节点，则返回-1.
现在定义一个函数common region membership function \(𝒞(d,i,h_1,h_2)\)用于检查坐标\((d,i)\)是否属于\(h_1,h_2\)的common region，满足如下条件则该节点属于\(h_1,h_2\)的common region：

1. 该节点是一个根节点
2. \(h_1\)和\(h_2\)上该节点对应的父节点的区域属于common region 该节点在\(h_1\)和\(h_2\)的父节点的参数数量相同（子树的分支数量相同）

\[𝒞(d,i,h_1,h_2)=\begin{cases} true, \text{ if}(d,i)=\text{root} &\\ true, \text{ if} [A(parent(d,i),h_1)=A(parent(d,i),h_2)≠0] AND &\\ [\text{ }(d,i,h_1)≥0,A(d,i,h_2)≥0] AND [ 𝒞(parent(d,i),h_1,h_2)=true] \\ false, otherwise \end{cases}\]

根据这个式子，可以对common region定义为所有满足\(𝒞(d,i,h_1,h_2)=true\)的点的集合：
\[C(h_1,h_2)=\{(d,i)|𝒞(d,i,h_1,h_2)=true\}\]

shape

shape指一个schema中所有的节点都被\(=\)替代，它代表只关心schema的结构，不关心每个节点的具体内容。

超模式

超模式(hyper schema)是对某个模式的进一步抽象，和模式不同的是，超模式允许对子树结构进行抽象，即忽略某个节点的子树结构，这个节点下的子树结构用don't care，\(\#\)替代。\(\#\)可以是任何的子树结构。
从另一个角度理解，超模式是符合某个schema的所有个体的集合。超模式可以用于表达产生一个schema的两个亲本个体所必须具备的属性。

个人认为，需要Hyper schema的原因是为了进一步的描述building blocks在个体当中的相对位置关系。

Building blocks

这篇论文中没有对building blocks给出非常详细的定义，但是通过公式可以判断，作者认为building blocks是schema的进一步抽象，并且组成schema。具体的，作者认为schema按照一定的方式划分为两半并且抽象得到的结果称为building blocks。交叉的亲本应该各持有一部分这两部分building blocks。

Schema的视角 - Exact Schema Thoery

单点交叉的模拟

upper build blocks和lower building blocks

作者认为，单点交叉的building blocks为schema在交叉点处划分的上下两部分的抽象，分为upper building blocks和lower building blocks， 亲本应当各持有这两个building blocks。
这两个building blocks具体的划分如下：

• upper building blocks
  记为\(U(H,i)\)，通过将schema \(H\)上对应交叉点\(i\)下方的所有子树抽象为\(\#\)得到。换言之即不关心交叉点下方的结构。

• lower building blocks
  记为\(L(H,i)\)，抽象方法如下：

  • schema \(H\)上对应交叉点\(i\)到根节点路线上的所有节点替换为\(=\)，如果这些被替换为\(=\)的节点存在子节点，那么这些子节点将被替换为\(\#\). 换言之不关心交叉点上方的结构（但是需要保持schema的拓扑连结）。

两种划分方法如下图所示：

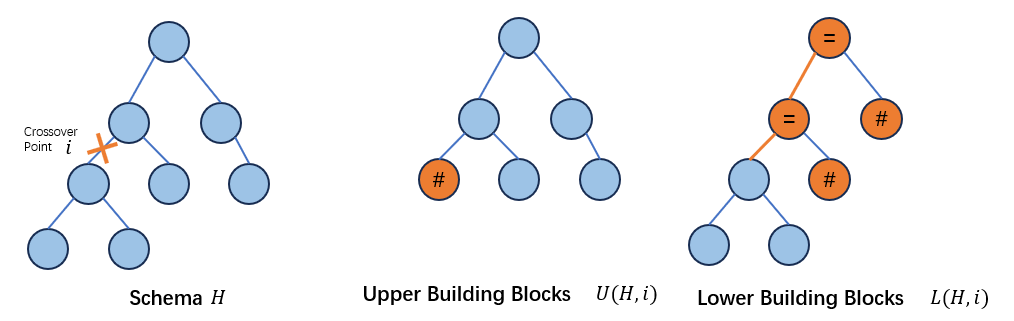
因此，如果两个亲本\(h_1,h_2\)交叉后的个体想要在schema \(H\)中，那么对所有可能发生的交叉点\(i\)，它们的两个亲本所属的shape\(G_k\)和\(G_j\)需要各自持有schema \(H\)的upper building blocks\(U(H,i)\)和lower building blocks\(L(H,i)\)。并且，根据理论1，只有当交叉点在\(G_k\)和\(G_j\)（或者说\(h_1,h_2\)）的common region时，交换后才会生成/保留schema的拓扑结构。
因此，式(0-2)中的\(α_c(H,t)\)进一步表示为：
\[α_c(H,t)=∑_{k,l}\frac{1}{|C(G_k,G_l)|}×∑_{i∈C(G_k,G_l)}p(U(H,i)∩G_k,t)p(L(H,i)∩G_l,t) \tag{1-0}\] 其中\(|C(G_k,G_l)|\)表示\(G_k\)和\(G_l\)的common region的节点总数;\(∩\)表示两个树的共同部分的截取。

同源交叉的模拟

接下来，作者试图将Exact Schema Thoery 拓展到同源交叉。所谓同源交叉(homologous crossover)即两个亲本个体发生的点对点的交叉。在遗传算法中，同源交叉是通过模板(mask)来实现的。简单来说，遗传算法中设计好一个二进制的mask，用0代表来自其中一个亲本\(h_1\)的比特片段，用1代表来自另一个亲本\(h_2\)的比特片段，后代根据这个模板中对应比特的来源信息从两个亲本中填入比特：

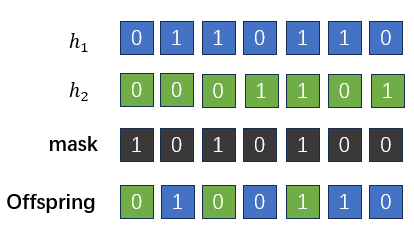
在本文中，作者借用了遗传算法中使用模板的方法，任何在common region中进行的交叉都可以用模板进行表示。因此，模板的shape应当与common region的shape相同。
同样地，结合树的坐标表示，在common region中的任何部分都可以用0和1来表示后代中每个节点与亲本的来源关系。

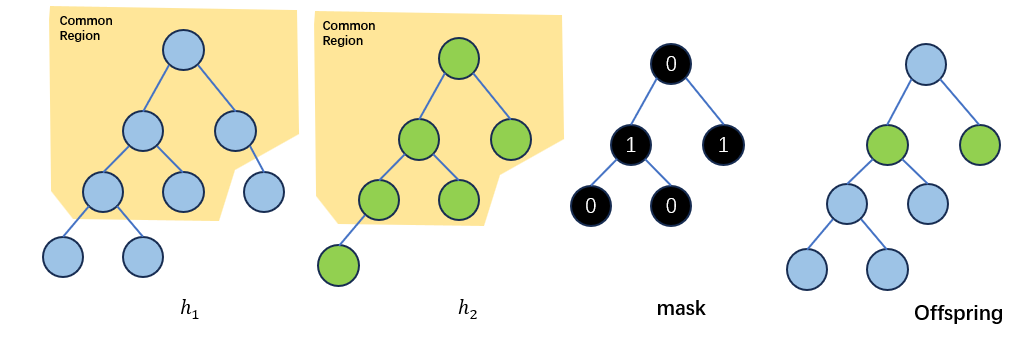
定义如果\(i\)代表\(h_1\)和\(h_2\)的一个模板，\(\overline{i}\)则表示与\(i\)中的0/1完全相反的一个模板。
并且定义\(χ_{C(h_1,h_2)}\)表示\(h_1\)和\(h_2\)的common region的所有可能的模板的集合，\(χ_{C(h_1,h_2)}\)中应当有\(2^{|C(h_1,h_2)|}\)个元素，即\(2^{|C(h_1,h_2)|}\)种不同的可能模板。
进化过程中交叉所使用的模板是有概率进行选择的，记\(p_i^C\)表示common region \(C\)中的第\(i\)个模板被选择用于交叉的概率，那么集合\(\{p_i^c|∀c\}\)则表示了遗传编程中所使用的交叉算子的特性。不同的交叉算子中\(p_i^c\)的概率不尽相同。

building block的提取

和单点交叉一样，接下来当提取出两个亲本应当各自持有的schema的一部分，称为building blocks。但是同源交叉下提取并抽象这两部分要比单点交叉更加复杂。
定义building blocks的提取函数\(Γ(H,i)\)，它可以对schema \(H\)根据模板\(i\)提取出标记为1的亲本所持有的building blocks。其提取方法如下：
对于如果在\(H\)上的某个非最底层节点(none-leaf node)被\(i\)标记为0，那么它将被“=”替代，如果一个底层节点(leaf node)被\(i\)标记为0，那么它将被"#"替代：

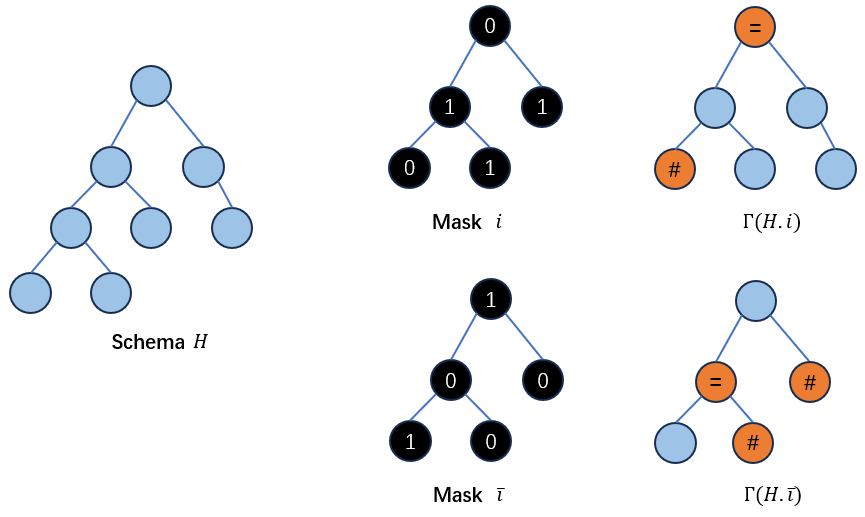
那么相应地，\(Γ(H,\overline{i})\)可以根据模板\(i\)提取出标记为0的亲本所持有的building blocks。

此处对于“持有”的理解是，building blocks本质上也是对个体特征的描述，因此一个building block也是满足这个特征的所有个体的集合。因此，一个个体“持有”某个building block可以理解为该个体是这个building block所代表集合的成员：\(h_1 ∈ Γ(H,i)\)

理论2：

对于一个schema \(H\)，持有building block\(Γ(H,i)\)的个体与另一个持有building block\(Γ(H,\overline{i})\)的个的交叉的后代一定属于schema \(H\)。反之，产生后代属于\(H\)的两个亲本一定各自持有building block\(Γ(H,i)\)和\(Γ(H,\overline{i})\)。

if one crossover using crossover mask \(i\) any individual in \(Γ(H,i)≠∅\) with any individual in \(Γ(H,\overline{i})≠∅\), the resulting offspring is always an instance of \(H\). Coversely, if two individuals cross using mask \(i\) to form an element of \(H\), then one of them must have come from \(Γ(H,\overline{i})\) and the other from \(Γ(H,\overline{i})\).

同源交叉下 Exact Schema Thoery的完整推导

设\(p_i(h_1,h_2,i,t)\)表示个体\(h_1\)和\(h_2\)以及交叉模板\(i\)在第\(t\)代被选中的概率；\(g(h_1,h_2,H,i)\)为\(h_1\)和\(h_2\)按照模板\(i\)交叉后产生属于schema \(H\)的个体的概率。
那么有:
\[α_c(H,t)=∑_{h_1}∑_{h_2}∑_ip(h_1,h_2,i,t)g(h_1,h_2,H,i) \tag{1-1}\] 先看\(p_i(h_1,h_2,i,t)\)，它可以理解为“选择模板\(i\)”(事件\(A\))和“选择个体\(h_1\)和\(h_2\)(事件\(B\))”两件事情同时发生的概率，在贝叶斯公式中对应\(P(AB)\). 根据贝叶斯公式\(P(AB)=P(A|B)P(B)\)，其中\(P(B)=p(h_1,t)p(h_2,t)\)，分别代表个体\(h_1\)和\(h_2\)在第\(t\)代时被选中的概率，那么式子\((1-1)\)可以改写为：
\[α_c(H,t)=∑_{h_1}∑_{h_2}∑_ip(h_1,t)p(h_2,t)p(i|h_1,h_2)g(h_1,h_2,H,i) \tag{1-2}\] 对\(p(i|h_1,h_2)\)，它指的是当\(h_1\)和\(h_2\)被选中时，模板\(i\)被选中的概率（在\(B\)的条件下发生\(A\)的概率）。交叉模板\(i\)应当与\(h_1\)和\(h_2\)的common region的形状相同，被选中需要满足两个条件：1. \(i\)属于\(h_1\)和\(h_2\)的common regions的模板 2. 在这些模板中，\(i\)需要被选中。 因此有：
\[p(i|h_1,h_2)=δ(i∈χ(h_1,h_2))p_i^{C(h_1,h_2)}\] 其中\(δ(.)\)是一个判断函数，当满足其中的条件时其值为1，否则为0。\(∑δ(.)\)表示在可能的遍历过程中这个条件被满足了多少次。
那么，
\[\begin{aligned} α_c(H,t)=&∑_{h_1}∑_{h_2}∑_ip(h_1,t)p(h_2,t)δ(i∈χ(h_1,h_2))p_i^{C(h_1,h_2)}g(h_1,h_2,H,i)\\ =&∑_{h_1}∑_{h_2}∑_{i∈χ(h_1,h_2)}p(h_1,t)p(h_2,t)p_i^{C(h_1,h_2)}g(h_1,h_2,H,i) \end{aligned} \tag{1-3}\] 根据乘法分配律，现在将与模板\(i\)相关的内容归结到一起：
\[α_c(H,t)=∑_{h_1}∑_{h_2}p(h_1,t)p(h_2,t)∑_{i∈χ(h_1,h_2)}p_i^{C(h_1,h_2)}g(h_1,h_2,H,i) \tag{1-4}\] 再来看\(g(h_1,h_2,H,i)\)，要想\(h_1\)和\(h_2\)按照模板\(i\)交叉后产生属于schema \(H\)的个体，那么根据理论2，当\(h_1\)和\(h_2\)各自持有building block\(Γ(H,i)\)和\(Γ(H,\overline{i})\)时，此时一定可以产生属于schema \(H\)的个体（概率为1），否则一定不能产生属于schema \(H\)的个体（概率为0） 有：
\[g(h_1,h_2,H,i)=δ(h_1∈Γ(H,i))δ(h_2∈Γ(H,\overline{i}))\] 乘积在此的作用相当于逻辑中的\(AND\)，表示两种情况同时发生时才可以发生。
那么：
\[\begin{aligned} α_c(H,t)=&∑_{h_1}∑_{h_2}p(h_1,t)p(h_2,t)\\ &×∑_{i∈χ(h_1,h_2)}p_i^{C(h_1,h_2)}δ(h_1∈Γ(H,i))δ(h_2∈Γ(H,\overline{i})) \end{aligned} \tag{1-5}\] \(h_1\)和\(h_2\)一定属于某些shape，有\(∑_jδ(h_1∈G_j)=1\)，那么向式\((1-5)\)添加关于shape的信息对式子本身不会有任何影响：
\[\begin{aligned} α_c(H,t)=&∑_{h_1}∑_{h_2}∑_j∑_kp(h_1,t)p(h_2,t)\\ &×∑_{i∈χ(h_1,h_2)}p_i^{C(h_1,h_2)}δ(h_1∈Γ(H,i))δ(h_1∈G_j)δ(h_2∈Γ(H,\overline{i}))δ(h_2∈G_k)\\ =&∑_{h_1∈G_j}∑_{h_2∈G_k}p(h_1,t)p(h_2,t)\\ &×∑_{i∈χ(h_1,h_2)}p_i^{C(h_1,h_2)}δ(h_1∈Γ(H,i))δ(h_2∈Γ(H,\overline{i})) \end{aligned} \tag{1-6}\] 因为\(h_1∈G_j\),\(h_2∈G_k\)，它们的common region应该是一样的：\(C(h_1,h_2)=h(G_j,G_k)\)，那么：
\[\begin{aligned} α_c(H,t)=&∑_j∑_k∑_{h_1∈G_j}∑_{h_2∈G_k}p(h_1,t)p(h_2,t)\\ &×∑_{i∈χ(G_j,G_k)}p_i^{C(G_j,G_k)}δ(h_1∈Γ(H,i))δ(h_2∈Γ(H,\overline{i})) \end{aligned} \tag{1-7}\] 将这个式子重新整理，有：
\[\begin{aligned} α_c(H,t)=&∑_j∑_k∑_{i∈χ(G_j,G_k)}p_i^{C(G_j,G_k)}∑_{h_1∈G_j}p(h_1,t)δ(h_1∈Γ(H,i))\\ &×∑_{h_2∈G_k}p(h_2,t)δ(h_2∈Γ(H,\overline{i})) \end{aligned} \tag{1-8}\] 其中\(∑_{h_1∈G_j}p(h_1,t)=p(G_j,t)\)，\(∑_{h_2∈G_k}p(h_2,t)=p(G_k,t)\)，有\(∑_{h_1∈G_j}p(h_1,t)δ(h_1∈Γ(H,i))=p(Γ(H,i)∩G_j,t)\),\(∑_{h_2∈G_k}p(h_2,t)δ(h_2∈Γ(H,i))=p(Γ(H,\overline{i})∩G_k,t)\)
那么，
\[α_c(H,t)=∑_j∑_k∑_{i∈χ(G_j,G_k)}p_i^{C(G_j,G_k)}p(Γ(H,i)∩G_j,t)p(Γ(H,\overline{i})∩G_k,t) \tag{1-9}\] 带入式\((0-2)\)中：
\[\begin{aligned} α(H,t) = & (1-p_c)p(H,t)\\ &+p_c[∑_j∑_k∑_{i∈χ(G_j,G_k)}p_i^{C(G_j,G_k)}p(Γ(H,i)∩G_j,t)p(Γ(H,\overline{i})∩G_k,t)] \end{aligned}\] 这是最终的Exact Schema Thoery.

此处如果可以证明：
\[p(Γ(H,o)∩G_j,t)p(Γ(H,\overline{o})∩G_k,t)\xlongequal{\ce{?}}∑_x∑_y...∑_zp(Γ(H,x)∩G_j,t)p(Γ(H,\overline{x})∩G_k,t)p(Γ(H,y)∩G_j,t)p(Γ(H,\overline{y})∩G_k,t)...p(Γ(H,z)∩G_j,t)p(Γ(H,\overline{z})∩G_k,t)\]

其中\(Γ(H,x),Γ(H,y),...,Γ(H,z)∈Γ(H,o)\)且模板\(x,y,...,z\)共同组成模板\(o\) 那么某个同源交叉的building block其实可以看做是若干个单点交叉的building block\(U(H,i)\)和\(L(H,i)\)的组成，上述公式可证同源交叉实际上是多个单点交叉的合集。
事实上是，这个等式并不成立。下面的一个小实验说明的这一点：

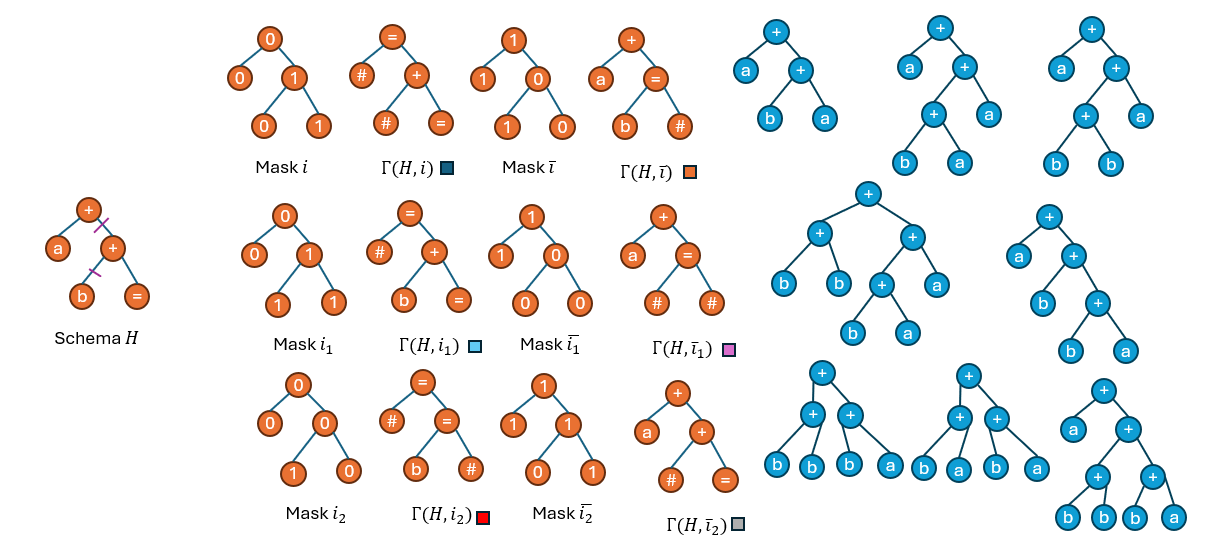
如上图所示，mask \(i\)被拆分成了两个单点交叉的mask \(i_1\)和\(i_2\)，分别得到它们以及取反后的building blocks。蓝色的部分为现有种群。
然后观察现有种群中的个体分别属于哪些hyper schema（以下图中每个个体下方的色块表示），并统计每一个hyper schema的采样率：

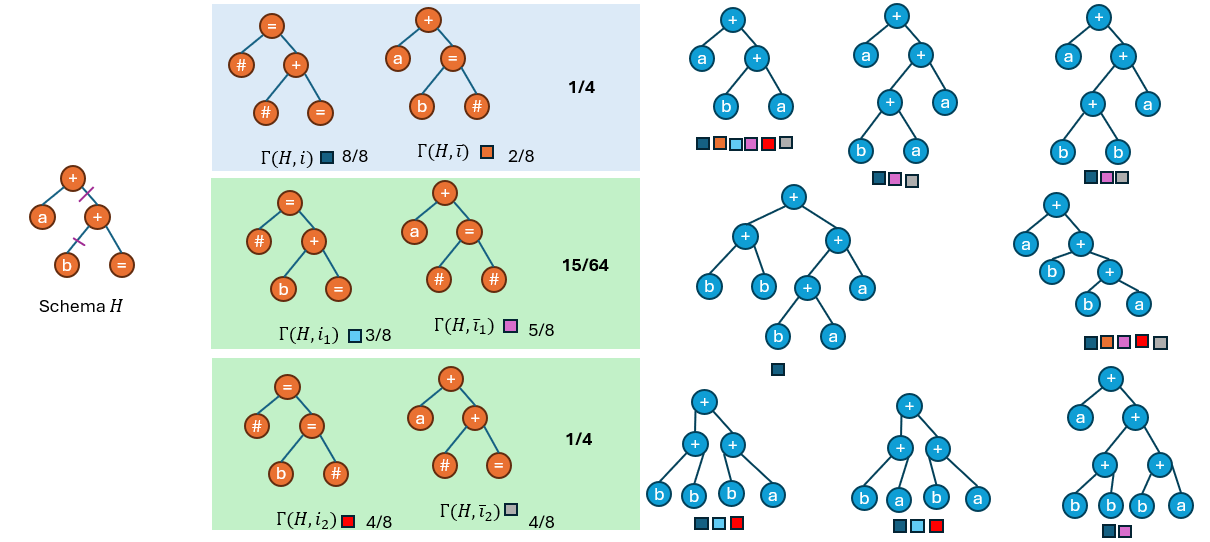
可以发现，\(Γ(H,i)\)的采样率为1，\(Γ(H,\overline{i})\)的采样率为2/8;\(Γ(H,i_1)\)的采样率为3/8，\(Γ(H,\overline{i_1})\)的采样率为5/8;
\(Γ(H,i_2)\)的采样率为4/8，\(Γ(H,\overline{i_2})\)的采样率为4/8.
上述等式并不成立。
因此，同源交叉并不是多个单点交叉的合集。
也可以见Poli, Riccardo & Langdon, W.. (2001). On the Search Properties of Different Crossover Operators in Genetic Programming. 中单点交叉和均匀交叉的信息交换能力是不同的。交叉算子的建模和比较

收敛性分析

如果刚开始种群的多样性足够大，那么一开始种群中的conmmon region的面积非常小，此时\(i\)的大小非常小，\(Γ(H,i)\)和\(Γ(H,\overline{i})\)的抽象程度都很高，因此\(p(Γ(H,i)∩G_j,t)p(Γ(H,\overline{i})∩G_k,t)\)比较大。

关于最大值的推论，最大的情况发生（实际是不可能发生）在：\(i\)不进行任何抽象(也就是说种群中的每个个体都不相同)，也就是\(i\)和\(\overline{i}\)中只含有一个结点。这种情况比较难推理，遂放缩到\(i\)和\(\overline{i}\)中不含有任何结点的情况，此时有\(p(Γ(H,i)∩G_j,t)=p(G_j)\)，\(p(Γ(H,\overline{i})∩G_k,t)=p(G_k)\)，有\(\sum_k\sum_jp(G_j)p(G_k)=1\)，带入得到\(\hat{α}_c(H,t)=p_c\).
也就是说：\(α_c<p_c\).

随着进化的进行，conmmon region的面积增大，此时\(Γ(H,i)\)和\(Γ(H,\overline{i})\)的抽象程度降低，\(p(Γ(H,i)∩G_j,t)p(Γ(H,\overline{i})∩G_k,t)\)的概率逐渐减小，最终\(\sum_k\sum_jp(Γ(H,i)∩G_j,t)p(Γ(H,\overline{i})∩G_k,t)\)收敛到\(p(H,t)\).
此时有：\(α(H,t)=(1-p_c)p(H,t)+p_cp(H,t)=p(H,t)\)，交叉对进化不产生任何作用。

个体的视角 - Markov Model

Vose在遗传算法中的Schema Theory

Vose通过马尔科夫链中的一步转移概率矩阵对遗传算法的动态性进行了描述，下面将简述Vose的Schema Thoery.
设\(Ω\)代表所有长度为\(l\)的个体组成的集合，\(r=|Ω|=2^l\). 设\(Pop\)为一个种群，其种群大小为\(n=|Pop|\).根据重复组合定理，从\(r\)个个体中可以重复的选择\(n\)个个体构成种群的所有可能的方式数量记为\(N\),\(N=C_{n+r-1}^r\)

现在定义一个大小为\(r×N\)的接续矩阵(incidence matrix)\(Z\)，\(Z\)的第\(i\)列代表第\(i\)个可能的种群\(Pop_i\):\(Φ_i=[z_{0,i},z_{1,i}...,z_{r-1,i}]^T\)，其中的一个元素\(z_{y,i}\)代表\(Pop_i\)中的第\(y\)个个体的出现频数。
根据上述的定义，为\(Ω\)中的每一个个体建立马尔科夫链当中的一步概率转移矩阵\(Q\)，其中每一个元素\(Q_{ij}\)代表从种群\(Pop_i\)转移到\(Pop_j\)的概率。
如果记\(p_i(y)\)表示\(Pop_i\)中的个体在下一代中变成个体\(y\)的概率，那么\(Q_{ij}\)就应当是\(p_i(y)\)的概率的乘积（因为\(Pop_i\)中的每一个元素都需要转移到\(Pop_j\)中，这是且的关系）。\(Pop_i\)中每一个个体都可以转移成\(Pop_j\)中的任意一个个体，但是它们之中有一些个体是相同的，因此将每一个个体视为是一个集合，采用多重集合的排列公式计算所有的可能性。所有可能的组合数量为： \[\frac{n!}{(z_{0,j}!z_{1,j}!z_{2,j}!…z_{r-1,j}!)}\] 那么，
\[Q_{i,j}=\frac{n!}{(z_{0,j}!z_{1,j}!z_{2,j}!…z_{r-1,j}!)}∏_{y=0}^{r-1}(p_i(y))^{z_{y,j}} \tag{2-0}\]

多重集合排列公式的数学证明

多重集合排列公式：
设\(S\)是多重集合，它有\(k\)种不同类型的对象，每一种类型的有限重复数是\(n_1,n_2,n_3,…,n_k\)。设\(S\)的大小为\(n=n_1+n_2+n_3+…n_k\)。则\(S\)的\(n\)排列数目为: \[\frac{n!}{(n_1!n_2!n_3!…n_k!)}\] 证明： 先从\(S\)中选出\(n_1\)个位置放\(a_1\)，有\(C_n^{n_1}\)种放法，再选出\(n_2\)个位置放\(a_2\)，有\(C_{n-n_1}^{n_2}\)种放法，以此类推：
由乘法原理得：
\(S\)的排列个数为\(C_n^{n_1}C_{n-n_1}^{n_2}C_{n-n_1-n_2}^{n_3}…C_{n-n_1-n_2-…-n_{k-1}}^{n_k}\).
带入组合计算公式，有：
\[ \frac{n}{n!(n-n_1)!}\frac{(n-n_1)!}{n_2!(n-n_1-n_2)!}...\frac{(n-n_1-n_2-...-n_{k-1})!}{n_k!(n-n_1-n_2-...-n_k)!}\] 去公因式可得证。

接下来考虑如何求\(p_i(y)\)，要想产生后代\(y\)，那么需要选择合适的亲本进行交叉，因此\(p_i(y)\)由三部分组成：选择亲本个体\(m\)的概率\(s_{m,i}\)、选择亲本\(n\)的概率\(s_{n,i}\)以及交叉在\(m,n\)上产生\(y\)的概率\(rec_{m,n}(y)\)：
\[p_i(y)=∑_{m,n}^{r-1}s_{m,i}s_{n,i}rec_{m,n}(y) \tag{2-1}\]

• 选择的表示 亲本个体被选择的概率为该个体在现有种群中出现的频率与其归一化的fitness的乘积：
  \[s_{m,i}=\frac{z_{m,i}f(m)}{∑_{j=0}^{r-1}z_{j,i}f(j)}\tag{2-2}\] 将式子(2-2)进行矩阵化，令\(x\)是一个种群的接续向量，其内部的元素为这个种群中的所有个体的出现频数；设\(f\)是一个含有该种群所有个体对应fitness的向量，对现有种群\(x\)的适应度比例选择表示为：
  \[ℱ(x)=\frac{diag(f)x}{f^Tx} \tag{2-3}\] 其中\(diag(f)\)是\(f\)的对角矩阵。
  

• 交叉的表示
  现在建立一个\(r×r\)的矩阵\(ℳ_y\)用于表示\(Ω\)空间中的每两个个体交叉产生\(y\)的概率，矩阵\(ℳ_y\)称为\(y\)的混淆矩阵(mixing matrix)，有：
  \[(ℳ_y)_{m,n}=rec_{m,n}(y)\] 如果不考虑对\(m、n∈i\)的选择，由\(i\)中的两个亲本\(m,n\)交叉产生\(y\)的概率与\(m、n∈x\)的出现频率有关，表示为：
  \[p_i(y)=Φ_i^Tℳ_yΦ_i \tag{2-4}\] \(m\)和\(n\)的选择不具有先后顺序:\(rec_{m,n}(y)=(ℳ_y)_{m,n}=rec_{n,m}(y)=(ℳ_y)_{n,m}\)，因此该公式的结构是对称性的：\(x^T[·]x\)
  现在考虑对\(m、n\)的选择，有：
  \[p_i(y)=ℱ(Φ_i)^Tℳ_yℱ(Φ_i) \tag{2-4}\]

  混淆向量ℳ的定义，在本文中跳过了使用这个定义

  定义一个范围更广的混淆向量\(ℳ\)，其表示了由种群\(x\)中的个体产生的下一代中每一个个体的存在频率，那么有：
  \[ℳ(x)=[x^Tℳ_0x,x^Tℳ_1x,x^Tℳ_2x,...,x^Tℳ_{r-1}x]\]

  将式(2-4)带入(2-0)中，有：
  \[\begin{aligned} Q_{i,j}&=\frac{n!}{(z_{0,j}!z_{1,j}!z_{2,j}!…z_{r-1,j}!)}∏_{y=0}^{r-1}[ℱ(Φ_i)^Tℳ_yℱ(Φ_i)]^{z_{y,j}}\\ \end{aligned} \tag{2-5}\]

遗传编程Homologous的Markov Model

在遗传算法中\(p_i(y)\)考虑讨论进行交叉和不进行交叉两部分。

• 如果不进行交叉，个体\(m\)转换为\(y\)的唯一可能是\(m\)就是\(y\)，此时\(n\)可以是任意一个个体：\(\sum_{n∈Ω}p(n,t)=1\)
  \[(1-p_c)\sum_{m∈Ω}δ(m=y)p(m,t)=(1-p_c)\sum_{m∈Ω}δ(m=y)p(m,t)\sum_{n∈Ω}p(n,t)\]
• 如果进行交叉，那么\(m,n\)产生\(y\)的概率将符合式\((1-8)\)，那么有：
  \[\begin{aligned} α(y,t) = & (1-p_c)p(y,t)\\ &+p_c[∑_j∑_k∑_{l∈χ(G_j,G_k)}p_l^{C(G_j,G_k)}p(Γ(y,l)∩G_j,t)p(Γ(y,\overline{l})∩G_k,t)] \end{aligned}\]

有：
\[\begin{aligned} p_i(y)=& (1-p_c)p(y,t)\\ &+p_c[∑_j∑_k∑_{l∈χ(G_j,G_k)}p_l^{C(G_j,G_k)}p(Γ(y,l)∩G_j,t)p(Γ(y,\overline{l})∩G_k,t)]\\ =&(1-p_c)\sum_{m∈Ω}δ(m=y)p(m,t)\sum_{n∈Ω}p(n,t)\\ &+p_c[∑_j∑_k∑_{l∈χ(G_j,G_k)}p_l^{C(G_j,G_k)}p(Γ(y,l)∩G_j,t)p(Γ(y,\overline{l})∩G_k,t)]\\ \end{aligned} \tag{3-1}\] 根据式子\((1-8)\),\((1-6)\):
\[\begin{aligned} p_i(y)=&∑_{m∈Ω}∑_{n∈Ω}p(m,t)p(n,t)×[(1-p_c)δ(m=y)\\ &+p_c∑_j∑_k∑_{l∈χ(m,n)}p_l^{C(m,n)}δ(m∈Γ(y,l)δ(m∈G_j)δ(n∈Γ(y,\overline{l}))δ(n∈G_k))]\\ =&∑_{m∈Ω}∑_{n∈Ω}p(m,t)p(n,t)×[(1-p_c)δ(m=y)\\ &+p_c∑_{l∈χ(m,n)}p_l^{C(m,n)}δ(m∈Γ(y,l)δ(n∈Γ(y,\overline{l})))] \end{aligned} \tag{3-2}\]

提取公因式\(∑_{m∈Ω}∑_{n∈Ω}p(m,t)p(n,t)=\sum_{m,n∈Ω}p(m,t)p(n,t)\)得到\((3-1)\)的变形:
\[p_i(y)=\sum_{m,n∈Ω}p(m,t)p(n,t)×[(1-p_c)δ(m=y)+p_c∑_{l∈χ(m,n)}p_l^{C(m,n)}δ(m∈Γ(y,l)δ(n∈Γ(y,\overline{l})))]\]

根据式\((2-1)\)，\(p_i(y)=∑_{m,n}^{r-1}s_{m,i}s_{n,i}rec_{m,n}(y)\)，有\(s_{m,i}=p(m,t)\)，\(s_{n,i}=p(n,t)\)，那么：
\[rec_{m,n}(y)=∑_{l∈χ(m,n)}p_l^{C(m,n)}δ(m∈Γ(y,l)δ(n∈Γ(y,\overline{l}))) \tag{3-3}\] 那么schema \(H\)的转换概率应该是schema \(H\)中的所有个体在后代中的存活概率之和：
\[α(H,t)=∑_{y∈H}p_i(y) \tag{3-4}\]

0/1树的Markov Model

Vose的遗传算法能够用概率转移矩阵表示的原因是因为遗传算法的个体表示是定长的二进制位串。遗传编程的搜索空间更加复杂，其对称性更难理解，看起来不会产生单一的混淆矩阵。因此为了探究遗传编程中的对称性，将遗传编程的树形结构进行最大程度上的简化：表现为0/1树： 在0/1树中，树的端点只有0/1构成，每个节点用下标来表示所需要的参数个数，比如\(1_2\)表示这个节点为\(1\)，其需要两个参数节点。

树的异或

定义\(L(Ω)\)表示\(Ω\)中所有子节点的深度都达到\(l\)的全子树集合。
定义⊕表示两个0/1树的异或：其返回一个子树，该子树与这两个树截断的形状相同，并且对应的每一个节点上的值都是这两个树对应节点异或的结果：
\[a⊕_{treewise}b=π_k(a)⊕_{bitwise}k\] 在这里，截断\(π_k(a)\)是指，将树\(a∈L(Ω)\)按照\(k\)的样子进行修剪，但是不改变\(a\)中节点的内容:

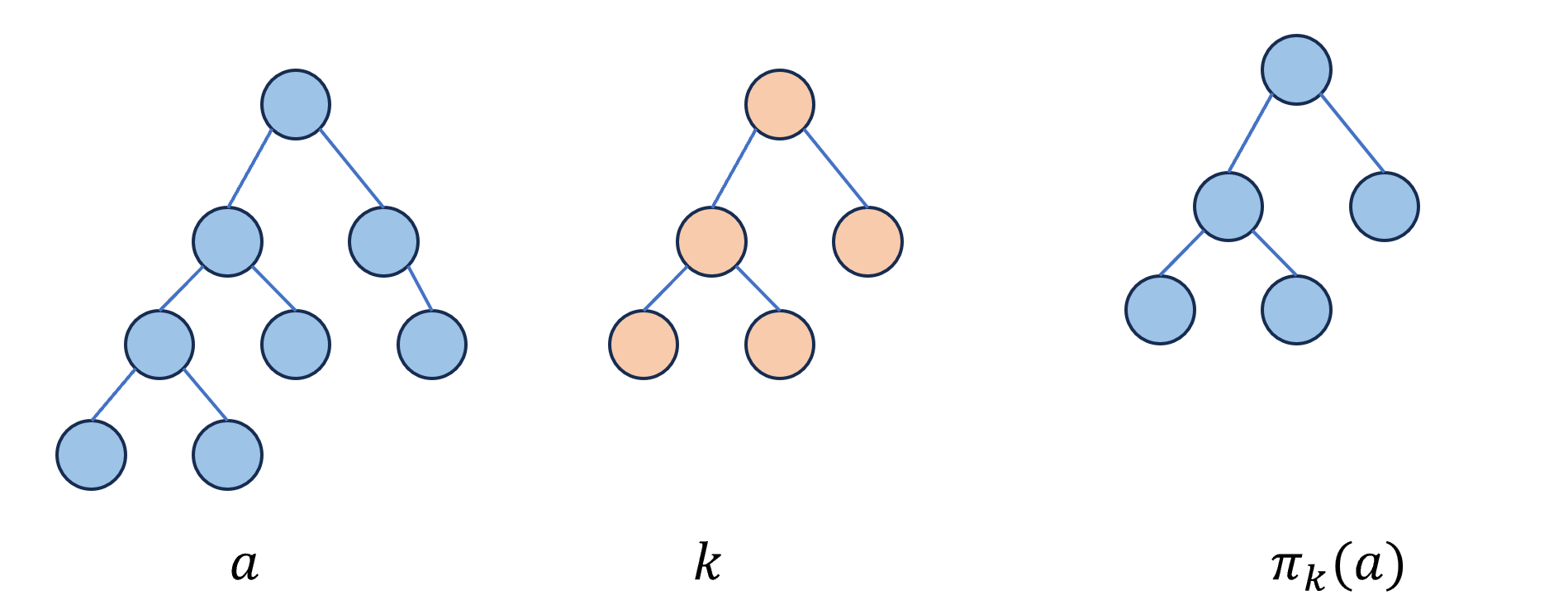
定义一个\(r×r\)的置换矩阵(permutation matrix)\(σ_a\)，表示有多少种不同的情况可以使得\(i⊕j=π_j(a)\)：
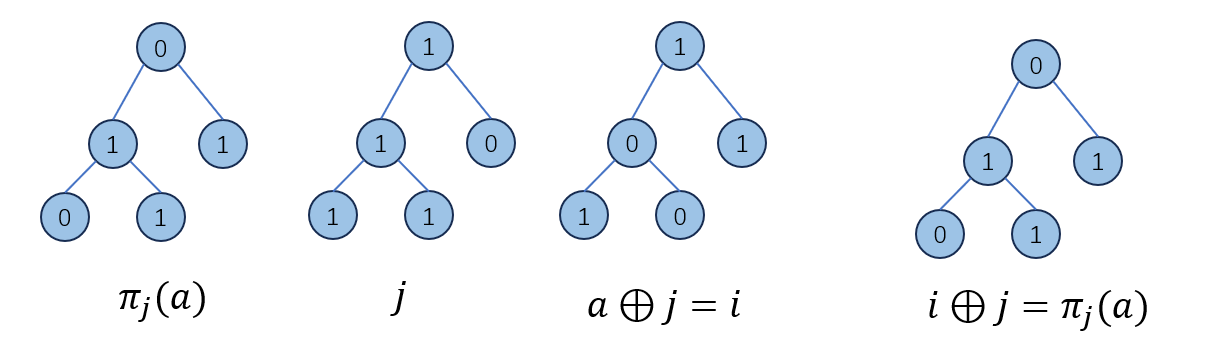
\[(σ_a)_{i,j}=δ((a⊕i)=j)\]

下图展示了\((σ_a)_{i,j}\)的意义：

理论3：

如果\(m,n,y∈Ω\)，\(a∈L(Ω)\)，有：
\[rec_{m,n}(y)=rec_{a⊕m,a⊕n}(a⊕y)\]

在证明之前，需要明确几条树的异或的性质：

1. 如果\(a⊕m=a⊕y\)，那么\(m=y\)，反之亦然。
   
2. 对于异或运算中较小的那棵树，异或只改变树的标签，不改变形状。因此异或运算前后两个树的common region 应该是相同的：
   \[C(m,n)=C(a⊕m,a⊕n)\]
3. 同理，异或只改变树的标签，不改变形状，有： \[(a⊕m)∈Γ(a⊕y,l)⇔m∈Γ(y,l)\]

根据上面三条性质，有： \[\begin{aligned} rec_{a⊕m,a⊕n}(a⊕y)&=∑_lp_l^{C(a⊕m,a⊕n)}δ(a⊕m∈Γ(a⊕y,l))δ(a⊕n∈Γ(a⊕y,\overline{l}))\\ &=∑_lp_l^{C(m,n)}δ(m∈Γ(y,l))δ(n∈Γ(y,\overline{l}))\\ &=rec_{m,n}(y) \end{aligned}\]

混淆矩阵的简化计算

现在将式子\((3-3)\)拓展到矩阵的层面。
建立一个混淆矩阵\(ℳ_y\)，其每一个元素表示\(m\)和\(n\)交叉后产生\(y\)的概率：
\[(ℳ_y)_{m,n}=rec_{m,n}(y) \tag{3-5}\] 由种群\(x\)中的个体产生的下一代中每一个个体的存在频率用混淆向量表示为：
\[ℳ(x)=[x^Tℳ_0x,x^Tℳ_1x,x^Tℳ_2x,...,x^Tℳ_{r-1}x]\]

现在探讨混淆矩阵和混淆向量之间的关系，假定现在有一个树\(0\)为将shape \(G\)中的全部“=”置换为“0”得到的子树，表示为\(0^G\).\(𝒶∈L(G)\)表示将个体\(y∈G\)用\(0\)扩增到深度为\(l\)的全树，且每个节点的子节点数目都添加到\(i_m\)所构成的子树：

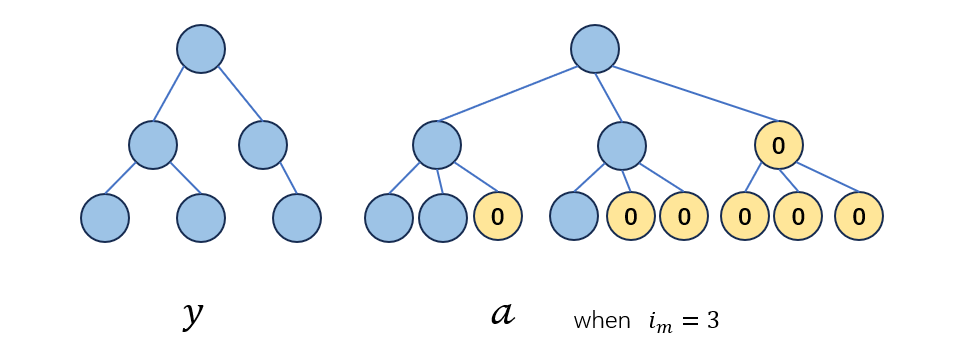
那么，\(y,a,0^G\)存在如下的关系：
\[(ℳ_y)_{m,n}=rec_{m,n}(y⊕0^G)=rec_{m,n}(a⊕0^G) \tag{3-6}\] 现在，想要找到一个树\(a^{-1}\)，根据理论3，使得如下的式子成立，以消除括号中的式子：
\[rec_{a^{-1}⊕m,a^{-1}⊕n}(a⊕0^G⊕a^{-1})=rec_{a^{-1}⊕m,a^{-1}⊕n}(0^G) \tag{3-7}\] 那么有\(0^G=a⊕0^G⊕a^{-1}\)，求得\(a^{-1}=a\)，那么式\((3-6)\)可以改写为：
\[\begin{aligned} (ℳ_y)_{m,n}&=rec_{m,n}(y⊕0^G)\\ &=rec_{a^{-1}⊕m,a^{-1}⊕n}(0^G) \\ &=rec_{a⊕m,a⊕n}(0^G) \end{aligned}\tag{3-8}\] \(a\)与\(m\)的异或为\(0\)表示\(m\)与\(y\)有一部分是相同的。
根据\((3-5)\)，\((3-7)\)可以改写成：
\[rec_{a⊕m,a⊕n}(0^G)=ℳ_{a⊕m,a⊕n}(0^G) \tag{3-9}\] 现在令\(a⊕m=w\),\(a⊕n=v\)，那么\(a⊕w=m\)，\(a⊕v=n\)，有：
\[δ(a⊕w=m)=(σ_a)_{w,m}\] \[δ(a⊕v=n)=(σ_a)_{v,n}\] 代入\((3-9)\)：
\[\begin{aligned} M_{a⊕m,a⊕n}(0^G)&=∑_v∑_w(σ_a)_{w,m}ℳ_{w,v}(0^G)(σ_a)_{v,n}\\ &=∑_v(σ_aℳ(0^G))^T_{m,v}(σ_a)_{v,n}\\ &=(σ^T_aℳ(0^G)σ_a)_{m,n} \end{aligned}\tag{3-10}\]

下图给出了一个\(G,y,a,m,n,w,v\)的例子：

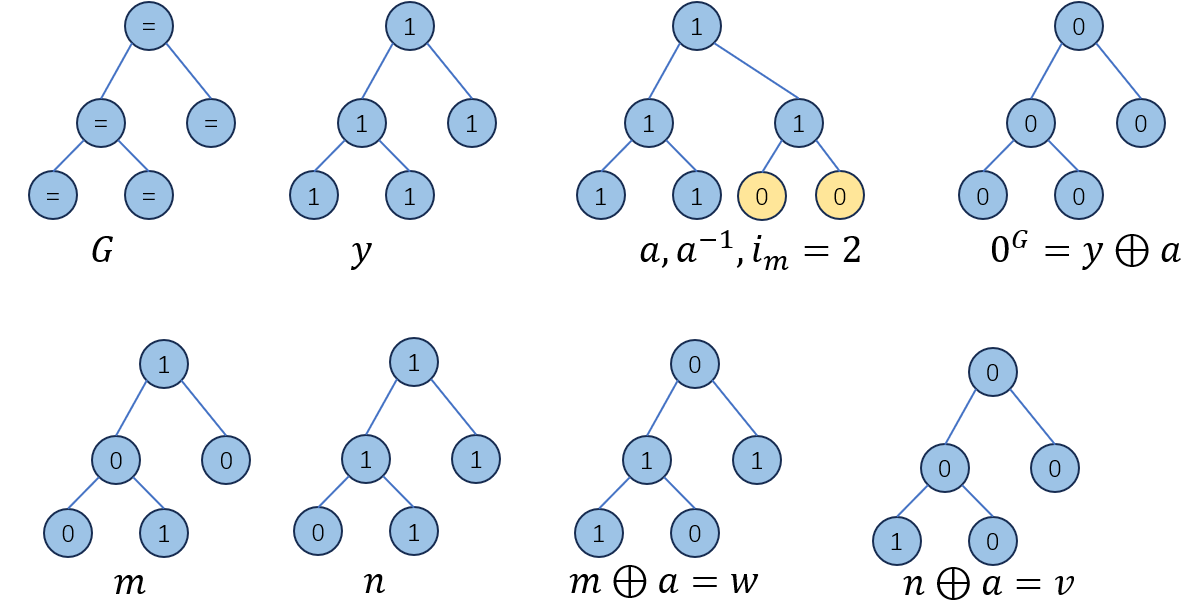
根据式子\((3-6)\)到\((3-10)\)，对于shape \(G\)而言，存在\(0^G\)的混淆矩阵\(M_{0^G}\)使得如果\(y∈Ω\)在shape \(G\)中，有：
\[ℳ_y=σ_a^Tℳσ_a\] 进一步的：
\[(ℳ_y)_{m,n}=(σ_a^Tℳ_{0^G}σ_a)_{m,n} \tag{3-11}\] 通过式子\((3-11)\)，两个亲本个体\(m,n\)交叉产生的任何个体的概率最终都可以被简化为两部分：

• \(m,n\)在某处交叉是否有可能在生成\(y\)
  
• \(m,n\)交叉生成\(0^G\)的概率

利用混淆矩阵计算的0/1树的例子

下面给出了论文中一个如何使用\(ℳ_{0^G}\)和\(σ_a\)求解\(ℳ_y\)的例子。
假设现在\(l=2\)，且每个节点只有一个参数，那么\(L(Ω)=\{0,1,00,01,10,11\}\)，如果进行单点交叉，有：
\[ℳ_{0^{==}}=ℳ_{0^{00}}=\left[\begin{array}{c|ccccccc} &0&1&00&01&10&11 \\ \hline0&0&0&1&0&0&0\\ 1&0&0&1&0&0&0\\ 00&0&0&1&0&1/2&0\\ 01&0&0&1&0&1/2&0\\ 10&0&0&1/2&0&0&0\\ 11&0&0&1/2&0&0&0\\ \end{array}\right]\] \[σ_{10}^T=\left[\begin{array}{c|ccccccc} &0&1&00&01&10&11 \\ \hline0&0&1&0&0&0&0\\ 1&1&0&0&0&0&0\\ 00&0&0&0&0&1&0\\ 01&0&0&0&0&0&1\\ 10&0&0&1&0&0&0\\ 11&0&0&0&1&0&0\\ \end{array}\right]\]

如果要计算\(ℳ_{10}\)，有：
\[ℳ_{10}=σ_{10}^Tℳ_{0^{00}}σ_{10}=\left[\begin{array}{c|ccccccc} &0&1&00&01&10&11 \\ \hline0&0&0&0&0&1&0\\ 1&0&0&0&0&1&0\\ 00&0&0&0&0&1/2&0\\ 01&0&0&0&0&1/2&0\\ 10&0&0&1/2&0&1&0\\ 11&0&0&1/2&0&1&0\\ \end{array}\right]\]