交叉算子的建模和比较

Poli, Riccardo & Langdon, W.. (2001). On the Search Properties of Different Crossover Operators in Genetic Programming.

背景

回顾遗传算法的schema theory:
\[P(H,t+1) \geq P(H,t) \frac{f(H,t)}{\overline{f}} [1-p_c \frac{\Delta(H)}{L-1}(1-P(H,t)\frac{f(H,t)}{\overline{f}})] (1-p_m)^{o(H)}\] 对遗传算法建立的schema theory中Don't care在不同的位置上对于个体的印象体现在定义距上\(Δ(H)\)。通过上式可以发现，定义距的改变对整个式子的影响是线性关系。(相当于\((a-ax)c=a-bx\),\(x\)发生变化的影响是线性的)
然而在遗传编程中，Don't care在不同的层级上对搜索的影响并不是线性的，因此交叉造成的破坏效应(disruption)也是不同的。

这篇论文中作者对三种不同的交叉算子: 标准交叉、单点交叉、均匀交叉在进化过程中所做的信息交叉的作用进行了数学建模，然后进行了分析对比。

结果是否可靠？

衡量动态性的指标

在这篇文章中，作者亲本中的一个在交叉过程中移走的节点个数代表亲本之间的交换的遗传信息的信息量\(E[S]\)。为了更好的定义和描述交叉过程中亲本之间遗传信息的交换过程，作者还定义了如下的指标。

• 节点密度函数(node density function)
  是树\(h\)在深度\(d\)下的节点数量与整个树的节点数量的比值。如果在交叉过程中每个节点被选中成为交叉点的概率是相同的，那么其同等于在选择树\(h\)的前提下，选择深度为\(d\)的节点作为交叉点的条件概率，记为\(p(d|h)\)。

那么，如果记\(S(d,h)\)表示的是树\(h\)在深度\(d\)以下的期望的单个子树大小（“期望”表示树是full树且\(d\)的每个节点都有大小相同的子树），那么\(p(d|h)S(0,h)\)表示树\(h\)上深度为\(d\)的结点个数。其中\(S(0,h)\)表示树\(h\)所有节点的个数。
\(p(d|h)\)和\(S(d,h)\)之间有如下的关系：
\[\begin{aligned} S(d,h)&=\frac{\text{nodes at depth }≥ d}{\text{nodes at depth }d}\\ &=\frac{\sum_{x=d}p(x|h)S(0,h)}{p(d|h)S(0,h)}\\ &=\frac{\sum_{x=d}p(x|h)}{p(d|h)} \end{aligned}\]

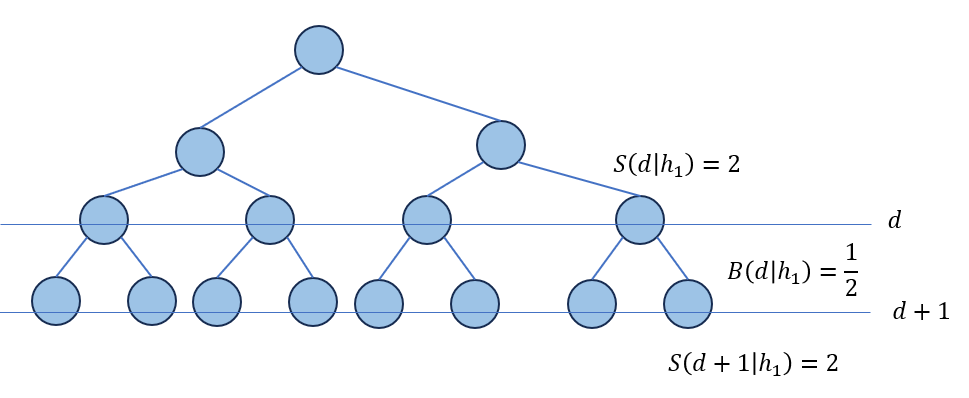
那么深度为\(d\)的节点的平均连接数可以定义为：
\[\frac{1}{B(d|h)}=\frac{\text{nodes at depth }d}{\text{nodes at depth }d+1}=\frac{S(d,h)p(d|h)}{S(d+1,h)p(d+1|h)}\] \[B(d|h)=\frac{S(d+1,h)p(d+1|h)}{S(d,h)p(d|h)}\]

交叉算子

标准交叉

原始的遗传编程中所定义的交叉算子称为标准交叉(standard crossover)，其操作是随机选取两 个树上任何一个节点，然后节点下方的子树发生交换。

单点交叉

单点交叉(one-point crossover)是作者在之前的论文中定义的一种交叉方式，其操作是随机选取两个亲本拓扑结构相同的区域(又称common region，发生在common region中的交叉不会改变种群中schema的拓扑结构)中的节点，然后节点下方的子树发生交换。

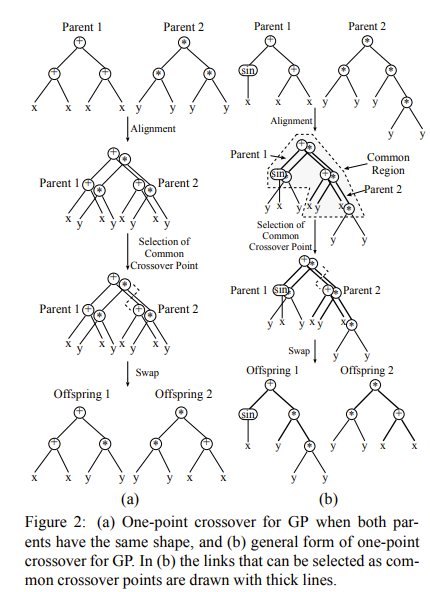
均匀交叉

均匀交叉(uniform distribution)是作者在这篇论文中提出的一种新的交叉算子。其操作是：对于common region中的节点，他们都有\(p_s\)的概率发生点对点的交换。如果这个交换发生在common regions最下层的节点(称为边界节点)，那么节点下方的子树也一同进行交换。

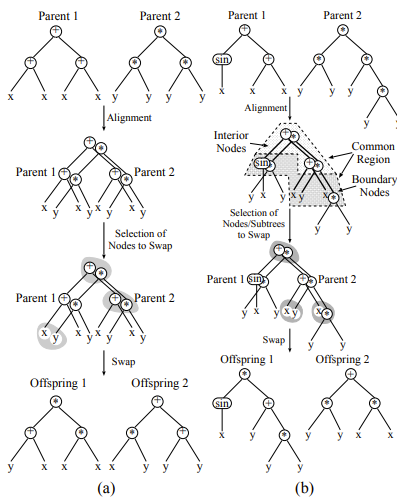
对交叉算子的动态性建模

如果设计交叉发生树\(h_1\)的深度\(d_1\)和树\(h_2\)的深度\(d_2\)下，那么整个种群中所有被交换的节点的数量可以用如下的式子表示：
\[E[S_r]=∑_{d_1,d_2}∑_{h_1,h_2}p(h_1)p(h_2)p(d_1,d_2|h_1,h_2)S(d_1,h_1)\tag{2}\] 式(2)的前半部分表示的是选择\(h_1,h_2\)后选择\(d_1,d_2\)的全概率。\(S(d_1,h_1)\)表示的是\(h_1\)的深度\(d_1\)上的一个子树被交换给了\(h_2\)的节点数量，这也是\(h_2\)得到的节点的数量。

标准交叉

对于标准交叉，种群中两个亲本的交叉点的选择是完全独立的，因此有：
\[p(d_1,d_2|h_1,h_2)=p(d_1|h_1)p(d_2|h_2)\tag{3}\]

那么信息交换的部分可以表示为:
\[\begin{aligned} E[S_{std}]&=∑_{d_1,d_2}∑_{h_1,h_2}p(h_1)p(h_2)p(d_1|h_1)p(d_2|h_2)S(d_1,h_1)\\ &=∑_{h_1}∑_{d_1}p(h_1)p(d_1|h_1)∑_{h_2}p(h_2)∑_{d_2}p(d_2|h_2)S(d_1,h_1)\\ \end{aligned} \tag{4}\] 由于\(∑_{h_2}p(h_2)∑_{d_2}p(d_2|h_2)=1\)，即选择种群中另一个个体的某个深度下的节点作为交叉节点的概率，所有的概率之和应当为1，那么有：
\[ E[S_{std}]=∑_{h_1}p(h_1)∑_{d_1}p(d_1|h_1)S(d_1,h_1) \tag{5}\]

单点交叉

对单点交叉而言，两个亲本的交叉点选择到的深度应当是相同的，也就是说当\(d_1≠d_2\)时，\(p(d_1,d_2|h_1,h_2)=0\)，那么有：
\[∑_{d_2}p(d_1,d_2|h_1,h_2)=∑_{d_1}p(d_1,d_1|h_1,h_2)=∑_{d_1}p(d_1|h_1,h_2) \tag{6}\]

\[\begin{aligned} E[S_{1pt}]&=∑_{d_1,d_2}∑_{h_1,h_2}p(h_1)p(h_2)p(d_1,d_2|h_1,h_2)S(d_1,h_1)\\ &=∑_{h_1}p(h_1)∑_{d_1}S(d_1,h_1)∑_{h_2}p(h_2)p(d_1|h_1,h_2) \end{aligned} \tag{7}\]

式\((7)\)当中的\(∑_{h_2}p(h_2)p(d_1|h_1,h_2)\)可以看做是对\(h_1\)而言，在其他任意一个树上选择交叉点在\(d_1\)上后，\(h_1\)的\(d_1\)上选择交叉点的概率。模仿贝叶斯公式，可以将上述式子定义为：
\[p_{1pt}(d_1|h_1)=∑_{h_2}p(h_2)p(d_1|h_1,h_2)=p(d_1 | \text{other trees in gen }t)p(d_1|h_1)=p_{1pt}(d_1|h_1,t) \tag{8}\] 根据式子(8)的理解，\(p_{1pt}\)中“选择另一个树中\(d_1\)上的节点”的概率与进化代数\(t\)应当是有关的。

均匀交叉

均匀交叉是一种点对点的交叉，因此交换的节点数量应该为可以交换的节点数量与每个节点交换的概率的乘积。可以交换的节点的数量需要分两种情况讨论：第一种情况是发生交换的节点在common region的内部；第二种情况是发生交换的节点在common region的边界上，此时需要将这个节点以下的子树也进行交换。如果设\(N_i(d_1|h_1,h_2)\)表示深度为\(d_1\)上的，非边界的节点，\(N_b(d_1|h_1,h_2)\)表示深度为\(d_1\)的边界节点。那么有：
\[E[S_{uni}]=p_s ∑_{h_1,h_2}p(h_1)p(h_2)∑_{d_1}[N_i(d_1|h_1,h_2)+N_b(d_1|h_1,h_2)S(d_1,h_1)] \tag{9}\] \(h_1\)的\(d_1\)层的所有的节点数量应当是上一层(如果交叉还可以发生在\(d_1\)，那证明上一层是没有边界节点的)的所有的节点数量与每个节点拥有的连接的数量的乘积：
\[\text{\# nodes in } d=B(d_1-1|h_1)N_i(d_1-1|h_1,h_2)\tag{10}\] 那么有：
\[N_b(d_1|h_1,h_2)=B(d_1-1|h_1)N_i(d_1-1|h_1,h_2)-N_i(d_1|h_1,h_2) \tag{11}\]

将(11)带入(9)，得到：
\[\begin{aligned} E[S_{uni}]=&p_s ∑_{h_1,h_2}p(h_1)p(h_2)∑_{d_1}[N_i(d_1|h_1,h_2)+N_b(d_1|h_1,h_2)S(d_1,h_1)]\\ =&p_s ∑_{h_1,h_2}p(h_1)p(h_2)∑_{d_1}[N_i(d_1|h_1,h_2)\\ &+[B(d_1-1|h_1)N_i(d_1-1|h_1,h_2)-N_i(d_1|h_1,h_2)]S(d_1,h_1)]\\ =&p_s∑_{h_1,h_2}p(h_1)p(h_2)[S(0,h_1)\\ &+∑_{d_1=1}N_i(d_1|h_1,h_2)(1-S(d_1,h_1))+B(d_1-1|h_1)N_i(d_1-1|h_1,h_2)S(d_1,h_1)]\\ =&p_s∑_{h_1,h_2}p(h_1)p(h_2)[S(0,h_1)+∑_{d_1=1}N_i(d_1|h_1,h_2)(1-S(d_1,h_1)+B(d_1|h_1)S(d_1+1,h_1)] \end{aligned} \tag{12} \]

并且，当树是full，且所有的子树大小都相同的前提下存在如下关系：
\[S(d_1,h_1)=1+B(d_1|h_1)S(d_1+1,h_1)\] 那么(12)可以简化为：
\[E[S_{uni}]=p_s ∑_{h_1,h_2}p(h_1)p(h_2)S(0,h_1)=p_sE(S(h_1)) \tag{13}\] 其中\(E(S(h_1))\)表示\(h_1\)在full，每一层级子树大小相同下的节点的数量。

交叉算子的分析和比较

标准交叉和单点交叉

来看进化过程中标准交叉和单点交叉的公式：
\[ E[S_{std}]=∑_{h_1}p(h_1)∑_{d_1}p(d_1|h_1)S(d_1,h_1) \tag{5}\] \[\begin{aligned} E[S_{1pt}]&=∑_{h_1}p(h_1)∑_{d_1}S(d_1,h_1)∑_{h_2}p(h_2)p(d_1|h_1,h_2) \\ &=∑_{h_1}p(h_1)∑_{d_1}S(d_1,h_1)p_{1pt}(d_1|h_1,t) \end{aligned} \tag{7}\]

两者的差异在于\(p(d_1|h_1)\)和\(p_{1pt}(d_1|h_1,t)\)：前者不会随着进化的代数发生变化，后者因为和种群有关因此会随着进化的代数发生变化。
在进化的初期，如果种群中的diversity比较大，也就是说common region的区域比较小的话。对于较大的\(d_1\)来说，有\(p(d_1|h_1)>>p_{1pt}(d_1|h_1,t)\)，也就是说，此时标准交叉更倾向于对树更靠近低端的部分进行交叉，这种操作对拓宽搜索并没有帮助；对较小的\(d_1\)来说，\(p_{1pt}(d_1|h_1,t)>>p(d_1|h_1)\)，也就是说，在进化的初期单点交叉比标准交叉更容易发生在靠近树顶的位置，更有助于在进化初期拓宽搜索。

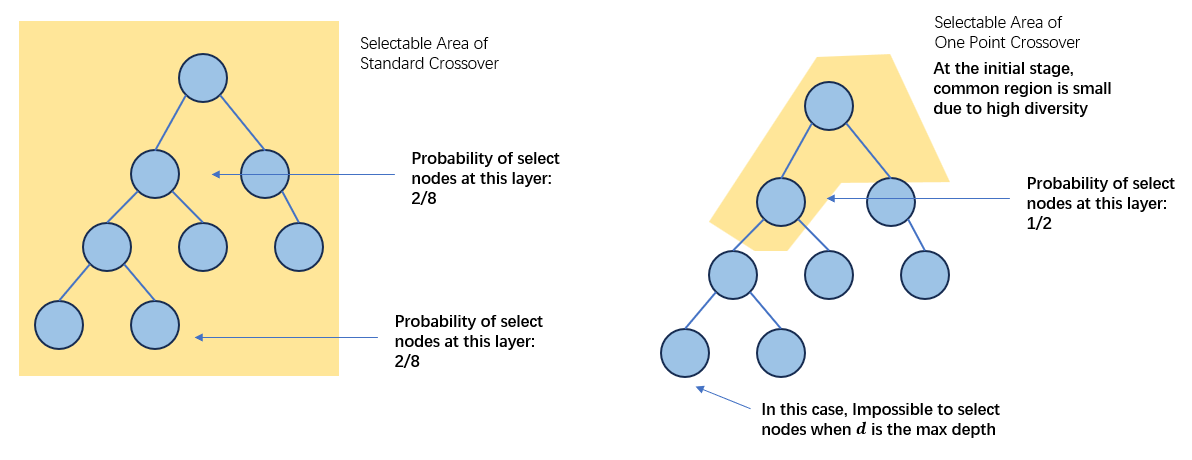
从上面的分析可以看出，单点交叉是通过common regions限制可以进行交叉的节点从而在进化的初期增大上层节点被选择的概率。
现在来讨论进化初期节点交换的充分程度，作者假设了最大的信息交换发生在树的顶端（这个假设是错误的），此时除了根节点之外的所有的节点都交换到了另一个亲本，有\(E(S)\)最大。虽然两种交叉都有可能发生类似的情况，但是由于单点交叉限制在了common region内，单点交叉进行这种最大情况的可能性要远远高于标准交叉，也就是说，单点交叉的全局性要优于标准交叉。

在进化的后期，由于种群多样性的减小，种群中个体的拓扑结构逐渐趋同，那么common region的面积会增大，当种群中所有个体的拓扑结构都相同时，单点交叉和标准交叉完全相同：
\[\lim_{t→∞}p_{1pt}(d_1|h,t)=p(d_1|h_1)\] 也就是说，随着进化的进行，单点交叉的全局性会逐渐减小，最终趋同于标准交叉。

均匀交叉和标准交叉/单点交叉

均匀交叉的本质是对一个树的common regions中的节点进行概率扫描。在进化初期，如果多样性足够的话（也就是从根节点开始的common region面积非常小的话），均匀交叉几乎没有可能会交换靠近低层的节点，从而增加搜索的全局性。
随着时间的推移，common regions的面积会逐渐增大，此时理论上边界节点在common regions中的占比会越来越小，因此会有越来越多的节点（*注：？不一定，参考下图）和越来越小的树（*注：也是不一定的，只有在树是full且每一层的所有子树大小相同的前提下这个推论才是一定正确的）被交换，直到运行结束时，每棵树上的所有节点都可以被自由选择进行交换。

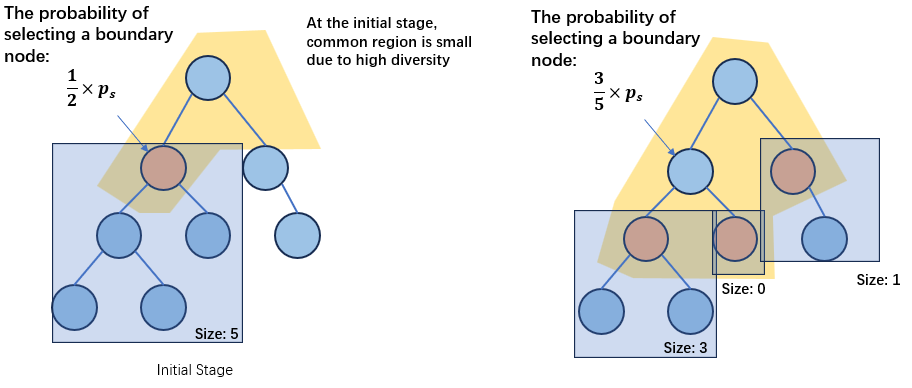
与单点交叉不同的是，均匀交叉的全局性依赖于对\(p_s\)的选择，\(p_s\)一旦被选择，均匀交叉的全局性/局部性将不会随着进化过程发生改变。
\(p_s=0.5\)是理论上两个亲本的信息交流达到最大值的设定，但是随着进化过程中两个亲本完全相同的结点越来越多，“无效”的交换也会越来越多，如此均匀交叉也会趋于收敛。

结论

在进化的初期，标准交叉相比于其他两个交叉算子更容易将交叉发生在根节点上，标准交叉带来的全局效应非常弱。因此，标准交叉非常依赖于初始种群在搜索空间中的采样范围，如果初始种群的多样性本来就不高，标准交叉比其他两种交叉更难跳出这个采样范围。在进化后期的单点交叉也有这种表现。
事实上，单点交叉和标准交叉都是将树的某个部分整体进行交换，实际上在搜索空间中的行为是对亲本进行插值采样。因此，这两种交叉都依赖于初始种群对搜索空间的采样范围。
上述的分析表明，在使用单点交叉和标准交叉时，初始种群的大小设置的尽可能大，并且应该在拓扑结构和语义上具有足够的多样性。
相比之下，均匀交叉更具有无偏性，因为这是一种点对点的交叉。