GP Memo

基础定义

语构和语义

语构（Syntax）

指一个个体树的拓扑结构，具体包括树整体的形状大小，每个节点上的值和连接。Standard GP中的交叉和突变是一种完全忽略个体语义的语构操作。

语义（Semantic）

指个体作为模型看待时的行为表现，这个表现通常是和数据集相关的：比如均方差/信息熵/几何信息/布尔值等等。Fitness Function也 是一种语义，但是Fitness Function对于结构过于敏感导致无法正确识别出building blocks。^{[1] [2] [3]} GP中的选择是一种忽略语构（在bloating问题出现后有时也会考虑树的大小）的操作。

子空间的划分

Schema

Schema是一种搜索空间中子空间的划分方式。可以依据各种各样的分类标准将个体归纳为子空间。对于Schema的归纳方式可以分为按照语义和按照语构进行划分。目前大部分对于schema的定义都是基于语构的，也就是拓扑结构相似的一组子树。这也是最早的对GP中schema的定义。这样定义的原因是，交叉和突变都完全基于语构进行，采用语义的schema无法清楚的描述交叉产生的后代和亲本之间的关系 ^[4]。^[1] 中采用了一种强制限定语义值的方式才能勉强实现在保证亲本和后代关系的前提下对语义进行归纳。

Building Blocks

不管对于Building Blocks具体的定义为何，GP中对Building Blocks存在两点共识：

• Building Blocks是比Schema粒度更细的进化单元，它既是Schema又是其他的高阶Schema的一部分。
  
• Building Blocks上携带了Schema/个体的遗传信息。这些遗传信息有利于子种群进化。

^[4] 中对GP的Building Blocks的认知基本上照搬GA：“building blocks是低阶、受扰乱程度低、并且可以存活数代的schema”。Poli则认为Building Blocks是交叉过程中两个亲本必须各自持有、才能在后代中产生某个更高阶的Schema^[5]。^[2]中认为Building Blocks是对应语义值出现频率高的子树。前两者都是基于语构定义的building blocks，最后一个则是基于语义的Building blocks.

大部分关于Building blocks的定义都认为Building blocks应当携带两类信息：Building blocks内部的拓扑结构和其在个体中的位置。

• Building Blocks的拓扑结构由内部有意义的部分确定，这部分的拓扑不允许修改，这部分确定了Building blocks自身的语义；
  

• Building blocks在个体当中的哪个位置则由通配符来提供。Building blocks当中的通配符部分描述了Building blocks和树当中的其他部分的相对位置关系。这其中关于Building blocks的定义又分为两种：building blocks的根节点为通配符和非通配符的定义。

  • 当building blocks的根节点是通配符时，building blocks在个体中的位置并没有被固定下来，它可以连接一个树的任何一个部分 ^[4]。事实上，^[4]认为的building blocks完全和相对位置无关，其对building blocks的定义是语法树和其需要出现一个个体当中必须的出现次数。
    这种定义的根据是认为GP的搜索动力学特性与GA的搜索动力学特性相似：第一阶段找到Building blocks，第二阶段通过Crossover将building blocks整合到高阶的schema中，第三阶段将高阶的Schema扩散到整个种群中 ^[6] 。在这个过程中，在前两个阶段crossover的作用都只是把building blocks凑齐，这个过程并没有考虑位置关系。
    这样定义的问题是，由于搜索中语义和语构的非统一，Fitness Function对个体的语构非常敏感，因此凑齐了building blocks的高阶Schema中的个体未必具有高fitness可以让这个schema扩散到种群当中。（很有可能在很短的数代之内就已经消散了）。
    
  • 当building blocks的根节点不是通配符时，代表着building blocks描绘了一整个个体和building blocks之间的相对位置关系，比如^[5]中提出的Hyper schema和^[7]当中的结点schema。

对Building blocks定义的可解释程度决定了对Building blocks的提取方式：

• 当building blocks的定义缺乏可解释性的时候（比如，认为building blocks是携带“遗传信息”的元实体），目前可以做的方法是 (1) 遍历整个个体，选取满足关心的特点（一般来说是出现频率和深度等）的子树作为building blocks ^{[2] [8] [9]}。如果使用building blocks的目的是为了加速搜索，这种方法需要考虑遍历所花费的计算量和找到building blocks之后其引导搜索导致的计算量的减少之间的花费是否值得。（2）将亲本反复多次交叉，剩下的部分为building blocks ^[4]。
  这种提取方式往往会选择“出现频率高”是满足一个子树是building blocks的必要条件。频率是一种building blocks贡献程度的间接体现方式，根据building block hypothesis（后面会详述）的推论，贡献高的building blocks会因为其提升了个体的fitness而更容易被选择繁殖，从而在整个种群中扩散。

• 当building blocks是一种较为容易理解的定义时（building blocks是schema或者是目标解的一部分），building blocks可以直接从schema或者是目标解上进行划分 ^{[5] [10]}。

GP的搜索动力学

选择和交叉的作用

在^[4]中，GP的building blocks hypothesis基本上照搬GA的building blocks hypothesis ^[11]：在过去的搜索中找到的低阶的、具有高fitness的building blocks组成的个体在随后的数代当中具有高的fitness ^[4]。
因此，Building Block Hypothesis认为：GP的搜索动力来自于通过选择和交叉的联合作用（语义和语构空间的联合作用）可以发现building blocks并且将它们组合到一起。
^[12]通过实验说明：交叉将会传递亲本中优秀部分到子代中，使得大部分子代可以继承至少来自一个亲本的优秀部分。

在后续的文献中，一部分人认为Crossover并不能起到非常好的促进进化的作用 ^[13]，GP真正的搜索原动力来自于选择起到的在搜索空间中有偏向性的采样。
^[7] 通过实验进一步的说明了GP搜索的行为：种群中的个体以递归方式从根节点自上而下收敛，每一级节点逐渐"冻结"为函数集中的一个给定函数 。
GP从上到下开始收敛的猜测是，越靠近根节点的结点对个体进化的影响越大（也就是所谓的携带的遗传信息量更高），因此更容易影响进化过程，从而主导进化。从这个角度来看，GP中对有限个采样点分配的竞争可能发生在同一个深度/位置的不同节点之间。
因此，进化总是会从影响最大的部分开始，随着影响部分最大的部分在种群中逐渐被固定下来，此时其不再主导进化，次影响最大的部分开始主导进化。如果对进化的影响和个体结点所处的深度成正比，那么进化过程就会是从上到下开始固定节点。

Schema Theory / Markov 模型 / Price Equation

不管是哪种对schema的定义方式，schema在种群当中的传播理应遵循Schema Theory。它描述了一个特定的schema在下一代当中的采样率是如何变化的。

最早的Schema Theory是从扰乱，也就是属于Schema的个体如何通过变异被破坏而导致不再属于Schema的视角进行的描述的^[4]：
\[p(H,t+1)= (1-p_c)p(H,t)+p_c\underline{p(H,t)(1-[P_d(h,H)]_{cap})}\] \[P_d(h,H)=\frac{D_{fixed}(H)+D_{var}(h,H)}{Size(h)}\] 扰乱的视角存在许多问题（在^[4]中作者自己列举出了7条问题）， 根本原因是语义和语构空间的不均匀映射导致distruptive rate实在是太大了，以至于对schema的行为无法精准的预测。
在GA中，对GA的搜索景观的要求是信息密度在搜索空间中的分布是均匀的，这个表现为GA的schema theory中，含有定义距\(-ΔH\)的一项与schema的disruption rate成正比关系:
\[P_d(H)\propto -ΔH\] 但是在^[4]的定义中，这样的正比关系对个体虽然存在，但是由于树形结构和\(D_{var}(h,H)\)的加入导致无法判断\(D_{var}(h,H)\)在每个个体中的变化关系，从而无法判断对于整个schema的子种群，\(P_d\)与\(ΔH\)还是否成正比关系，因此schema theory的作用被减弱。

其后Poli提出的Schema Theory则是从构建，也就是两个亲本交叉如何保留让个体属于Schema的角度进行描述的^[5]： \[p(H,t+1)= (1-p_c)p(H,t)+p_c\underline{α_c(H,t)}\] \[α_c(H,t)=∑_{k,l}\frac{1}{|C(G_k,G_l)|}×∑_{i∈C(G_k,G_l)}p(U(H,i)∩G_k,t)p(L(H,i)∩G_l,t)\] 在构建的叙述中，只有交叉发生在两个亲本的Common Regions当中时，Schema的拓扑结构才可能被保留。在Common Regions当中进行的交叉的另一个作用是可以在进化的初期增大根节点被选择作为交叉的概率，以扩大搜索的范围（增加种群多样性）^[14]。

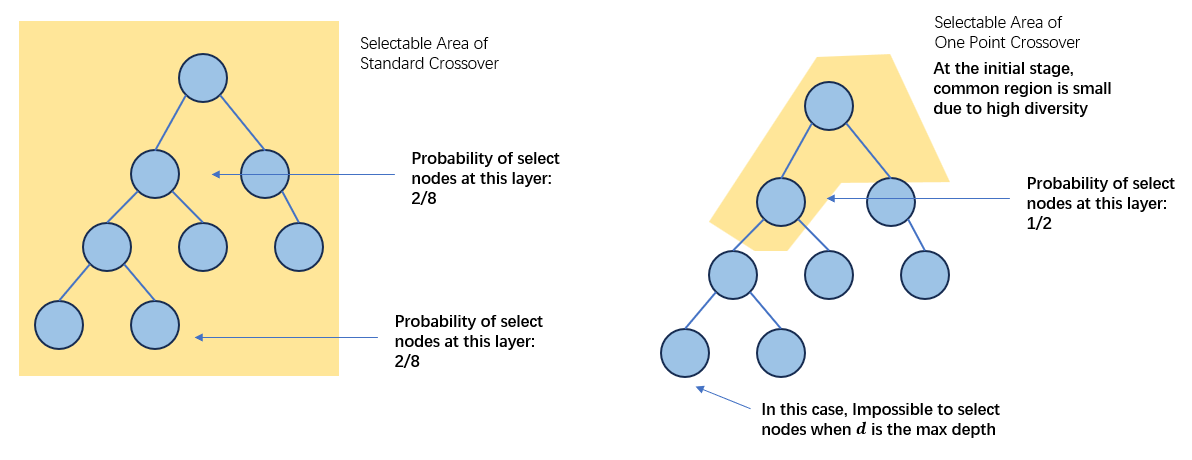
构建角度叙述的问题在于，构建角度的Schema Thoery无法描述具有什么样子的Schema才能在进化过程中胜出。具体的原因是，构建只描述了构建目标来源所需要具备的特征（各自持有构建目标的一半），缺少了对构建目标本身特征的描述（比如定义距、阶等等）。

Schema Theory中的一个问题是，Schema theory将fitness function视为黑箱看待，并没有清楚的描述fitness function和schema之间的作用关系。 ^[32]

马尔科夫链模型通过建立一步概率转移矩阵来描述种群中的个体的转移变化，^[5]认为马尔科夫模型和schema theory其实是对同一行为的不同角度下的描述。
马尔科夫链最大的问题是，一步概率转移矩阵在建立时要求状态必须是完备的（必须考虑所有的状态转移情况），也就是说，GP的一步概率转移矩阵需要针对整个搜索空间才可以完整描绘出GP的动态性。马尔科夫链模型存在“维数灾”问题，所以在进化计算的领域中对马尔科夫链模型的研究转向了对一步概率矩阵的特征分析（比如特征值到底对应了算法的哪些表现）^[32]。

另一些文献中使用了Price Equation ^[15]对Schema的采样率变化进行建模。 利用Price公式的对GP中schema的采样率变化描述如下^[7]：
\[\Delta |h|=Cov(p_s(r_i),member(h,r_i))+E(\omega_i \Delta z_i)\] 这个公式的第一项协方差项描述了选择作用，第二项期望项则描述了遗传变异的作用。如果不考虑突变，Price Equation也是对Schema Theory的另一种描述方式：方差项对应Schema Theory的第一项\((1-p_c)p(H,t)\)，期望项对应\(p_c{α_c(H,t)}\)。

研究Price Equation的原因可能是，在Exact Schema Theory之前，Schema Theory只能给出概率的下界，然而Price Equation可以给出一个准确的值。

GP中存在的问题

GP中语构和语义的映射关系

GP中最大的问题是语构空间和语义空间的映射并不是一对一的，同一个语义值对应了若干种不同的个体，并且GP的树形结构不能保证结构的变化到语义的变化是连续且同等的^{[3] [31]}。这些特性和GA是截然不同的（GA中的二进制位串基本上可以保证语义和语构是一一对应的）。

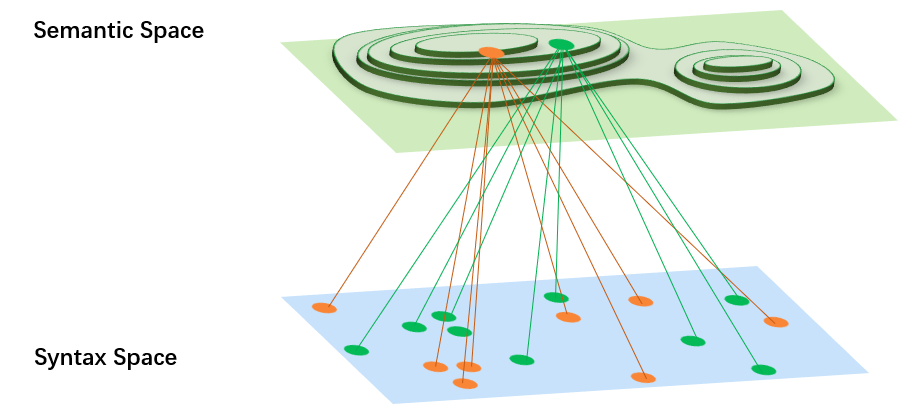
又，根据^[34]认为个体信息被压缩到fitness的过程当中损失了大量的信息，在GP中语义空间中的样本点数应当远远小于语构空间中的样本点数。

这些问题具体表现为如下几个方面：

• 同一个结构上的schema所对应的个体中的fitness呈现高方差的特性^[4]。
  
• 哪怕是对个体进行非常轻微的突变，所带来的语义上的变化也有可能非常巨大^[4]。
  
• 此外，搜索后期个体树大小的无限膨胀（又称为bloat）也与语义和语构的空间映射有关：在进化的后期，个体树会产生相互抵消的子树，这些子树对个体的语义基本上没有改变，但是会增大个体的大小。^{[16] [17]} 关于bloat的问题在之后的一节中还会继续讨论。
  
• GP中基于语构的building blocks极大的依赖于语境(contexts)，同一个building blocks可以使得某些个体表现出高fitness的性质，也可能不然^[12]。

缓解的方法

• 根据个体在语义或者语构空间中的特征进行聚类 ^[2]，即利用语构或者语义的schema，找到该schema中最能够体现某一性质的一个/一些个体来代表整个schema，从而减少语义或者是语构的数量.
  比如^{[1] [2] [3] [16]}实际上在做的事情是减少GP中语义和语构之间冗余的映射关系，从而尽可能的让GP实现语构到语义一对一的映射，以提高GP的性能。

• 将搜索限定在某些子空间内。这种方法的意义是通过减少搜索需要面对的语义-语构的映射数量来简化复杂的映射。
  限制/划分子空间的方式：

  • 针对crossover过程，比如在crossover之前判断两者是否可以交叉，亦或者是在crossover之后检查交叉的结果是否还在子空间内（比如类保护的交叉 ^[19]）
    
  • 利用先验知识直接手动进行划分（比如最开始的ADF[^36]）
  • 根据现在找到的个体在语义/语构空间当中的聚集程度，或者是在fitness landscape当中的相对位置，进行启发式的划分(*niching，在GP中是否可以实现？) [^35]

Double Edge Sword?

也有一些观点认为^[32]，没有免费午餐定律NFL的其中一个导出推论是NFL只有在封闭重排的一组评估函数下才是成立的，这里“封闭重排”的意思是，有限个搜索点（语构）对应了有限个的搜索表现（语义），当这个映射关系为单射且满射时NFL成立。也就是说，对GP这种语义语构映射非单射且不均匀的算法，NFL有可能不成立，这暗示了GP可能是存在免费午餐。不过^[33]以及许多的研究认为，GP仍然符合免费午餐定律。

Bloat

bloat是指程序大小的显著增加不能带来相应的fitness的显著提升 ^[32]。

无限膨胀的原因

^[17]认为Bloat出现的原因是选择的压力作用在非单射(none-injective)的基因型和表现型上。也就是说任何解决方案都可以用多种语义相同但是结构不同的方式表达。（也就是前面所说的语义和语构的一对多映射关系。）除此之外，^[16]和^[32]中对Bloat有关的几个理论进行了讨论，可能造成Bloat的理论如下：

• protection against crossover
  bloat的存在是为了保护有效的基因片段。注意此处和ANAS中提出的显隐性关系的不同，dominace中隐性基因是完全不会表达的，而此处的bloat是会表达只是表达的作用相互抵消。

• 精度的限制
  进化中的子种群总是会朝着search landscape中fitness高的部分前进。在进化的后期想要获得fitness的提升就必须要增加精度。GP在有限分辨率的搜索空间中会以增加个体的大小的方式“临时增加”精度。

• Removal Bias
  无意义的代码片段不会对后代产生fitness的影响，而交叉的偏向性导致总是会用平均大小的子树替换较小的子树，最终导致了fitness不变的前提下个体的大小和种群的平均个体大小相互影响，最终都不断增大。并且，如果对交叉的区域不加以限制，亦或者让GP总是更有倾向性的选择靠近顶端的结点，那么就有可能发生将大的子树交换进小的个体当中的情况。

• nature of program search spaces theory
  根据对搜索空间的研究，程序的大小高于某个阈值后，fitness的分布不再随着程序大小变化。

  这个过程的证明概述如下^[32]：
  当到达某个阈值后，非图灵完备(此时不会产生功能重复的程序)的程序功能与程序长度的比例会固定，也就是说特定长度的程序所可以实现的功能数不再随着程序长度的增长而增长。该理论的证明是：将个体树的深度视为状态转移步数，将某一层的结点与下一层结点的连结视为状态转换建立一步转移概率矩阵\(M\)，发现程序的功能数是马尔科夫过程，也就是说程序的功能数与一步转移概率成指数关系 \(P=M^lV_{init}\)，但是 \([0]<M<[1]\)，因此存在阈值。
  由于在相同的fitness下长的程序的数量比短程序的数量更多，因此GP的采样更容易采到长的程序。

• crossover bias
  交叉会将种群中的程序大小分布推向第二类或者第三类拉格朗日方程，在该分布中更小的程序的出现频率更高。但是更小的程序并不能解决问题，因此选择会倾向于选择更大的程序。因此进化更倾向于每次都选择大小高于平均值的个体。

个人的理解是：在后期的一代中，两个几乎最好的个体由于交叉点没有设置限制，在不同深度上发生了交叉，此时交叉只有扰乱的效应，生成的两个个体其中一个的大小大于亲本，另一个个体的大小小于亲本。下一代中的两个个体中，较小的个体由于相比于更大的个体缺乏精度而被选择淘汰。较大的个体更容易在种群中保留，但是其fitness比第一代个体更低，为了进一步提高fitness，进化只能再继续交叉，如此个体的大小将会越来越大。

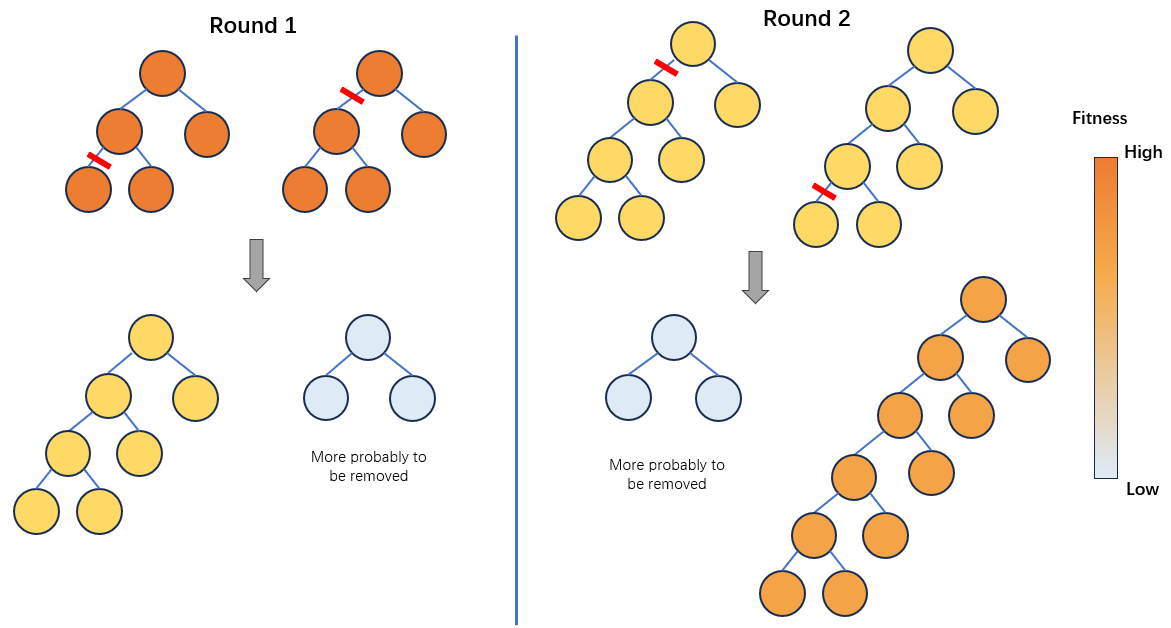
解决的方法

一些研究中将Schema theory或者price theory中的schema替换为程序的长度。这一部分研究发现了program size和选择压力是有关的，根据程序长度的schema theory：
\[E(\mu(t+1)-\mu(t))=\sum_ll\times(p(l,t)-\Phi(l,t))\] 其中\(\Phi(l,t)\)表示现在长度为\(l\)的程序在种群中的占比;\(p(l,t)\)是长度为\(l\)的程序被选择进化的概率。
那么bloat极有可能发生在\(p(l,t)-\Phi(l,t)\)不为零，也就是size为\(l\)的个体选择压力和size为\(l\)的个体在当前种群中的比例不一致的时候。 根据bloat模型的分析，控制bloat的关键是在于让选择压力和个体的大小同步。根据这个理论一些方法尝试将个体大小融入到fitness function当中。这种方法潜在的问题是fitness function没有办法识别过大的个体真的是出现了代码冗余还是仅仅是因为需要拓展精度。
一些复杂的控制bloat的方式有多目标优化个体大小和fitness、重写个体为语义相等但是更小的个体等等。这些方法需要考虑，相比于让GP本身找到大小合适且fitness高的个体带来的成本和引入这些复杂机制的成本相比是否值得^[33]。

GP的模块性

自动定义函数

自动定义函数是Koza在原版GP之后提出来的一种算法，以“GP的高级功能”被引入到GP当中。一开始的ADF的理论和之后根据ADF进一步提出的理论有所不同，根据Koza在^[18]中举的Parity Code的例子，最开始的ADF应当是将已经建立好的模型作为另一个规模更大的问题的部分解，以函数的形式加入到对更大的问题的求解搜索过程中（比如4-Parity可以作为6-Parity问题的一部分）。这样的对ADF的定义是透明且可解释的。
之后的多数ADF的变体对于ADF的理解都将其与Building Block Hypothesis结合，认为由于GP根本性问题的存在，导致Building Blocks极度依赖上下文，从而有可能使得Building blocks由于在表现较差的个体中而在进化过程中消散，因此ADF的主要功能是保护有用的遗传片段，并且通过重复使用代码片段来减少冗余的搜索。
ADF并不能真正的解决GP的问题，启发式的ADF通过将某些子空间打包从而引导搜索向包含这个子空间的更高阶的子空间进行搜索，从而增加GP的运行效率。 类保护的交叉和突变也是一种限定搜索在某些子空间之内的操作。 因为在一定程度上限制了语构，进而减少了搜索过程中涉及到的语义到语构的映射数，这样的机制在一定程度上可以缓解语义和语构的映射问题。但是ADF无法从根本上厘清语义到语构的映射问题，所以也只是缓解，并没有彻底解决。

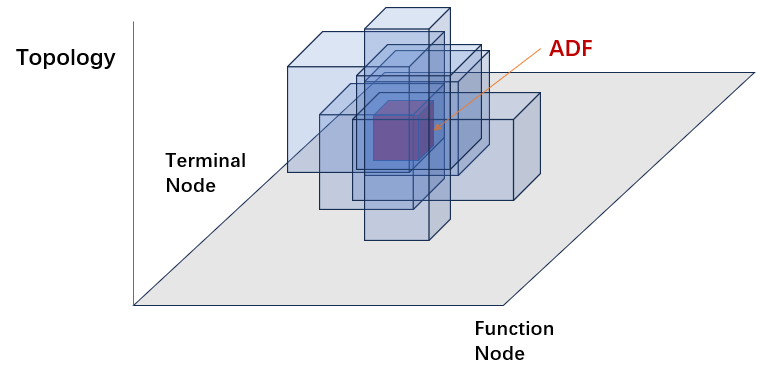
引入ADF机制之后带来了新的问题，在此总结为四点：

• 封装有用的函数
  关于如何找到有益的子树，一些工作如 AAO 中的子程序创建和模块获取（MA）中的压缩操作^[19]。 ^[19]使用随机封装，并将识别任务交给演化过程。要封装的子树是随机选择的。例如，在 Koza 的 ADF 改进版中，进化过程中的类型保护遗传操作与选择相结合，用于搜索函数中更有用的部分。 另一方面，其他关于模块化的研究都认为，需要封装对解决方案贡献最大的有益子实体，以保护这些部分免受遗传操作的破坏性影响，同时通过重复使用它们来降低复杂性。例如，GLiB ^[20]使用子程序在群体/个体中被调用的次数/频率来评估子树的贡献；Co-ADF ^[21]和 EDF ^{[22] [23]}提出了根据每个函数可能解决的适应度案例数来包含局部适应度的方法，以直接评估子树。 ^[24]在统计特征方面，^[24] 尝试应用相关性和灵敏度等统计特征来表示段的贡献。但事实证明，这两种特征并不有效。

• 防止低多样性
  群体多样性是 GP 模块化研究的另一个研究课题，它指的是搜索空间中被搜索个体的分布程度。多样性越高，说明搜索范围越广，搜索到全局最优的几率越大。问题是，多样性和模块化之间需要权衡：多样性能使 GP 避免过早收敛和局部最优，但会增加 GP 的复杂性；模块化用于降低问题的复杂性和保护有用的片段，但过强的保护效果会导致 GP 多样性降低和陷入局部最优。有几种方法认为，只有当群体缺乏多样性时，才需要对子树进行封装。基于这一观点，有几项研究集中于种群多样性的监控技术。首先，它是通过监测种群本身的特征来实现的：例如，在最初的自适应表征学习（ARL）中使用的种群熵^[25]。 该方法使用信息熵来表示种群的多样性。其次，可以通过进化过程中的一些指标来监控多样性，如 MaxFit^[24]：如果个体的最大适应度在几代内没有变化，则引入一个新模块。EDF ^[23]中也采用了类似的机制：当所有EDF的唤醒次数较低时，就会引入一个新模块。

• 类型冲突
  类型冲突通常发生在将封装的子树作为类型化系统中的函数插入到个体中时：即上层函数请求的类型与下层终端或函数的返回类型不匹配。在 ^[26]中，Koza 将约束类型作为 GP 的高级函数引入了演化过程。在这里，函数集中的所有主函数和 ADF 都有分离的终端集，其中包含类型正确的终端。虽然这种方法解决了类型冲突问题，但一些文献批评说，约束类型不仅增加了处理不同数据类型的难度，而且还增加了计算的难度， ^[27]而且还引入了更多的先验知识来为不同的函数设计不同的终端集，这与 Koza 自己的想法相矛盾 ^[28].因此，Montana 设计了强类型遗传编程（STGP）。 ^[27]其中所有元素（终端和函数）都有各自的类型。在演化过程中，将执行通过查找链接表实现的类型检查程序。此外，STGP 还引入了通用函数和通用类型。遗传函数可以对多种类型而不是特定类型进行操作。泛型类型不是数据类型，而是泛型函数支持的可能数据类型的集合。在树生成过程中，泛型被视为数据类型，但在评估过程中，由于实例化的原因，泛型被视为具体值。使用泛型的目的是消除基因运算中可能存在的非法性，同时减少对先验知识的依赖和可能存在的先验偏差（避免因指定数据类型而产生偏差）。PolyGP ^{[29] [30]}借鉴了 STGP 中参数多态性的思想，对其进行了进一步扩展，并使用罗宾逊统一算法（Robinson's Unification Algorithm）改善了 STGP 中创建个体时造成的链表结构问题，使其符合类型合法性。PolyGP 最大的变化是将 Koza 标准遗传算法中的个体表示法从 LISP 语言的 S 表达式迁移到 Lambda 微积分，并根据新表示法中 Currying 个体的结构将交叉迁移到新表示法中。这些改变使 GP 能够学习程序的结构，而不受变量和变量类型的限制。

• ADF内部进化和外部进化的协同作用
  另外，考虑到多样性和搜索的进展，如果ADF自身的内部空间也需要不断进化，比如^[21]中每个ADF有自己的独立子种群和子fitness function，那就需要考虑ADF的进化过程和整体进化过程之间的关系。在使用协同进化时，可能需要考虑在主程序进化的过程中，其function set或者是terminal set的变化对搜索过程造成的影响。

1. Z. Zojaji et al, Semantic Schema based genentic programming for symbolic regression, 2022. ↩︎
2. Z. Zojaji, M. Ebadzadeh, schema modeling for genetic programming using clustering of building blocks, 2018. ↩︎
3. Z. Zojaji, M. Ebadzadeh, Semantic schema theory for genetic programming, 2015. ↩︎
4. U-M O'Reilly and F. Oppacher, The Troubling Aspects of a Building Block Hypothesis for Genetic Programming, 1994. ↩︎
5. R. Poli et al. Exact Schema Theory and Markov Chain Models for Genetic Programming with Homologous Crossover, 2004. ↩︎
6. Forrest S. and M. Mitchell, Relative Building-Block Fitness and the Building Block Hypothesis, 1992. ↩︎
7. Whiate David Robert et al., Modeling Genetic Programming as a Simple Sampling Algorithm, 2019. ↩︎
8. O'Neill, Damien et al. Common Subtrees in Related Problems: A Novel Transfer Learning Approach for Genetic Programming, 2017. ↩︎
9. Muller, Brandon et al., Transfer Learning: A Building Block Selection Mechanism in Genetic Programming for Symbolic Regression, 2019. ↩︎
10. O'Reilly, Una-May and Franz Oppacher, Using Building Block Functions to Investigate a Building Block Hypothesis for Genetic. ↩︎
11. Goldberg,Genetic Algorithms in Search Optimization and Machine Learning, Page 41, 1989. ↩︎
12. Johnson Colin G., Genetic Programming Crossover: Dose It Cross over?, 2009. ↩︎
13. D. White, Simon M. Poulding, A Rigorous Evaluation of Crossover and Mutation in Genetic Programming, 2009. ↩︎
14. Poli, Riccardo and William B. Landon, On the Search Properties of Different Crossover Operators in Genetic Programming, 2001. ↩︎
15. George R. Price, Selection and Covariance, 1969. ↩︎
16. L.Beadle and C.G. Johnson, Semantically driven crossover in genetic programming, 2008. ↩︎
17. B.Burlacu et al, Methods for Genealogy and Building Block Analysis in Genetic Programming, 2015. ↩︎
18. John R. Koza, Hierarchical Automatic Function Definition in Genetic Programming, 1993. ↩︎
19. J. R. Koza, Evolving the Architecture of a Multi-part Program in Genetic Programming Using Architecture-Altering Operations, in Evolutionary Programming, 1995. ↩︎
20. P. J. Angeline and J. B. Pollack, The Evolutionary Induction of Subroutines, 1997. ↩︎
21. M. Ahluwalia and T. C. Fogarty, Co-evolving hierarchical programs using genetic programming, presented at the Proceedings of the 1st annual conference on genetic programming, Stanford, California, 1996. ↩︎
22. M. Ahluwalia and L. Bull, Co-evolving Functions in Genetic Programming: Dynamic ADF Creation Using GLiB, in Evolutionary Programming, 1998. ↩︎
23. M. Ahluwalia and L. Bull, Coevolving functions in genetic programming, Journal of Systems Architecture, vol. 47, no. 7, pp. 573-585, 2001, ↩︎
24. A. Dessi, A. Giani, and A. Starita, An Analysis of Automatic Subroutine Discovery in Genetic Programming, in Annual Conference on Genetic and Evolutionary Computation, 1999. ↩︎
25. J. Rosca, Hierarchical Learning with Procedural Abstraction Mechanisms,1997. ↩︎
26. J. R. Koza, D. Andre, F. H. Bennett, and M. A. Keane, Genetic Programming III: Darwinian Invention & Problem Solving. Morgan Kaufmann Publishers Inc., 1999. ↩︎
27. D. J. Montana, Strongly Typed Genetic Programming, Evolutionary Computation, vol. 3, no. 2, pp. 199-230, 1995, ↩︎
28. J. Koza, M. Keane, M. Streeter, W. Mydlowec, J. Yu, and G. Lanza, Genetic Programming IV: Routine Human-Competitive Machine Intelligence, 2003, ↩︎
29. T. Yu and C. D. Clack, PolyGP: a polymorphic genetic programming system in Haskell, 1997. ↩︎
30. C. D. Clack and T. Yu, Performance-Enhanced Genetic Programming, in Evolutionary Programming, 1997. ↩︎
31. W.Banzhaf, A. Leier, Evolution on neutral networks in genetic programming in Genetic Programming Theory and Practice III, Chap 14., 2005. ↩︎
32. Roli,R,mVanneschi,L., Langdon, W.B et al. Theoretical results in genetic programming: the next ten years?, 2010. ↩︎
33. Langdon,W.B.Jaws 30, 2023. ↩︎
34. K.Krawiec,. Opening the Black Box: Alternative Search Drivers for Genetic Programming and Test-based Problems, 2017. ↩︎