Geometric Semantic Genetic Programming：基于几何信息的GP

Alberto et al., Geometric Semantic Genetic Programming, PPSN, 2012.

Alberto Moraglio, Krzysztof Krawiec, Semantic Genetic Programming, GECCO, 2019.

Alberto Moraglio et al., Geometric Semantic Grammertical Evolution, 2018.

背景

传统的GP重视语构(Syntax)而轻视语义(Semantics)，然而对于GP的树形结构，非常小的对树形结构的调整都有可能引起相当大的语义的改变。如果将fitness视作是个体的语义并且用schema theory进行估计，同一个schema中过大的fitness差别导致schema theory*无法非常准确的预测schema在其后的采样率变化。

*： 此处的schema theory指的是GA式的Pessimistic Schema Theory.

反过来，如果从语义上归置schema，也就是具有相同语义的个体是是一个schema。并且将GP的搜索过程，也就是Genetic Operator的作用对象从结构换到语义，那么这个对Schema扩散的建模会更加清晰，并且语义决定了一个个体的表现是否会被Selection淘汰或者继续存活，因此语义才是决定搜索质量的关键。从这个角度出发，作者认为GP的搜索过程应当在语义而非语构上进行。 现有的在语义上的Genetic Operator设计普遍采用的模式是“Generate-Reject”。即先用Genetic Operator产生后代，然后再检查后代的语义是否在指定的范围内，如果不再则不承认此次操作的结果。这种方法存在两个问题：1.大量的计算资源被浪费 2. 这种方式起到的唯一作用只有限制搜索，并没有有效建立起genetic operator与语义之间的联系。

几何语义的GP

语义的搜索

现在假设存在一种衡量GP个体语义的方式。定义一个个体是一个函数\(h:X \rightarrow Y\),属于某个类\(H\)，这个类是函数\(h\)所使用的全部Primitives。对于训练集\(T=\{X,Y\}\)有\(\forall (x_i,y_i)\in T:h(x_i)=\hat{y}_i\)，定义\(O(h)\)是个体在训练集\(T\)上的输出向量：\(O(h)=(h(x_1),h(x_2),...,h(x_N))\)，那么函数\(O:H\rightarrow \hat{Y}\)可以表示为一种函数\(h\)的结构组成到函数\(h\)的行为之间的映射关系，即表现型和基因型的映射。

传统的对于个体的表现衡量的方式是基于个体的输出和目标之间的差值。作者对个体到目标在fitness的差的理解是：这个差值在fitness的空间中表现为个体的fitness与目标fitness之间的语义距离，用距离函数可以表示为：\(D(Target,O(h))\)。根据具体任务的不一样，距离函数\(D\)可以是海明距离，欧氏距离和曼哈顿距离等等。那么两个个体之间表现的差异也可以通过距离来衡量，对个体\(h_1\)和\(h_2\)，有其表现的差异为\(D(O(h_1),O(h_2))\). 在许多时候\(h_1\)和\(h_2\)虽然不同，但是\(O(h_1)\)可能与\(O(h_2)\)相同，如果一个语义值可以算作是一类，那么定义具有相同表现的个体同属于一个语义的schema \(\overline{H}\)，此时\(D\)可以视为是对个体属于哪一个语义schema的衡量函数。如果存在语义的交叉和语义的突变，由于所有的操作都是在语义上完成的，所以这样的操作的实际对象是语义的schema，因此结果也应该是语义值，这个值通过生成一个满足这个输出表现的个体来实现语义schema的实体化。

如果抛弃对语义的冗杂定义，最简单而直接的对语义的定义就是个体的fitness，而fitness则是个体的表现到目标输出之间的误差。如果把这个fitness直接作为距离，那么语义搜索的fitness landscape则是一个锥形，顶点为目标，锥形的每一个\(x-y\)方向的切面都是一个语义的schema \(\overline{H}\)。

语义的操作

设计的操作算子需要满足设计的crossover和mutation在基因型和表现型上的一致性：对基因型的遗传操作需要与表现型相对应。

交叉

作者在此处借用了逻辑选择，认为语义交叉生成的后代应当同时保留两个亲本的行为，并且通过某种方式来调整两个亲本在后代上的表现，从而实现原来标准交叉中的部分继承。这样的语义交叉可以被视为是如下的条件选择函数，后代则是这个函数的结果。那么在不同的问题上面这样的交叉操作可以总结为下表：

问题	语义交叉函数	表现	使用到的距离衡量函数
逻辑回归	\(Offspring=(T1∧ TR)∨(T2 ∧ \overline{TR})\) \(TR\)是一个随机生成的布尔函数	\(Off=\begin{cases}T1,TR=1\\ T2,TR=0\end{cases}\) 即一个Multi-plexer函数，后代一定在\(T1\)和\(T2\)海明距离的中间，这种交叉语义上具有和GA的交叉相同的性质，见下面的例子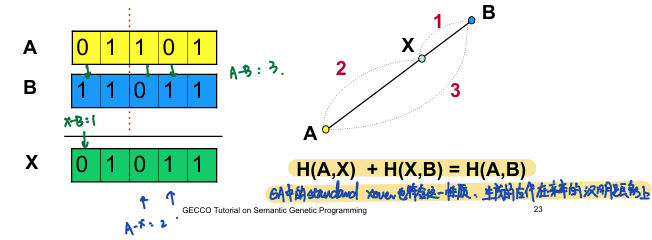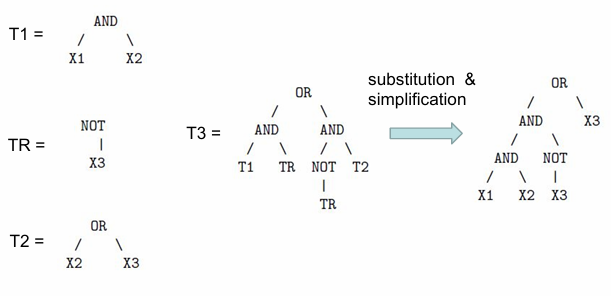：	海明距离
代数回归	\(Offspring=(T1·TR)+(T2·(1-TR))\) \(TR \in[0,1]\)是一个随机数	\(Off=\begin{cases}T1,TR=1\\ (T1·TR)+(T2·(1-TR)),TR \in (0,1)\\ T2,TR=0\end{cases}\) 即Multi-plexer函数在实数域上的表现，此处用到了凸组合(convex combination)的数学性质：系数满足之和为1的线性组合称为凸组合。对于二元凸组合：\(k=(1-t)v_1+tv_2,t\in[0,1]\)，凸组合的结果\(k\)一定在\(v_1\)和\(v_2\)的连线上。	欧拉距离
程序设计	offspring = IF CONDER THEN t1 ELSE t2 CONDER是一段随机生成True或者False的程序	>> t1 when CONDER == True t2 when CONDER == False	海明距离

不管是何种问题，在确定的距离度量下，GS Genetic Crossover的基本思想（也可以说是结果）交叉产生的后代必然在亲本连线上。由于Fitness Landscape是锥形的，此法产生的后代的语义表现必然优于其中一个亲本。

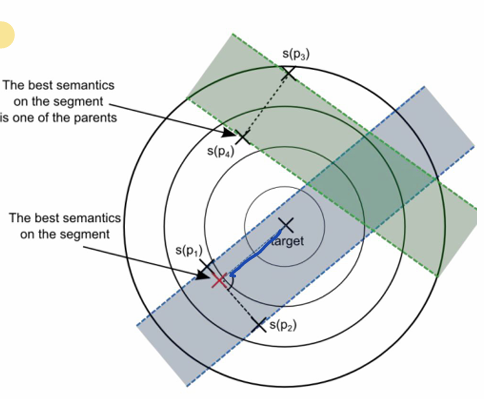
后续的几种GS crossover的改进有：

• Krawiec and Lichocki Crossover

  要求后代不仅在亲本的连线上，而且最小化后代和亲本之间的语义差异 \(min||s(z)-s(p_1)||+||s(z)-s(p_2)||\)。但是这种方法非常容易找到与其中一个亲本语义相似的后代，为了避免这种情况，后续的改进是增加了一项优化两个亲本到后代的距离之差也使其最小：

  \[min||s(z)-s(p_1)||+||s(z)-s(p_2)||+min||s(z)-s(p_1)||-||s(z)-s(p_2)||\]

• Subtree GS Crossover

  原版的GS Crossover生成特定的某种语义表现的GP树个体在有时候会特别困难，但是如果是生成某个特定语义值的子树可能会简单一些。因此Krawiec和Pawlak提出了Locally Geometric Crossover：具体的操作是：

  1. 在Common Regions中查找交叉点
  2. 计算这两点之下子树的语义并且找到中值
  3. 在库中找到语义相似的子树并且嫁接到两个亲本上

  

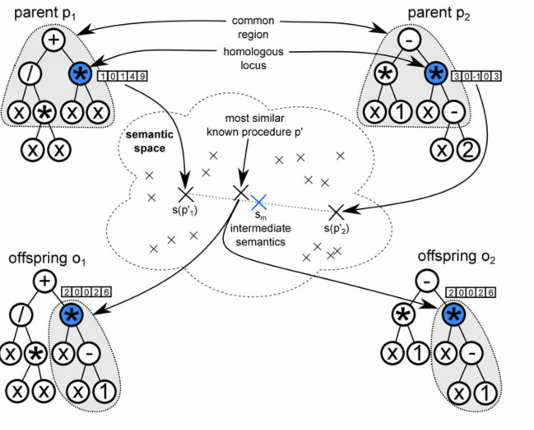
突变

突变的想法是基于现在亲本的语义值，让这个语义值在空间上发生在某个范围内的变动。

问题	语义突变函数	备注
逻辑回归	\(Offspring = \begin{cases} T ∨ M, r\geq 0.5 \\ T ∧ \overline{M},r<0.5\end{cases}\) \(r\in[0,1]\)为一个随机数
代数回归	\(Offspring = T+ms·(TR1-TR2)\) \(ms\)为步长，\(TR1\)和\(TR2\)为两个随机生成的函数（且语义之差小于某个非常小的范围，近似于0）	这个过程潜在地模拟了bloat的相互抵消的过程
程序设计	offspring = IF CONDER THEN outr ELSE t outr是随机生成的一个符号。

GSGP的这种突变方式在语义上会表现为GA的mututation：

程序大小控制

以上的交叉和突变在结构上由于继承了亲本的全部结构，因此不可避免地个体的大小会越来越大，事实上，个体大小的增长几乎呈现指数形式。为了解决这个问题，原版的GSGP中在进行完genetic operator后需要进行逻辑或者是数值化简，程序在化简前后的语义不会发生任何变化。化简的目的是保证genetic operator可以在比较小的size上积累有效信息，本质上是一种浓缩有效信息的方法。

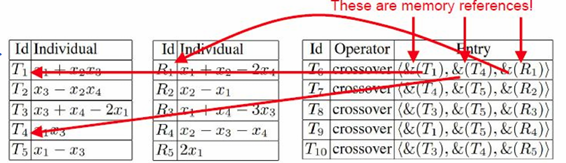
在后续的版本中，由于数值化简的兼容性和计算复杂度，这种方法被弃用。在Tiny GSGP(Vanneschi el al, 2013) 中使用了一种链表的方式: 个体以显性链表数据结构表示，指向父代兵递归指向所有祖先，由于每一代中每个新的交叉后代只需要引进一个新的子树，因此计算复杂度和个体大小的增长都是线性的。

实际实现的方式是通过Python的匿名函数以及装饰器特性：

在Tine GSGP中，所有的个体的基因型都是以匿名函数的形式存储的，crossover通过拼接字符串的方式将亲本p1和p2的匿名函数拼接为后代的匿名函数并且保存：

def crossover(p1,p2):
    """
    交叉操作符是一个高阶函数，它接收父函数并返回子函数。
    子代函数的定义中不会替换父函数的定义。
    而是从子代函数中调用父函数。这样可以防止指数增长。
    """
    mask = randfunct()
    offspring = lambda *x: (p1(*x) and mask(*x)) or (p2(*x) and not mask(*x)) # 此处的*x表示不考虑输入变量的数量，就是*args
    offspring = memoize(offspring) # 加入缓存
    # 拼接后代的匿名函数
    offspring.geno = lambda: '(('+ p1.geno() + ' and ' + mask.geno() + ') or (' + p2.geno() + ' and not ' + mask.geno() + '))' 
    return offspring

在 crossover 函数中，memoize 记录了 子代函数 offspring 计算过的输入及其对应的输出，即 输入-输出映射，以避免重复计算。memoize 用于给 offspring 添加缓存，存储已经计算过的输入值及其对应的输出结果。

def memoize(f):
    'Add a cache memory to the input function.'
    f.cache = {}
    def decorated_function(*args):
        if args in f.cache: # 如果输入已经出现过，直接从缓存中取结果，避免重复计算
            return f.cache[args]
        else:
            f.cache[args] = f(*args) # 如果是新的输入，则计算并存入缓存
            return f.cache[args]
    return decorated_function

在进化过程中，offspring.cache会以{(input keys):output,}的方式存入evaluation的结果，比如：

offspring.cache = {
    (True, True, True): False,
    (False, False, True): False,
    (False, False, False): False
}

当 offspring 再次被调用时：

• 如果输入已经出现过，直接从缓存中取结果，避免重复计算。
• 如果是新的输入，则计算并存入缓存。

几何语义GP的发展版本

GSGE

GSGE是将GSGP和语法进化(Grammertic evolution)结合的方法。GSGP的genetic operator具有可组合性：结构上组合表达的语义和各个子结构表达语义后的组合后的语义是相同的。而GE中的基因型和表现型映射的设计也是一种可组合的设计，因此作者尝试将GS genetic operator翻译为GE可以接受的函数形式，使其在GE上也可以工作。

在GE中，用户需要自己规定语法，语法相当于标准GP中的terminal set和function set。语法库中每一个语法按照类别进行了大小类的编号，不同类中的元素的编号可以相同，相同类中的Primitives的编号必须不同，类的编号也必须不同，如此就可以根据编号准确的定位到某一个特定的Primitive。个体的基因型是一串编号序列，表示了如何按照顺序选取语法然后构建这个个体。这个编号序列按照从左到右，从上到下，深度优先的方式遍历树生成。个体的语构，称为衍生树，通过按照这串序列描述的选取语法构建树的顺序来构建。

如果基因型已被耗尽，⽽衍⽣尚未完成，则将“包装” 索引到基因型的开头。或者，在基因型⽤尽之前，衍⽣可能已经完成。在这种情况下，多余的基因被简单地忽略了。

个体的表现型则是衍生树在所有可能取值上的表现所组成的向量。

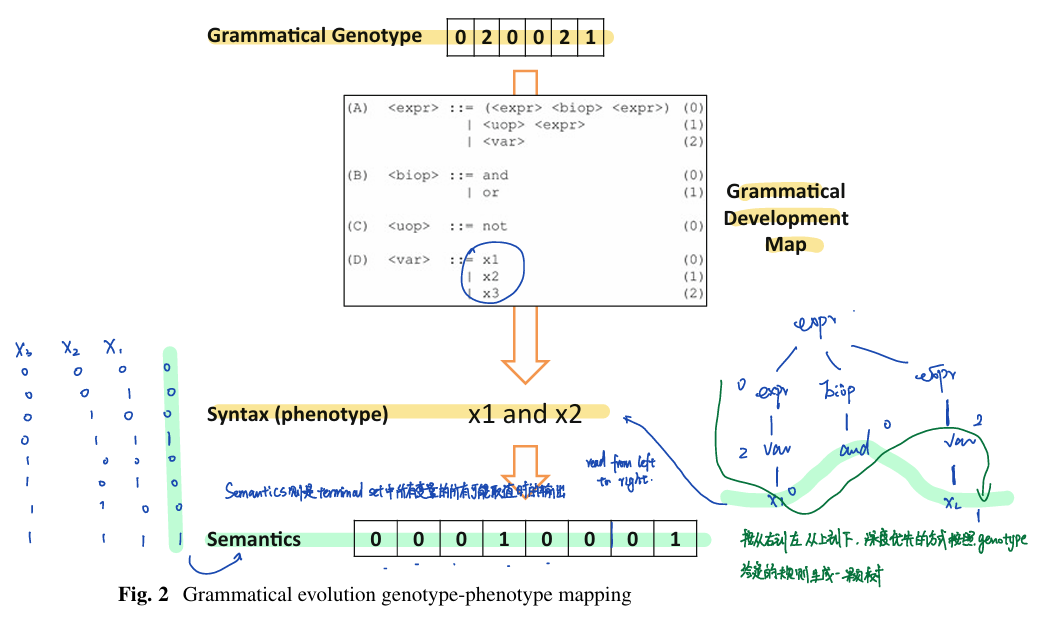
此处GE有几个特性：

• 基因型到结构的转换是可逆的

• 深度优先展开的方式让基因型和表现型的映射是以模块化的方式进行的：结构上的子树在基因型中对应的是连续的一块区域，因为深度优先算法会将一个子树表示完成之后再表示下一个子树。因此，可以在基因型上将一块特定的子树打包，以函数的方式存放在基因型中。

  

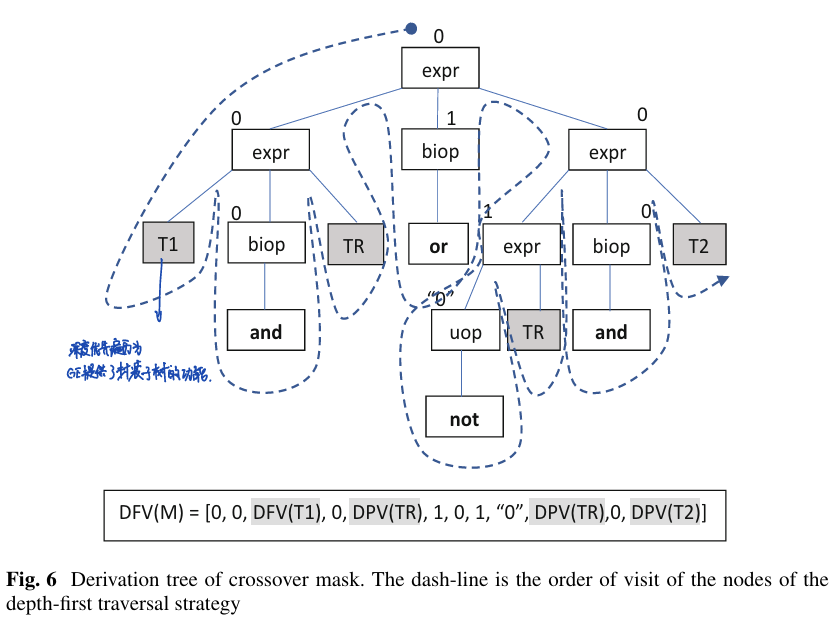
因此，GS的genetic operator在GE中可以表现为一颗树，这个树的某些部分以亲本\(T1,T2\)和mask\(TR\)填充即可。并且通过这种模块性的方式，交叉作为一个函数可以实现层级调用，“后代的后代”可以递归调用“后代”的交叉函数，如此个体的基因型长度将始终恒定保持不变。

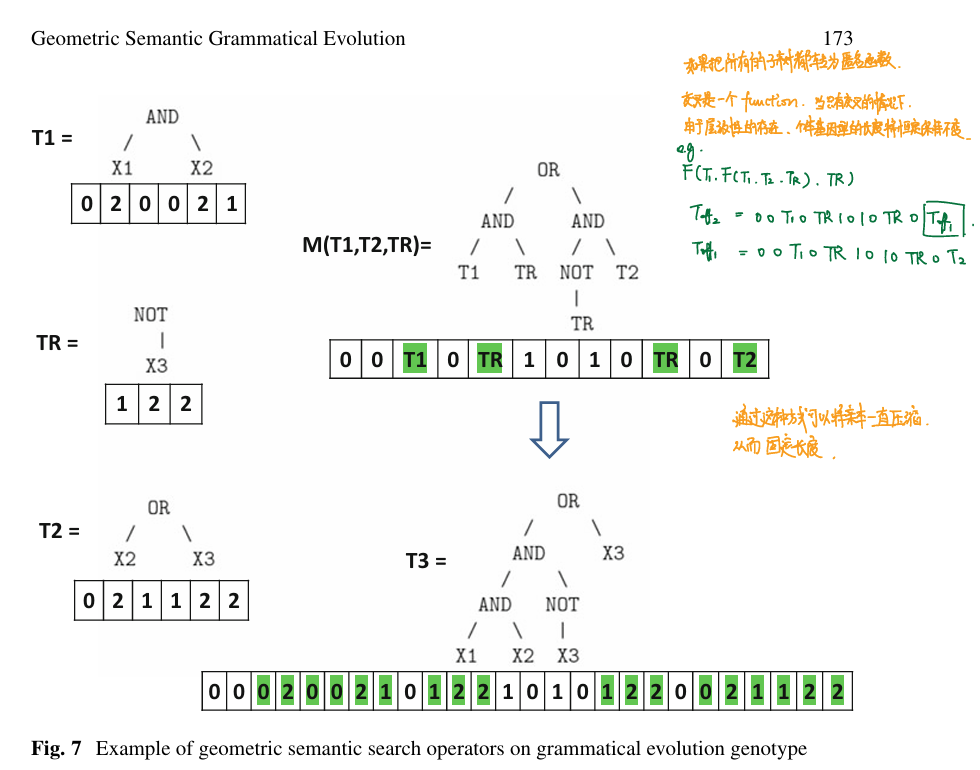
结构重要吗？

GSGP的作者认为从理论上来说，结构不重要(In theory, it does not matter./ Remark 3: Syntax Does Not Matter !)，因为后代纯粹地由其功能所定义。在实际上，结构是重要的(In practice, syntax does matter!, 在GECCO的presentation中没有对结构是重要的描述)，个体的结构会影响种群初始化的方式，因而影响初始语义的分布。并且crossover mask的形状会影响后代的哪个部分由哪一个亲本决定。

个人认为，结构对进化的影响可能要大于GSGP作者的想象。结构是遗传信息的载体，Evolutionary Algorithms通过结构上的继承和组合来存储已经搜索到的遗传信息。事实上正是因为genetic operator（不论是GA还是GP）是一种作用于结构的搜索方式，而通过个体的设计，结构上的连续对应在fitness域上不连续的表现（这种不连续的表现在GA中是可以控制的），Evolutionary Algorithms才具有全局性。

但是也不能否定局部搜索方式进行的GP的有效性，GSGP巧妙的一点是距离=误差的定义让fitness landscape变为锥形，在这个空间中理论上不存在局部最优解，因此局部搜索的方式在这样锥形的空间中的搜索或许还要比全局式的搜索更快。