遗传编程中Evolvability的进化

Lee Altenberg. 1994. The evolution of evolvability in genetic programming. Advances in genetic programming. MIT Press, Cambridge, MA, USA, 47–74.

介绍

在GA中，Gentic Operator和Representation的选取会对GA的性能产生很大的影响，其原因是因为Genetic Operatior和Representation包含了同一个过程的两个方面：从旧的搜索空间中创造新的elements。这个问题可以通过evolutionary approach创建可以进化的representation和operator来让GA自己演化（多臂赌博机问题的进化采样分配问题）。这一篇论文将介绍Genetic Programming(GP)也具有进化自身的representation的能力，并且介绍representation的进化方向是如何影响整个个体的可进化性的(evolvability)。

可进化性

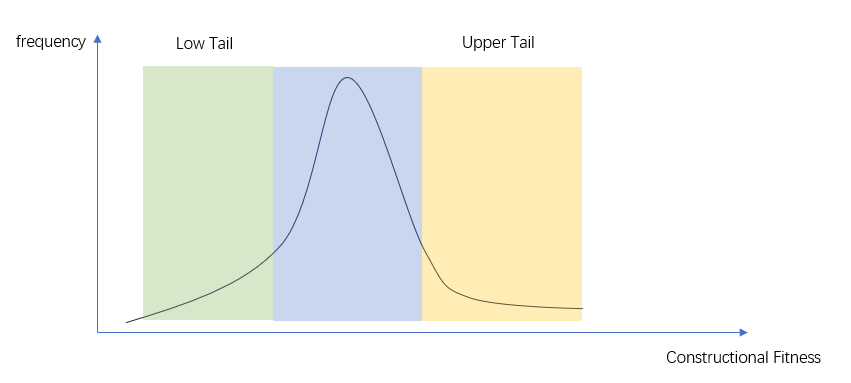
可进化性(evolvability)指的是Genetic Operator或者是Representation产生的后代优于自身的概率。定量的定义是Genetic Operator或者是Representation所产生的后代的概率分布。对于进化计算而言，具有好的“evolvability”的定义是其产生的后代的fitness分布的上分位点区域应当比随机搜索的fitness分布更宽。但是和随机搜索相比，“产生适应度更高的后代”这种行为不一定会在所有亲本中出现，它只需要发生在高于平均fitness的亲代身上，因为选择的偏置效应会让搜索进程偏置到这些亲本的方向上。综上所述，更高的evolvability意味着更好的亲本有更高的概率产生更好的后代。即理想的operator要在亲本和后代的fitness表现中产生相关性。
“相关性”的定义可以通过Building Block Hypothesis展示：亲本中隐含的遗传信息通过交叉传入后代，使后代的fitness提升。所以building blocks的定义应当有亲本和后代fitness在交叉下产生的关系而建立起来。
Evolvability是一个非常局部，或者说非常细粒度的对GA（或者说进化计算）的性能的测量指标（因为是从某个后代开始推理的测量指标）。由于种群整体的进化方向是全局的没所以只要GA可以保持evolvability，那么最终整个GA的表现将会是全局的。

表现

GA中的Evolvability通过genentic opeartor作用于representations（individual，注意这是94年的论文），让representation保持其高度适应的部分的同时扰乱还没有高度适应的部分。更细化的来说，Representation上要完成两个维度上的目标，这里用热水龙头的例子来进行类比：
水龙头对热水温度和水量的控制有两种方法：

1. 两个水龙头，一个水龙头控制冷水的出水量，另一个水龙头控制热水的出水量。
   
2. 一个水龙头，x-y轴旋转控制水温，z轴旋转控制出水量。

显然第一种控制方式更难控制热水的水温（目前我家里就是这种，烫的要死）。受控对象的可控维度更高更容易控制。或者说，第二种方法的表示的控制维度和问题解答的维度是相同的。（一个representation上的控制维度为2，和目标问题的维度相同。）GA的基础设计任务也是这样——设计一个系统让representation的变化尺度和任务的变化尺度匹配。那么在GP上，任何一个个体都是其行为的结构表示，同一个行为具有不同的程序结构，每一个程序结构都拥有不一样的evolvability，其中有一些结构的representation拥有更强的evolvability，经过genetic operator修改之后可以产生适应度更高的后代。
在定长表示的GA中，selection的作用对象是Population，而不是representation。GP则同时作用于这两种。

已有尝试

GA中对evolvability进化和控制的尝试包括：

• 用allelic value来控制genetic operator
• Genetic Operator的parameter设置也具有fitness
• 让operator专注于产生了适应度更高的后代的个体
• 调整mutation opeartor来维持fitness distribution的分布
• 不同的bloack of code的扩散速率不同

Constructional Selection

GP中个体片段扩散的关键在于representation和其duplicates之间存在结构上的相似性。重组可以作用于这些duplicats上任何一个位置的片段。由于片段的可复制性，GP达到了Dawkins提出的涌现的第一个阈值：level of replicator。由于选择直接作用于个体，让个体成比例地复制，因此个体是GP中replicator的基本层级单位。
如果genetic operator可以增加“可以高概率产生适应度更高后代”的个体片段的采样率，那么整体的evolvability就会提升。个体片段的采样率提升即个体片段实例化数量的提升（注意这里对building blocks的考虑位置关系与否有争议，因此文章中避免使用building blocks一词，而使用piece of code。因此每个个体可以拥有多个相同的代码片段，后面GEP book中也提及到最佳的个体中往往有重复出现的building blocks，因为GEP的building blocks可以具有位置无关性），可以通过如下的两种方式实现：

• 通过增加携带这个片段的携带者的数量（schema thoery）
  这种方式无法让程序片段在同一个个体中出现多次。“但是，这种纯粹的选择效应并不能在程序中产⽣更多的代码块拷⻉。 这就需要通过将更多的代码拷⻉从供体程序插⼊到受体程序中来创造新的程序。 如果后代程序存活的时间⾜够⻓，它们就会成为更多程序拷⻉的接受者，或者被⽤作捐献者，向其他接受者程序捐献更多的代码拷⻉。”
• 通过多个有这个片段的个体与同一个个体进行交叉：
  
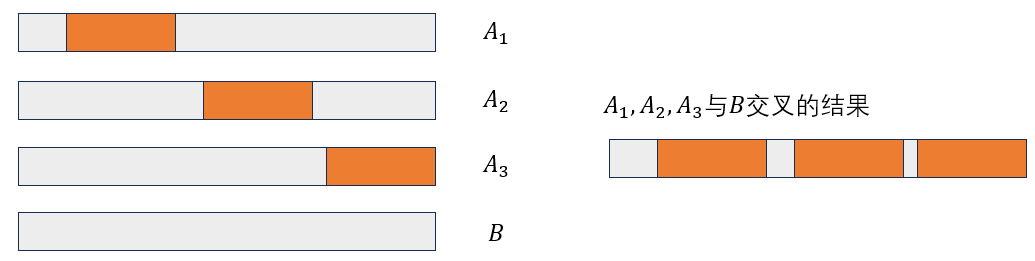
  Schema Thoery并没有考虑这一种情况，因此不同的代码片段的扩散速度依赖于重复地使用不用的代码片段替换而产生的fitness的统计差异。

如果block of code对其实例化的个体的fitness分布有非常稳定的影响（后续对于语义和语构的研究表明这在标准GP中是非常困难的），那么其在个体内部的扩散速率可以定义为Constructional fitness。
那么是什么决定了Constructional fitness？如果将GP的piece of code的在个体内部的扩散过程视为是一种爬山效应：将个体内部一个位置的piece of code复制到同一个个体内部的另外一处进行修改，如果修改的结果导致适应度提升则保留，如果不行则舍弃。这样的描述类似于自然界的gene duplication：对于不好的同个体的复制则会在下次有机会通过crossover之前被移除，因此只有有利的同个体复制会被保留下来。此时piece of code的扩散将会完全依赖于constructional fitness，genentic operator会将可能更容易产生fitness更高个体的piece of code进行扩散。
那么定义piece of code的evolvability value为其加入一个个体后可以使个体产生适应度更高的后代的概率。可以发现，piece of code的扩散依赖于个体的存活时长。在高crossover rate时，更高evolvability value的piece of code不需要contructional fitness也可以非常快地在个体内部进行扩散。与此同时，即使一个在选择下即将消失的个体也可以被genetic operator多次采样，成为新个体的贡献者之一，自然而然地，其上的bad effect也有机会通过genetic operator转移到其他个体上。在这种情况下，对后代产生中性效应的piece of code的constructional fitness会比“bad effect but on good individual”的piece of code更高，从而避免了顺风车效应。
从evolvability的角度来看GP的动态性，在进化前期，种群中的一个piece of code要想存活的话，其在种群中的扩散改进个体表现的速率要大于种群平均的fitness改进速度。在此阶段，piece of code竞争的是改进个体的速度；在进化的后期，piece of code的主要任务是让一个适应度高于平均的个体不要受到genetic operator的disruptive effect的影响。在此阶段piece of code竞争的是鲁棒性。如果将结构距离比作关系性强度，那么结构越紧凑（信息密度越大）的schema越容易存活。

数学建模 - GA

这一小节主要是对GA中evolvability的进化速度进行了数学建模。

传递函数

对进化计算算法的数学建模开始于对transmission function的构造：即用数学语言描述genetic operator对representation的作用： \[T(i ← j,k)\] 表示为亲本\(j,k\)产生后代\(i\)的概率。
有Tranmission function和fitness function之间的关系决定了GA的性能。Transmission Function用于进一步筛选fitness function的作用效果，因此fitness的影响只能通过transmission function传递给GA的搜索。在Genetic operator的作用下，亲本和后代之间的关系对GA表现的影响是重要的：如果不存在这样的关系，那么选择筛选到的亲本的优势将无法传递给后代。
根据普莱斯公式，\(j,k\)后代的平均表现可以写作：
\[φ_{jk}=\sum_{i}F_iT(i←j,k)\] 其中\(F\)称为测量函数，表示的是某个个体的某种量化性质，譬如适应度。
根据普莱斯公式，整个种群的下一代表现写作： \[\overline{F'}=\overline{\varphi}_u+Cov[φ_{jk},\frac{ω_jω_k}{\overline{ω}^2}]\] 其中\(ω_j,ω_k\)为\(j,k\)的fitness。
\[\overline{\varphi}_u=∑_{jk}φ_{jk}x_kx_j\] 其中\(x_j,x_k\)是选择\(j,k\)作为亲本的概率，即\(j,k\)的采样率。
根据定义，那么亲本表现和后代表现的关系，即普莱斯公式中的协方差一项，有：
\[Cov[φ_{jk},\frac{ω_jω_k}{\overline{ω}^2}]=\sum_{jk}φ_{jk}\frac{ω_jω_k}{\overline{ω}^2}x_jx_k-\overline{φ}_u\]

测量函数

现在定义测量函数为： \[F_i(ω)=\begin{cases} 0, ω_i≤ω\\ 1, ω_i>ω \end{cases}\] 即如果个体的fitness大于某个阈值\(ω\)，则返回1，否则为0. 那么有：
\[\overline{F}(ω)=\sum_iF_i(ω)x_i=∑_{i:ω_i>ω}x_i\] 现在定义搜索偏置(search bias)\(β_{ij}(ω)\)为\(jk\)产生的后代的fitness高于\(ω\)的概率，那么有：
\[β_{ij}(ω)=∑_iF_i(ω)T(i←j,k)-\mathclose{R}(ω)\] 其中\(R(ω)\)表示随机搜索可以找到个体fitness高于\(ω\)的概率。
可以发现\(β_{jk}(ω)\)可以视为是亲本配对\(j,k\)的evolvability。
整个种群的平均search bias为：
\[\overline{β}_u(ω)=\sum_{jk}β_{jk}(ω)x_jx_k\] 那么下一代fitness高于\(ω\)的采样率表示为：
\[\overline{F'}(ω)=\underset{随机搜索产生的}{\mathclose{R}(ω)}+\underset{交叉产生的}{\overline{β}_u(ω)}+\underset{选择产生的}{Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]}\] 当\(\overline{F'}(ω)>\mathclose{R}(ω)\)是，证明GA并不是随机搜索算法，此时\(\overline{β}_u(ω)+Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]\)一项应该为正。
这一项为正有两种情况：

• \(Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]<0\)且\(Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]<\overline{β}_u(ω)\)
  • \(j,k\)的fitness相对于平均越来越高，但是不能产生足够的fitness高于\(ω\)的后代，这种情况在收敛时会发生。在这种情况下\(Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]<\overline{β}_u(ω)\)。
    
  • \(j,k\)的fitness相对于平均越来越低，但是可以产生足够的fitness高于\(ω\)的后代，这种情况几乎不可能发生。

上述的这些公式并不需要与schema的概念链接。Schema Thoery中并未对GA在哪些问题中的难易程度作出分辨。但是Building Blocks hypothesis的框架中，隐含的意思是，在crossover的作用下，这⾥的定理中给出的回归项和搜索偏差项将是正值。在欺骗性问题和其他很难解决的遗传算法问题中，在种群进化过程的某个阶段，即在找到最优之前，可进化性会消失，即这个式子会归零或归于零以下。
例如，使用8421编码的 GA 中的单个比特变化会导致字符串编码的实值参数发生巨大变化，这个问题称为hamming cliff，因为参数空间的巨大跃迁会降低相关性，从而无法解决典型问题。格雷码平均提高了单个比特变化产生的相关性。

exploration 和 exploitation

现在让这个公式的粒度再细一些，来区分transmission function对现有种群的挖掘(exploitation)和探索(exploration)程度，对任何transmission function，其可以改写为：
\[T(i←j,k)=\underset{采样到自己作为亲本的概率}{(1-α)}(δ_{ij}δ_{ik}/2)+αP(i←jk)\] 其中\(α\)表示的是非“自交”的最大概率，即最大的exploration概率：
\[α=1-\min_{i,j≠i}\{2T(i←i,j),T(i←i,i)\}\] \(δ_{ij}\)表示的是对\(i\)的内部进行搜索：
\[δ_{ij}=\begin{cases} 1,i=j\\ 0,i≠j \end{cases}\] transmission function中的exploration部分为\(P(i←j,k)\)，称为search kernel。
那么一个个体后代的采样率可以写作：
\[x_i'=\underset{exploitation}{(1-α)\frac{ω_i}{\overline{ω}}x_i}+\underset{exploration}{α∑_{jk}P(i←j,k)-\mathclose{R}(ω)}\] 最大的evolvability将出现在\(α=1\)时，但是此时\({(1-α)\frac{ω_i}{\overline{ω}}x_i}=0\)选择将停滞。
令\(ω=ω_{max}\),\(ω_{max}\)为当前种群中的最大fitness，已说明GA搜索到比既有的fitness更高的后代的概率。\(ω>ω_{max}\)意味着出现了既往从未有过的新个体，对这个个体的exploitation的概率为0，那么有：
\[\overline{F'}(ω_{max})=\{\mathclose{R}(ω_{max})+\overline{β}_u(ω_{max})+Cov[β_{jk}(ω_{max}),\frac{ω_jω_k}{\overline{ω}^2}]\}\] \[β_{jk}(ω_{max})=\sum_iF_i(ω_{max})P(i←j,k)-\mathclose{R}(ω)\] 下一代种群的evolvability（evolvability的进化）可以写作：
\[\overline{β}_u'(ω)=∑_{j,k}β_{jk}(ω)x'_jx'_k=(1-α)^2[\overline{β}_u(ω)+Cov[β_{jk}(ω),\frac{ω_jω_k}{\overline{ω}^2}]]+O(α)\]

上述所有理论适用于任何表示方案和遗传算子，这一点非常重要，因为它们提供了判断表示方案和算子的标准。在某些表征下，突变可能会在搜索空间中带来更大的可演化性；而在其他表征下，重组或其他算子可能会带来更大的可演化性。
因此，对于譬如实数编码的GA之类的其他表示类型或者是变种的genentic operator的GA只要在整个进化过程中可以达到和标准GA相同的evolvability，都可以视为是合法的GA变种。

GP的evolvability

现在来看GP，block of code在种群中的扩散是基于它们在添加到个体上时对其fitness分布造成的影响结果造成的。不同的block of code的扩散会导致genetic operator产生的对fitness的效应\(β\)发生改变，从而改变evolvability。

block of code的contructional fitness

在前面的章节中提到过，在高crossover rate的情况下，中性的block of code和有害的block of code相比时扩散更具有优势。在低crossover rate的情况下，有害的block of code通常在它们可以被扩散之前就已经消失了。更极端的情况是，如果只有好的block of code可以crossover扩散出去，那么GP具有最明显的爬山效应。
下面的推理将基于如下的假设：

• block of code的扩散是离散的，而不是相互嵌套的
• block of code添加到个体之后对个体的影响是稳定的

定义block of code的表现型是block of code对个体fitness改变量的概率分布，block of code \(k\)在添加到个体\(j\)后产生个体\(i\)的fitness大于\(j\)的适应度\(ω_j\)的概率可以写作：
\[ξ_k=∑_iF_i(ω_j)P(i←j,k)=β_{jk}(ω_j)+\mathclose{R}(ω_j)\] 这个式子可以理解为对于个体\(j\)，添加一个block of code\(k\)之后fitness得到改进的概率。
继续化简这个式子，假设block of code对其附属的每一个个体的影响程度都是恒定的，\(ξ_k\)可以认为是这个block of code的contructional fitness.
令\(n_i(t)\)表示type \(i\)在第\(t\)代的某一个个体中的数量，\(i\)被选择的概率为：
\[p_i(t)=n_i(t)/N(t),N(t)=∑_in_i(t)\] \(N(t)\)是整个个体中所有的block of code的总述，可以反映个体的大小。
那么对\(n_i(t)\)求导，表示block of code的扩散概率为：
\[\frac{d}{dt}n_i(t)=\underset{exploration发生的概率和改进成功率的乘积}{αξ_i}n_i(t)/N(t)\] 那么有两个block of code在程序中的扩散速率的比值呈现指数上升：
\[\frac{n_i(t)}{n_j(t)}=\frac{n_i(0)}{n_j(0)}e^{α(ξ_i-ξ_j)∫_0^tdτ/N(τ)}\] 现在推广到整个个体，对于整个个体中所有的block of code，其平均contructional fitness可以表示为：
\[\overline{ξ}(t)=∑_iξ_ip_i(t)\] 同样地对其进行求导：
\[\frac{d}{dt}\overline{ξ}(t)=\sum_iξ_i\frac{d}{dt}(n_i(t)/N(t))=\frac{α}{N(t)}Var(ξ)\] 其中\(Var(ξ)=[∑_iξ_i^2p_i(t)-\overline{ξ}(t)]\)，表示contructional fitness的方差，代表多样性。那么根据上式，某个个体的evolvability的增长速度与多样性成正比，与个体大小成反比。
可以发现，evolvability提升的关键是genetic operator作用于现有的个体上，让其产生适应度更高的个体。

讨论

constructional selection

在高crossover rate的进化后期，鲁棒的block of code会比最大提高fitness的block of code更受欢迎，因此constructional fitness与block of code的扩散程度并不是对应关系。这是因为高crossover rate的重组总是会对constructional fitness分布的中间和上分位部分起到选择作用。随着种群适应度的提高，上分位（constructional fitness高）的部分会缩小，因此平均适应度将成为比constructional fitness更重要的统计量。
在低crossover rate的进化中，constructional selection会选择更高constructional fitness的block of code。
以下提出了几种在高crossover rate下根据constructional fitness进行选择的方法：

1. 只保留比亲本更好的后代，甚至成倍地复制这些后代
2. 亲本交叉若干次，只保留最好的个体作为真正的后代
   • 这种方法和1相比不会改变后代的数量

这两种方法会增加上分位和下分位的block of code的数量。

理论的应用

Representation和operator的变化仅仅通过它们对transmission function的改变来关联到进化过程的动态性。在GP上，representation即是fitness function的作用对象，用于复制新个体，也是genetic operator的作用对象，用于产生变化。也就是说，GP的representation具有生成和变化两方面作用，但是只有representation的变化作用会与进化过程的动态性相关。
两种对GP的representation的改变的例子是Module Aqusition和ADF。对于ADF，GP的operator对ADF所作用的过程相当于是同时对主程序中出现该ADF的位置进行变化，这一过程相当于识别了重复出现的block of code并且对其进行修正。对ADF的进一步修改的版本试图将ADF的可改变维度和问题的维度进行对齐：

• 让某些ADF出现的位置替换为其实例，以便于进行更细致的调整。（但是这样做会让整个个体的结构产生大规模形变）
  
• 让ADF在每个被调用的位置都拥有一定的自由度，进行非统一的变化。
  
• 交叉发生在ADF区域的子树的根部和分支的边界上，如此对ADF的输入将保持不变。
  
• 允许子树的返回值被多个子树复用。
  
• 单步解决，让个体在小规模的fitness cases上达到要求后再给它更大规模的fitness cases。