12. 进化成分分析

这是对《Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence》的笔记，本页对应第12章： Chapter 12： Evolutionary Studies 本书可以在斯普林格购买纸质版或者电子版：https://link.springer.com/book/10.1007/3-540-32849-1

本章利用各种控制变量的实验研究GEP中各部分对整体进化性能的影响。

Genetic Operator的作用

进化在整体上依赖遗传变异，并伴随着某种选择。然而，进化计算学界仍对创造遗传变异的最佳方式在突变和重组之间意见不一。事实上，人工进化系统自身也在进化，在不同的表征方式的掩饰下，可以事先的简单的复制系统和基因型/表现型系统。所有这些系统的遗传修饰机制都与它们的表示方法错综复杂地联系在一起。 我们已经看到，GEP不仅使用突变和重组，还使用不同类型的易位，因此，如果可以对不同搜索算子的性能进行严格的分析，以深入了解它们在进化中的作用将对GEP的进化机制有更深层次的了解。我们将看到，突变是迄今为止最重要的遗传算子，其性能远远优于重组。事实上，本文分析的三种遗传重组（单点、两点和基因重组）的性能都远低于突变，也远低于简单的染色体内易位。此外，我们还将详细分析所有这些遗传算子产生的进化动力学，以了解它们在进化中的重要性。
作者在这一章中做了一个简单的符号回归实验，在这个符号回归实验中，每个实验只打开一个Genetic Operator并绘制出Operator Rate和Success Rate（运行100次能够准确找到最优解的频率）之间的关系折线以探究它们对进化的影响，结果如下图所示。

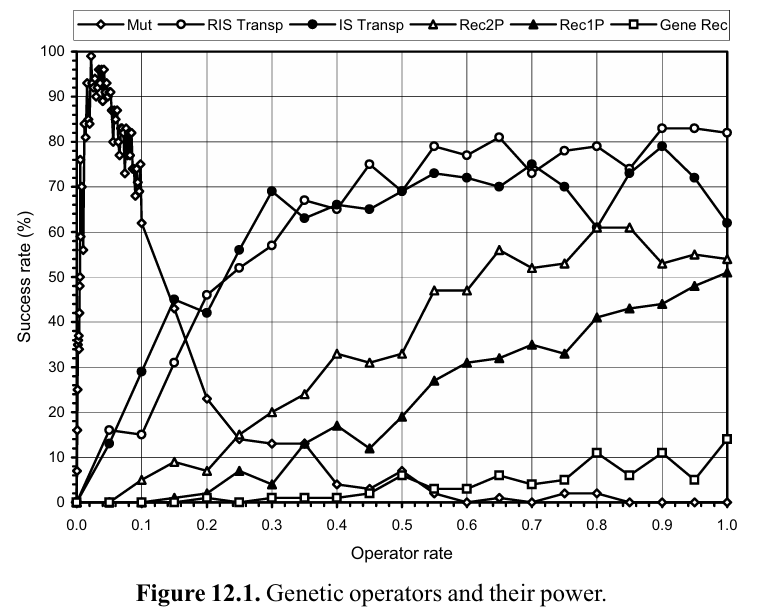
如上图所示，所有的Genetic Operator的Performance排序结果如下:
突变(Mut)>RIS Transpose>IS Transpose>重组(Rec2P,Rec1P,Gene Rec)
可以发现，一方面重组的Success Rate非常高，另一方面三种重组机制(Rec2P,Rec1P,Gene Rec)的Success Rate明显低于其他的Genetic Operator.

• 如果单看突变，可以发现突变随着突变概率的提升的性能表现和其他的Genetic Operator相比非常不同。而且，经历突变的系统可以很容易地进行调整，使得种群能够保持在顶峰(接近100的Success Rate)，尽管通过上图可以发现突变率的微小变化会在上图的指状区域内产生巨大影响，因此这种顶峰是不稳定的。
  突变具有巨大的创造力，事实上，仅凭这一算子就足以演化出几乎所有问题的解决方案。尽管如此，出于实践和理论原因，其他遗传算子可以并且经常在GEP中使用。例如，RIS Transpose就很有趣，因为它挑战了我们对进化中过度修改重要性的看法。此外，众所周知，突变的创新性不足以解释自然界的所有进化现象。
  
• 两个Transpose的表现相比于突变更差，比重组更好，其中RIS transpose的表现略优于IS Transpose。因为RIS Transpose会改变子树的根节点，因此造成的disruptive效应会比IS Transpose更强。
  
• 对于重组：
  两点交叉是三个交叉算子中disruptive最大的，在单独使用它时是最有效的。
  保护性最强的是基因交叉。但是此处的GEP系统中即使是最保守的基因交叉，其发生的概率和操作仍然比自然界的同源交叉更为激进。作者认为，这些更加保守的重组机制只有在进化的停滞期才会有助于维持现状。

从上面的分析可以看出，GEP中具有disruptive效应越强的算子由于持续不断地在进化过程中添加新的遗传物质，在合理的范围（允许进化系统自适应的范围）内其distruptive效应的增大会带来进化效率的提升。

不同设置下种群表现出的动态性

之后，作者继续分析了上面实验过程中每一个Operator Rate下种群的Average Fitness和Max Fitness随着代数的变动情况。
在进一步的分析中，作者主要看了图中的如下特征：

• Max Fitness和Average Fitness的最终值：最终性能
  
• Max Fitness和Average Fitness的差异，在图中差异越大暗示了种群的多样性越高，Max Fitness和Average Fitness重合意味着种群中所有个体的fitness都是Max Fitness，此时种群的多样性非常低。
  
• Average Fitness的振荡，Average Fitness曲线振荡越剧烈代表着种群的结构变化越快，意味着种群的多样性非常良好。

下面展示了不同的突变概率下种群所展示出来的动态性：

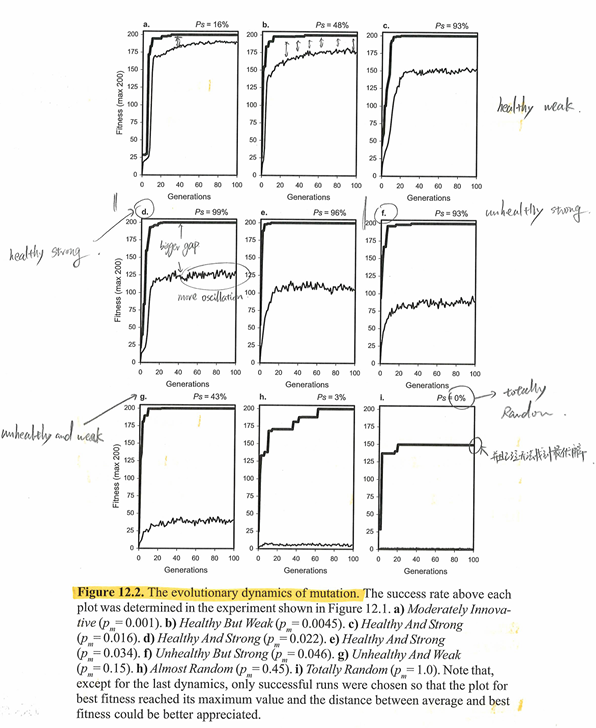
该实验的结论如下：

• 对于突变，在指形区域内随着突变概率的提升，Fitness Max和Fitness Average的差距越来越大，表示种群多样性的提升，Average Fitness曲线的振荡也说明了这一点。但是随着突变概率越来越高，种群越来越难以进行适应，搜索会越来越趋向于随机化。\(p_m=1\)的搜索性能非常差，这表明随机搜索并不具备找到完美的解决方案的能力，因此之前实验中每次找到完美的解决方案都是由于强大的搜索机制所造成的。
  
• Transpose展示出的动态性和突变比较相似，RIS Transpose Rate为1时的表现比IS Transpsoe Rate为1时的表现更好。但是和突变不同的是，无论在何种Rate下Transpose可以始终保持Average Fitness曲线的剧烈震荡。
  
• 所有的重组算子都展示出同质化的趋势：Average fitness会越来越靠近best fitness，最终闭合。这样的现象表明只依赖于重组来进化的种群的多样性会越来越低，并且在大多数时候提前收敛。总体上重组算子的Average fitness曲线的振荡都非常小，但是其中高crossover Rate带来的振荡比低Crossover Rate带来的振荡更大，这表明高Crossover Rate下收敛所需要的时间更长。GEP中的重组不会引入新的基因，重组的作用在不断的尝试组合已经挖掘的遗传物质。它更重要的作用是维持现状，从而让进化体现出持续性。

但是在另一方面，系统的性能不仅会随着突变率而发生显著变化，而且性能峰值仅靠突变即可达到。因此，可以轻松调整突变率，从而使系统以最高效率进化。事实上，突变率本身受到严格控制，并受到自然界选择压力的影响，这再次表明，突变，而非重组，才是进化爆发的中心。 最后，我们还观察到，Transpose表现出与突变类似的动态（即异质化动态性），并且经历Transpose的种群进化得比仅经历重组的种群更好，这进一步强调了重组独特的同质化效应。

综上所述，可以发现GEP的遗传操作可以分为两类：
一类是通过引入了新的遗传物质、或者是大范围地更改基因的操作，譬如突变和Transpose，这些操作会让种群的多样性升高从而让种群中的个体彼此越来越不同，这样的操作称为异质化操作。
另一类是通过尝试旧的遗传物质的组合来实现小范围更改基因的操作，比如重组，重组不会引入新的基因，并且在动态性上倾向于让种群的多样性降低，这样的操作称为同质化操作。

此处GEP的交叉表现出和GP交叉完全不一样的结论，原因和GEP/GP的个体表示以及遗传信息有关，详见下面的讨论。

初始种群

前面的章节中已经展示出来，系统的可进化性将在很大程度上取决于用于创建基因改造的遗传算子的类型。初始种群的规模和种类与此问题密切相关。
在所有进化算法中，一个进化周期或运行都始于一个初始种群。然而，初始种群的生成方式多种多样，不同算法的性能和成本（以 CPU 时间计算）很大程度上取决于初始种群的特征。
最简单、耗时最少的初始种群是完全随机的初始种群。然而，很少有进化算法能够使用这种初始种群，这不仅是因为结构上的限制，还因为可用于创建基因改造的遗传算子的类型。
相比而言，GEP的初始种群是完全随机的，由种群中个体的线性基因组组成。
在进化计算中，初始种群对进化计算的影响可以简述为如下的推理：
由于初始种群产生的大量个体都是不可达的，因此初期的进化过程会极大地依赖于对可达个体的改进。那么Genetic Operator就非常的重要，如果Genetic Operator可以引入新的遗传物质，那么对新区域的搜索得以继续进行；如果不能引入新的遗传物质，那么最终解的质量只能由初始种群的多样性决定。在此定义为初始种群中那些可达的个体称为奠基者(Funder).
在生物学中将初始多样性在进化中由于遗传漂变引发的奠基事件，并随后受到自然选择而建立的新种群的效应称为Funder Effect。Funder Effect的一个极端情况是，一只怀孕的雌性生物在一片先前无人居住的地区定居。在自然界中，除了基因重组之外，其他遗传算子也被用于创造变异，突破瓶颈的种群能够适应环境，有时甚至会衍生出新物种。
同样，在人工进化系统中，初始种群的进化能力很大程度上取决于用于创造遗传变异的机制类型。事实上，如果同质化算子是遗传变异的唯一来源，那么在只有一个奠基个体的极端情况下，种群将无法有效进化，甚至根本无法进化。因此，同质化操作为唯一来源的进化系统中，初始种群的多样性和sucess rate有明显的关系。
对于异质化的操作，初始种群的多样性和sucess rate并没有明显的关系，因为异质化的操作会持续的引入新的遗传物质，因此理论上总会找到最优解。
需要注意的是，种群大小越大进化过程消耗的计算资源越多。因此，像GEP这样能够以最小的初始多样性高效进化的系统极具优势。此外，对于一些复杂问题，随机生成一个可行个体，甚至一个平庸的个体来启动运行都非常困难。在这种情况下，像 GEP 这样的系统可以将这个个体作为创始个体并从那里继续运行，而仅依赖于重组的系统则会在积累动力之前停滞很长时间。事实上，在GEP中，由于存在一组非同质化的遗传算子，因此不需要大量的创始群体，因为只要随机生成一个可行个体，进化过程就可以开始。

Building Blocks Hypothesis

上面的几个小结已经说明，如果进化系统只依赖于现存的building blocks来挖掘关联关系，其性能会严重地受到限制。这一个小结的实验中将探索三个系统：一个系统不断在种群中引入变异，以及两个不同的系统，它们只能重组一种特定的building blocks——GEP基因。回想一下，GEP基因具有明确的边界，通过基因重组和Transpose，可以在不破坏这些building blocks的情况下测试它们的新组合。

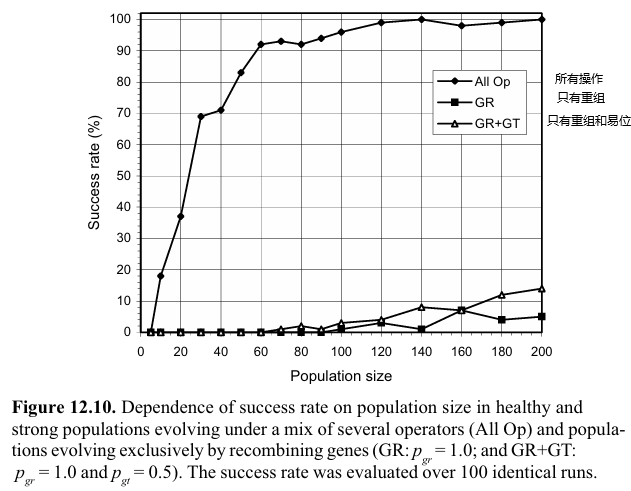
实验发现，无法持续向基因库中引入新遗传物质的系统进化得较差。
此外，如果building blocks只是移动，或者说调整位置关系，而没有以某种方式被破坏，系统实际上无法进化。只有使用相对较大的种群，才有可能解决这个简单的问题，尽管效率非常低，尤其是在只能移动building blocks的情况下。不过，现实世界的问题比这里分析的问题复杂得多，因此，应该始终使用更强大的搜索运算符，例如突变。
总而言之，移动building blocks对进化的影响有限：如果没有突变（或其他非同质化运算符），适应过程会非常缓慢，并且需要大量个体，因此效率低下。

自然映射

只有在拥有真正的基因型/表现型的情况下，计算机程序的自动进化才能顺利高效地完成。这一小节将探究基因型表现型映射为GEP这样的人工进化系统所带来的优势。
和自然界的遗传一样，GEP中也有基因型和表现型的二元表现，其次基因型必须可以产生有效的表现型。在GEP中，这两个与自然进化相似的特性是通过引入非编码区段来实现的。
自然界的遗传系统中，基因是以区段的形式存放在DNA上，其次有相当多不表现的DNA，称之为Junk DNA。GEP模仿了自然界中的基因分段和Junk Sequence这两个特性。正如前面章节所述，中性突变的积累在进化中起着重要作用。而 GEP 染色体的非编码区正是中性突变积累的理想场所。
中性突变的积累在GEP中有两种方法可以实现，在单基因系统中，可以通过增加基因长度的方法来增加非编码区域；在多基因GEP中，则可以通过增加非表达的基因的数量来增加不表现的基因。
接下来的内容中，作者进行了一组对比试验来分析基因组中中性区域的重要性，从而分析中性突变在进化中的重要性。

单基因系统的冗余

在第一个实验中，作者探究了单基因系统中染色体长度和Success Rate在两个问题中表现的关系。

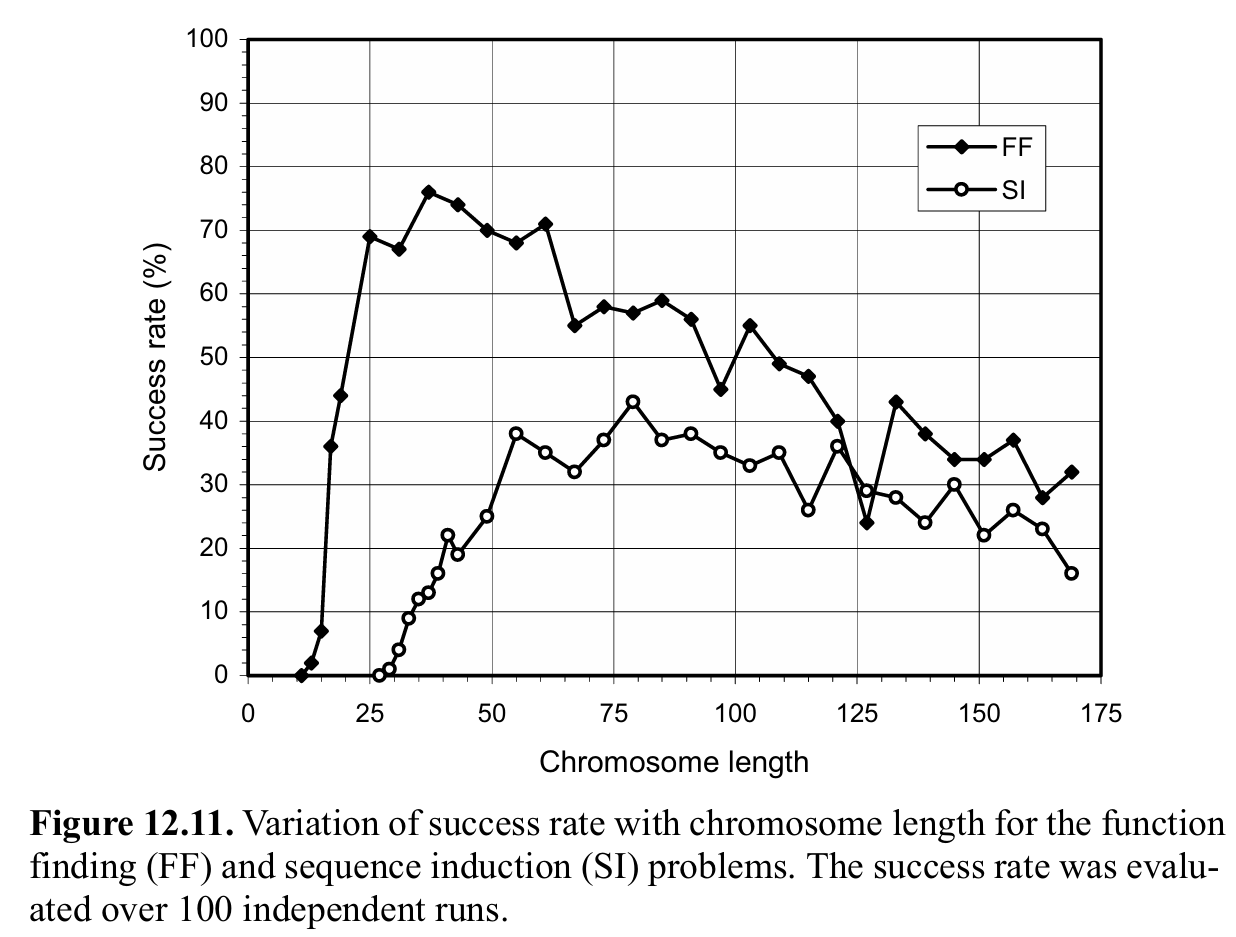
结果发现，GEP在找到表现好且简介的个体后，基因长度的增加会带来更加不简洁的解，此时相互抵消的blocks（称为中性的blocks）和非编码区段都可能会出现。从图上可以看到，在FF问题中，最紧凑的组织（染色体长度为13）的成功率仅为 2%，而染色体长度为 37 时的最高成功率为 76%。在SI问题中，也观察到了相同的现象：最紧凑的组织（染色体长度为29）的成功率仅为 1%，而最佳染色体长度（染色体长度为79）的成功率高达 43%。
上述结果表明，个体并不是越简单越好，一定程度的冗余对于高效进化至关重要。事实上，在这两个例子中，都发现了一个平台期，系统在此阶段进化得最好。另外，高度冗余的系统适应能力明显优于高度紧凑的系统，这表明进化系统能够很好地应对遗传冗余。
再来进一步分析单基因个体的最优解的结构，可以发现这些最好的个体中都出现了大量的非表示区段以及多的中性block。也就是说，这些最优个体都发生了bloat。但是，通过这个实验表明，与所有类型的遗传冗余一样，中性序列在适度使用时很可能是有益的。这可以通过基因表达编程进行严格的评估，尽管这样的分析需要大量时间。

多基因系统的冗余

接着，作者探究了多基因系统中基因数量和成功率在两个问题上的关系，结果如下图所示：

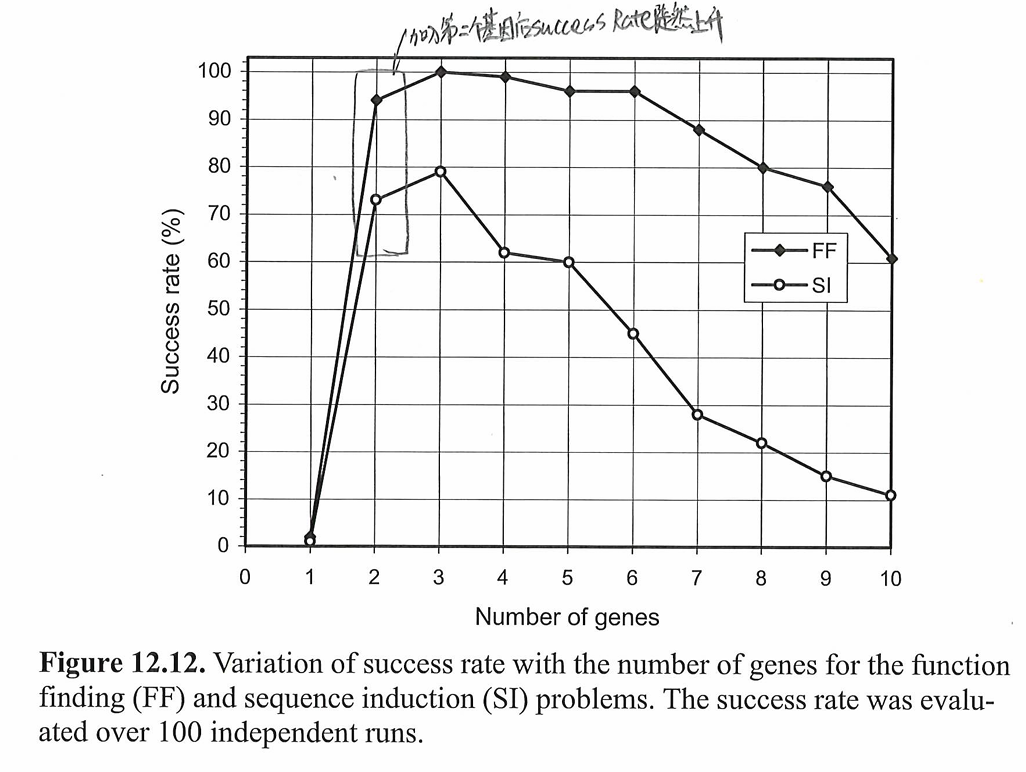
当第二个基因加入到系统中时，进化系统的成功率突然上升。不紧凑的多基因的表示可能比紧凑的单基因GEP更加有效。但是基因的数量并不是越多越好。
现在种群中如果一定的表示空间（不仅是通过构建新的building blocks，也可以是通过抛弃现在找到模块）对发现新的解至关重要，如果没有足够的表示空间，那么只有通过高代价（更长）的个体来解决问题。因此冗余的系统表现比紧凑的系统更好。

现在综合而言，可以推断出非编码区段对于进化的两个作用：

• 保护有效信息不会受到genetic operator的扰乱
  
• 隐含地积累有效信息，但是不表现出来
  
• 让Genetic Operator永远合法

在GEP中，冗余基因有两种方式可以实现，第一种是ORF（表现型）中的中性blocks，第二种是ORF后面的非编码序列。GA和GP只有第一种方式而缺乏第二种方式。
上述实验说明了中性序列产生了结构的多样性，其允许重组在相同的语义上测试不同的buildingblocks，同时让进化可以创建最终可以分化为更适应的结构的变体。

另外，作者还进行了在相同染色体长度上多基因和单基因系统的表现，结果发现多基因在大多数情况下应当成为首选。但在有些问题上，比如最终解中包含有\(log\)或者根号时，多基因可能不会那么有效，但是即使在这种情况下GEP也有自动将不必要的基因转化为中性基因的方法，并依然会找到最优解。

选择机制

为了探究不同选择机制对GEP的影响，作者对比了三种选择下GEP的性能：

• 锦标赛
  随机的选择若干个个体，其中最好的个体产生一个后代，重复这个步骤直到达到种群大小。
  
• 确定性选择
  在确定性选择方案中，个体的选择与其适应度成比例，而适应度较低的个体将根据设定好的排除引子\(E\)排除。排除因子E为1.5似乎在大多数情况下是最佳折衷方案。每个个体占有的选择几率表示为：
  \[\frac{f_i}{\overline{f}}\times E\] \(E\)越大表现好的个体就更容易占据有限的个体位置。

实验发现三者结果非常接近，细看锦标赛的结果略次于确定性选择和轮盘赌。不过全书使用的都是轮盘赌而不是确定性选择，理由如下：

• 现实世界的问题比本文分析的问题更为复杂。
• 理想的排除因子取决于种群规模和问题的复杂性。
• 确定性选择需要更多的CPU时间，因为必须按等级对个体进行排序。
• 确定性选择不会显著降低种群的遗传多样性。
• 轮盘赌选择易于实现，并且更忠实地模拟自然，因此更具吸引力。

讨论：重组

在本书中，作者对GEP的重组在进化计算中的性能有诸多质疑。Building blocks Hypothesis以及交叉的重要性在GP的研究领域中被反复强调。那么此处为何会得出和GP不一样的结论？个人认为关键在于GP的标准交叉并不是一种对位交叉，其破坏程度要大于GEP的对位交叉（虽然GEP的对位交叉也不是同源交叉），因此在交叉过程中GP对关联关系的扰乱量要比GEP可能要大得多。因此，此处对于重组过于保护性的说法可能在GEP中更为突出。
在树的粒度上，building blocks包含两种信息，一种是语义表现，另一种是位置信息。GP上的非对位交叉毫无疑问地会改变同一个building blocks的位置信息；但是GEP上的对位交叉尽管可能会导致表达区段和非表达区段的相互转换，但是其始终只会改变少量的元素的语义（试想一下在GEP的线性结构上发生一次单点交叉，那么最多只会让一个基因发生变化），与此同时，不管交叉后的部分是否表现，这一部分和其他部分在染色体上的相对位置关系始终没有发生变化。综上所述，GP的交叉和GEP的交叉不能一概而论。GP的交叉所产生的结果要比GEP的交叉更为复杂。
说到底，根本原因还是因为GP没有区分基因型和表现型，交叉在树形结构上的结果会直接反馈给个体表现。